t分布を用いた検定

検定とは

第8回で示したように，母数は標本からある程度は推定することができます． しかし，標本のサンプル数$n$が少ないときは， 標本分散から母分散を推定することは難しくなります． このため，前回学んだ 標準正規分布を用いた検定（Z検定） を適用することができません．

• 母平均$\hat{\mu}$は標本平均$\mu$で推定できる
• 母分散$\hat{\sigma}^2$は標本分散（不偏分散）$\sigma^2$で推定できる

そこで，利用するのがt検定です． t検定では，母分散の推定値に，標本分散を用いて検定を行います． すなわち，母分散$\hat{\sigma}^2$が未知の場合です． このような場合は，t分布 と呼ばれる正規分布によく似た釣鐘状の分布を利用します． 今回は，t検定 の基本を解説した上で，R言語の関数を利用した検定を行います．

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します． 次に，[ファイル]-[保存]をクリックして，スクリプトを保存します． このとき，ファイル名はchapter10としてください． また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

t検定

具体例として，前回と同じ問題を取り上げていきます． 前回と異なるのは母集団の分散が未知というところです．

上記の問題を t検定 で考えます． 準備として，標本の分散を求めておきましょう．

x <- c(63,75,72,67,71)
> var(x)
[1] 21.8

母集団は「文化情報学部の学生$X$」， 標本は「向研究室に所属する学生$x$」と考えることができます． また，「標本平均の分布」を$m$とします． いずれも正規分布に従うと仮定すると，母集団の分布と，標本平均の分布は下記のようになります． ここで，母分散$\hat{\sigma}^2$は未知であることに注意してください．

$X \sim N(60,\hat{\sigma}^2)$

$m \sim N(60,\hat{\sigma}^2/5)$

帰無仮説 と 対立仮説 は前回と同じです． 信頼区間も前回と同じ「95%信頼度（5%棄却域）」を用いることにしましょう．

• 帰無仮説：標本（向研究室に所属する学生）の母平均$\hat{\mu}$は60である
• 対立仮説：標本（向研究室に所属する学生）の母平均$\hat{\mu}$は60ではない

それでは，t検定の検定統計量であるtスコアを計算します． tスコアは下記の式で求めます． この式は前回と同じですが，標本平均の標準偏差$\acute{\sigma}$の算出方法が異なります．

$t = \frac{\mu - \hat{\mu}}{\acute{\sigma}}$

母分散$\hat{\sigma}$が未知のため， 標本平均の標準偏差$\acute{\sigma}$は下記の式で求めます． ここで，$\sigma$は，標本の標準偏差 です（Z検定では母集団の標準偏差$\hat{\sigma}$を用いた）．

$\acute{\sigma} = \sqrt{ \sigma^2 / n }$

• 標本の標準偏差$\sigma=\sqrt{21.8}=4.67$
• 標本のサンプル数$n=5$

上記の式を基にtスコアを計算します．

> t <- (69.6 - 60)/ sqrt(21.8 / 5)
> t
[1] 4.597566

tスコアは4.59という結果になりました． ここで，前回は標準正規分布を利用して棄却域に含まれるかを判断しましたが， 今回は t分布 の出番です． t分布は正規分布とは異なり，自由度 という概念があります． 自由度はt分布の形を決めるパラメータであり， ここでは$n-1=4$を自由度に設定します（詳細は割愛します）．

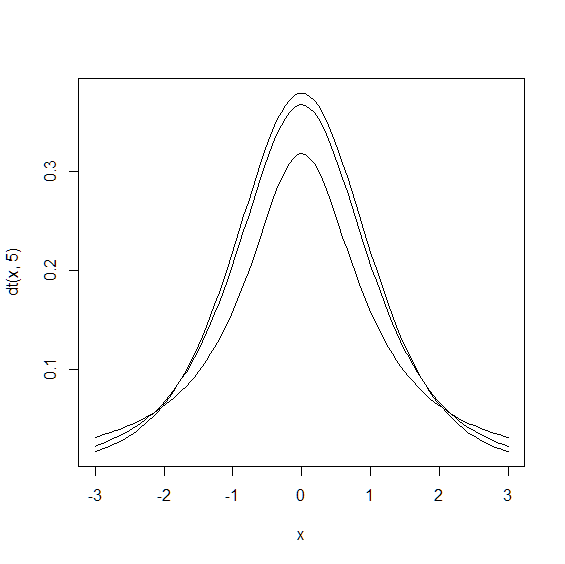
ここで，自由度 が1，3，5のt分布のグラフを描いて，その形状を確認してみましょう． t分布の確率密度を算出するにはdt関数を用います．

> curve(dt(x,5),-3,3)
> curve(dt(x,3),-3,3,add=TRUE)
> curve(dt(x,1),-3,3,add=TRUE)

自由度が大きいほど，尖った形状となり，峰が高く裾が低い形状になります． また，自由度が無限大に近づくと，t分布は正規分布に一致します． この場合，サンプル数が増えるほど，正規分布に近くなり，Z検定と同じ意味になるということです． よって，サンプル数が少なくても多くても t分布を適用すれば間違いない です．

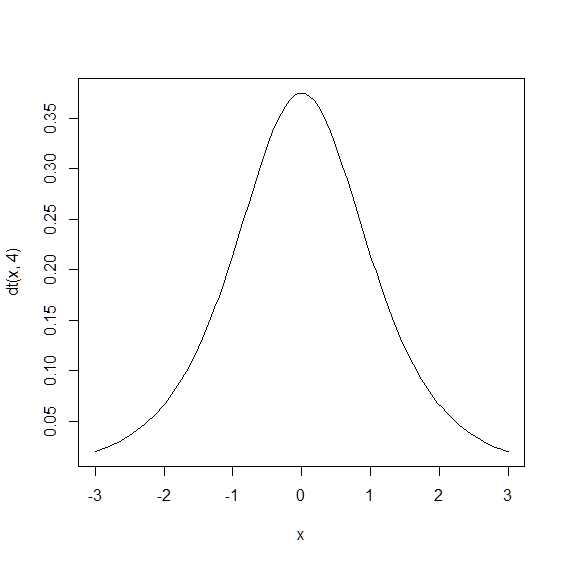
さて，問題に戻ります． 今回は自由度が4のため，下記のt分布に従います．

> curve(dt(x,4),-3,3)

この分布を利用して，先程求めたtスコアが棄却域に含まれるかを確認しましょう． ここでは，5%棄却域を採用するため，下側確率 が0.025， 上側確率 が 0.975となるtスコアを探します． tスコアを求めるにはqt関数を利用します．

> qt(0.025, 4)
[1] -2.776445
> qt(0.975, 4)
[1] 2.776445

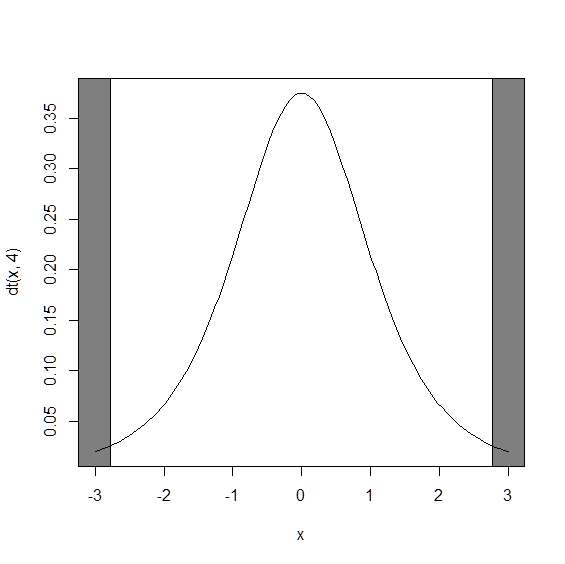
上記より，t<-2.77，また，t>2.77 となる確率は5%ということが分かります． これは，下図の左端と右端のグレーの範囲を表しています．

今回の標本のtスコアは4.59だったため，棄却域に含まれ，その確率は5%以下であるということが分かります． よって，前回と同様に，帰無仮説（向研究室に所属する学生の母平均は60である）は棄却され， 対立仮説（向研究室に所属する学生の母平均は60ではない）が採択されます．

また，このときの母平均$\mu$の95%信頼度の信頼区間は，下記のように求めることができます． 信頼区間の意味は前回を参照してください．

$-2.77 < \frac{69.6 - \mu}{\sqrt{21.8 / 5}} < 2.77 = 63.81 < \mu < 75.38$

関数を利用したt検定

R言語では，t検定を行うためのt.test関数があります． 使い方はとても簡単で，引数に標本$x$と， 母平均$\hat{\mu}$を設定するだけです．

> t.test(x,mu=60)

		One Sample t-test

data:  x
t = 4.5976, df = 4, p-value = 0.01005
alternative hypothesis: true mean is not equal to 60
95 percent confidence interval:
 63.80261 75.39739
sample estimates:
mean of x 
	 69.6 

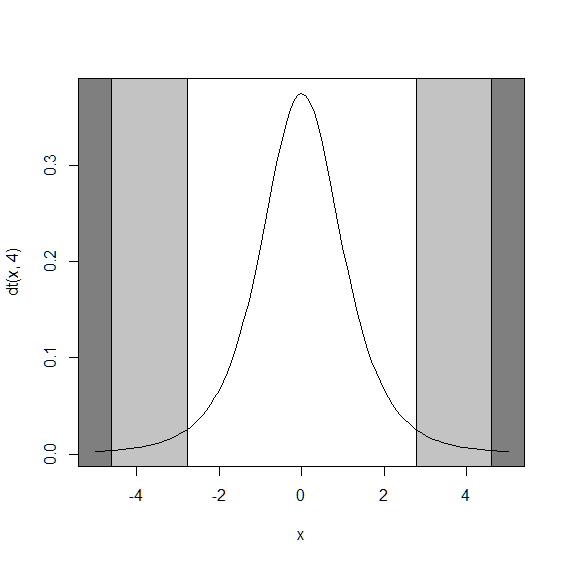
実行結果を確認すると，tスコアが4.59であることが分かります． 同様に，自由度を表すdfは4と表示されています． また，p値の0.01005（1.005%）はtスコアに対する累積確率（今回は両側の）を意味しており， p値 < 0.05(棄却域) である場合に帰無仮説は棄却となります． p値の2分の1のパーセント点を確認すると-4.59となり，絶対値がtスコアと一致します． 下図においては，薄いグレーが5%の棄却域であり，濃いグレーが1.005%の棄却域です．

> qt(0.01005/2,4)
[1] -4.597475

また，母平均の95%信頼度の信頼区間は63.80から75.39となっており，誤差はありますが先程求めた値と一致します．

課題

向研究室の学生の得点が{65,55,52,45,51}だったときのtスコアを求めなさい． また，t検定を用いて，「95%信頼度（5%棄却域）」のときに， 「帰無仮説：標本の母平均$\hat{\mu}$は60である」は棄却されるか調べ，そのときの母平均の信頼区間も求めなさい． ソースはchapter10.Rに記述して提出すること．

参考書籍