母集団と標本

母集団と標本

統計の醍醐味の一つが「推測統計」です． 推測統計では，対象となるデータが大規模であるために，その一部を取り出したデータから推測するということを行います． このとき，対象となるデータ全体のことを母集団，取り出した一部のデータのことを標本といいます． 例えば，日本国民全体の平均身長を調べるためには，莫大な費用と時間がかかってしまいます． そこで，多少の正確さは犠牲にして，一部の国民を対象として調査し，全体を予測するということが現実的な方法です． ここでは，母集団が正規分布であると仮定して，母集団と標本の関係を明らかにしていきます． これからは，ある母集団（または標本）$X$が， 平均$\mu$，分散$\sigma^2$に従うとき， 下記のように表記しますので注意してください． ここで，$N$は，Normal Distribution（正規分布）の頭文字です．

$X \sim N(\mu,\sigma^2)$

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します． 次に，[ファイル]-[保存]をクリックして，スクリプトを保存します． このとき，ファイル名はchapter8としてください． また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

母数の推定

母集団の特徴を表す基本統計量は母数と呼ばれます． 平均，分散などがその代表であり，母集団の平均を母平均$\hat{\mu}$， 母集団の分散を母分散 $\hat{\sigma}^2$と呼びます． また，母集団から抽出された標本の平均を標本平均 $\mu$， 標本の分散（不偏分散）を標本分散 $\sigma^2$と呼びます． テキストによっては，これらの定義が異なることもあるので注意してください．

それでは，母集団から抽出した標本を用いて，母数の値を推定してみましょう． このとき，推定する母数が「1つの値」となっている場合は，点推定 と呼びます． ここでは，平均$\hat{\mu}=100$， 分散$\hat{\sigma}^2=100$に従う母集団を考えます （標準偏差は$\hat{\sigma}=10$）．

$X \sim N(100,100)$

上記の正規分布に従った下記の10000の乱数を生成し，母集団$X$とします． ファイル をダウンロードしたら，read.csv関数を利用して， 変数Xにデータフレームとして読み込んでおきましょう（作業ディレクトリはデスクトップに変更）．

89.74776
96.49404
98.46421
98.99935
93.35153
105.0311
123.9603
98.72574
105.1024
83.61765
...

ファイルを読み込んだら，母集団$X$の平均と分散を求めてみましょう．

X <- read.csv("N-100-10.csv")
> mean(X[,1])
[1] 100.1837
> var(X[,1])
[1] 99.70016

この結果から，母平均$\hat{\mu}=100.18 \simeq 100$， 母分散$\hat{\sigma}^2=99.7 \simeq 100$に従うことが確認できます （標準偏差は$\hat{\sigma}=\sqrt{100} \simeq 10$）． 次に，母集団$X$の確率密度のヒストグラムを描き，分布の形状を確認します．

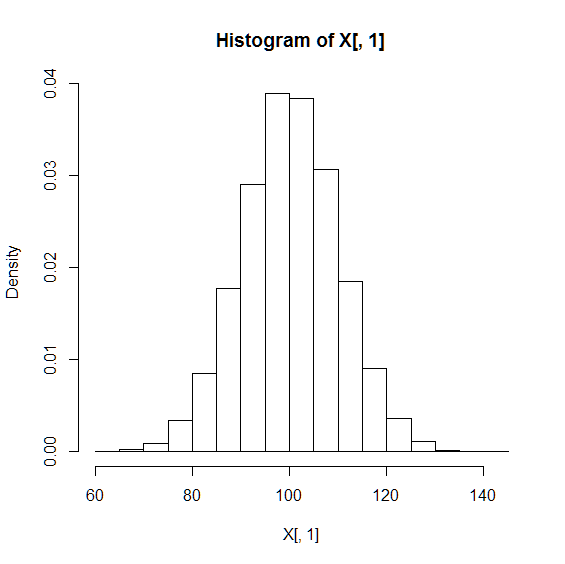
> hist(X[,1],freq=FALSE)

ヒストグラムは釣鐘状になっており，母集団$X$が正規分布に従っていることも確認できました．

それでは，母集団から標本$ｘ$を抽出します． ここで重要なことは，標本は母集団から ランダムサンプリング（無作為抽出） しなくてはならないということです． 無作為に抽出しなければ，標本に偏りが生じる可能性があり，正確な推定ができないことに注意してください． 標本を抽出するにはsample関数を利用します． 引数には抽出するサンプル数$n$として100を指定します．

x <- sample(X[,1],100)

続けて，標本$ｘ$の平均と分散を調べてみましょう．

> mean(x)
[1] 100.4211
> var(x)
[1] 99.90735

この結果から，標本平均$\mu=100.42 \simeq = 100$， 標本分散$\sigma^2=99.91 \simeq = 100$ということが分かりました （標準偏差$\sigma=\sqrt{99.91}=9.99 \simeq 10$）． この値は母平均，母分散とほぼ一致していますね． ただし，抽出する標本が変われば結果も変わることに注意してください．

次に標本$ｘ$の確率密度のヒストグラムを描き，分布の形状を確認します．

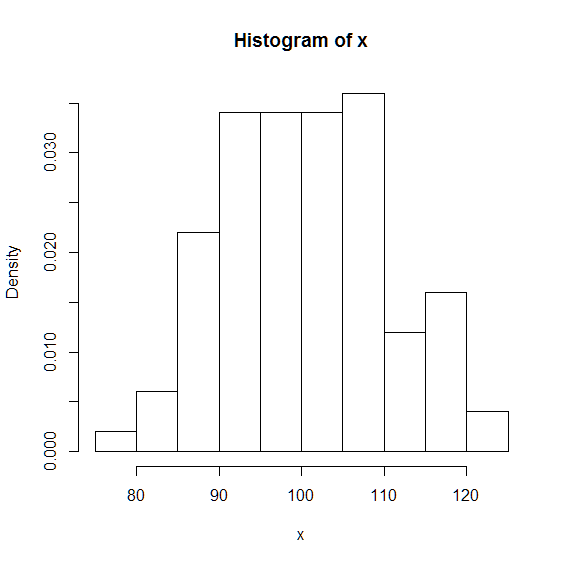
> hist(x,freq=FALSE)

あまり綺麗とはいえませんが，おおまかには釣鐘状の分布をしていることがわかります． どうやら標本$ｘ$も， 平均$\hat{\mu}=100$， 分散$\hat{\sigma}^2=100$に従う正規分布のようです．

$x \sim N(\hat{\mu},\hat{\sigma}^2) = N(100,100)$

上記の結果から分かることを下記にまとめます．

• 母集団$X$が正規分布であれば，ランダムサンプリングした標本$ｘ$も正規分布
• 母平均$\hat{\mu}$は標本平均$\mu$で推定できる
• 母分散$\hat{\sigma}^2$は標本分散（不偏分散）$\sigma^2$で推定できる

標本平均の分布

これまでは母集団$X$と標本$x$の関係を考えました． 次に，母集団$X$と標本平均の分布$m$の関係を考えましょう． この標本平均の分布は，次回のテーマである検定に密接に関係する重要な概念です． 少し回りくどいですが，混乱を避けるためにも，敢えて標本平均の分布という表現を採用します．

それでは，母集団から標本$x$を1000回繰り返して抽出し，その平均を求めます． sample関数を利用し，抽出するサンプル数$n$は10を指定します． 繰り返しにはfor文を利用しますが詳細は割愛します．

m <- double(length=1000)
for(i in 1:1000){
	m[i] <- mean(sample(X[,1],10))
}

続けて，標本平均の分布$m$の平均と分散を調べてみましょう．

> mean(m)
[1] 100.2321
> var(m)
[1] 9.451763

この結果から，標本平均の分布 の平均$\mu=100.23 \simeq 100$， 標本平均の分布 の分散$\sigma^2=9.45 \simeq 10$ということが分かりました （標準偏差$\sigma=\sqrt{9.45}=3.07 \simeq 3.16$）． どうやら平均は母平均とほぼ一致しますが，分散は母分散よりも小さくなるようです．

次に，標本平均の分布$m$の確率密度のヒストグラムを描き，分布の形状を確認します．

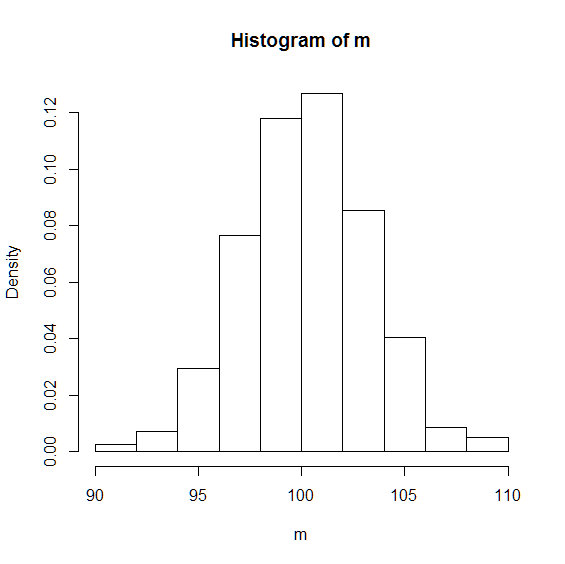
> hist(m,freq=FALSE)

釣鐘上の分布をしており，標本平均の分布$m$も正規分布のようです． 実は，標本平均の分布$m$は， 平均$\mu=\hat{\mu}=100$， 分散$\sigma^2=\frac{\hat{\sigma}^2}{n}=10$に従う正規分布になります． ここで，$n$はサンプル数を意味していることに注意してください．

$m \sim N(\hat{\mu},\frac{\hat{\sigma}^2}{n}) = N(100,10)$

上記の結果から分かることを下記にまとめます．

• 母集団$X$が正規分布であれば，標本平均の分布$m$も正規分布
• 母平均$\hat{\mu}$は標本平均の分布の平均$\mu$で推定できる
• 母分散$\hat{\sigma}^2$は標本平均の分布の分散（不偏分散）$\sigma^2 \times n$で推定できる

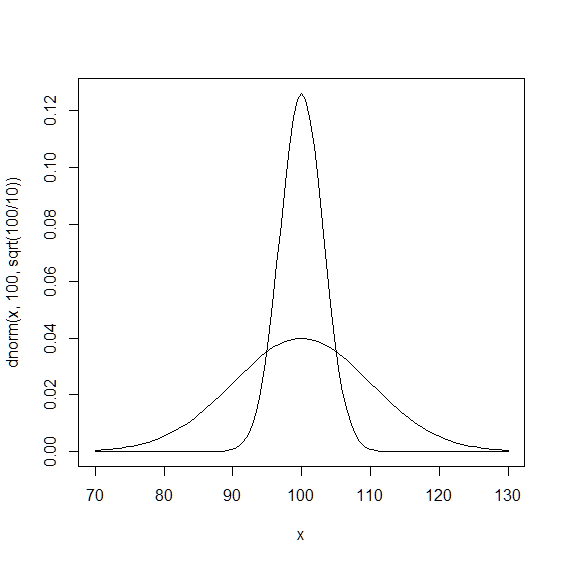
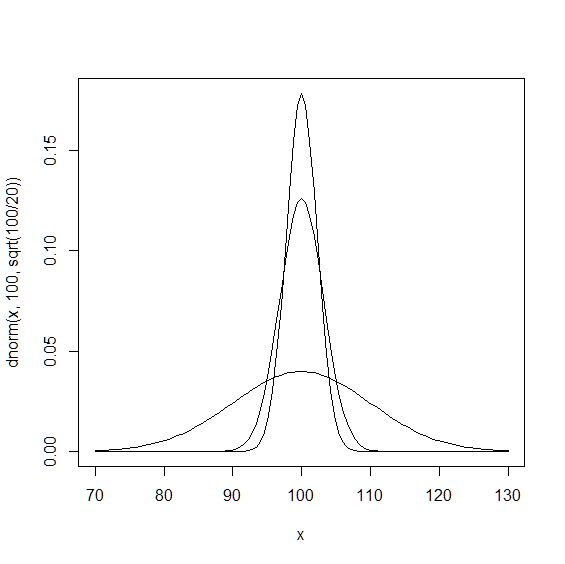
最後に母集団$X$と標本平均の分布$m$の正規分布を描いてみましょう． 平均は一致しますが，分散は 標本平均の分布 の方が小さいため，尖った分布になっていることが分かります．

> curve(dnorm(x,100,sqrt(100/10)),from=70,to=130)
> curve(dnorm(x,100,sqrt(100)),from=70,to=130,add=TRUE)

課題

上記の母集団$X$から， サンプル数$n=20$の標本を抽出したときの， 標本平均の分布を描きなさい． ソースはchapter8.Rに記述し，グラフの画像ファイル，chapter8.R を提出すること．