脳波データをフーリエ解析

フーリエ変換とは

前回までにCortexを利用してEmotiv Epoc+で計測したデータをPythonから取得する方法を説明しました． 一般に，脳波の生データから情報を読み取ることは困難であり，周波数成分に変換することが必要になります． この周波数成分の変換に必要な技術が鬼門のフーリエ変換（Fourier Transform: FT） です． 大学の工学部ではカリキュラムの１つとなっているフーリエ変換（フーリエ級数）に躓いた人も多いのではないでしょうか（何を隠そう向もその一人です）． ここでは，あまり深く考えず，フーリエ変換は 時間領域 から 周波数領域 に変換する仕組みだと理解しておけば十分です．

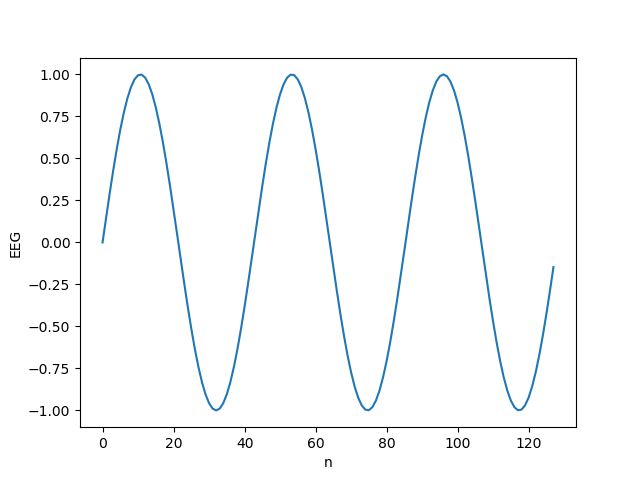
例を挙げて考えてみましょう． Emotivのサンプリングレートは 128Hz であることから，1秒間に 128個の信号が計測されることに注意してください． 仮に計測された脳波が，下記のグラフのような信号だったとします． この信号には，1秒間に 3周期分 のSin関数が含まれています． グラフの横軸が 時間 であることから，このデータは 時間領域 に存在しています．

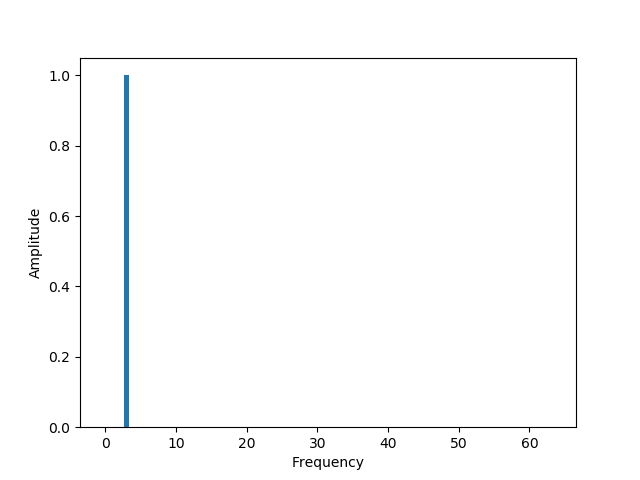
これを，フーリエ変換（高速フーリエ変換）すると下記のグラフになります． このグラフの横軸は 周波数 であり，このデータは 周波数領域 に存在しています． 周波数 が 3 のところに，縦棒がありますよね． この結果は，先のグラフには 周期3 の信号が含まれていることを表しています．

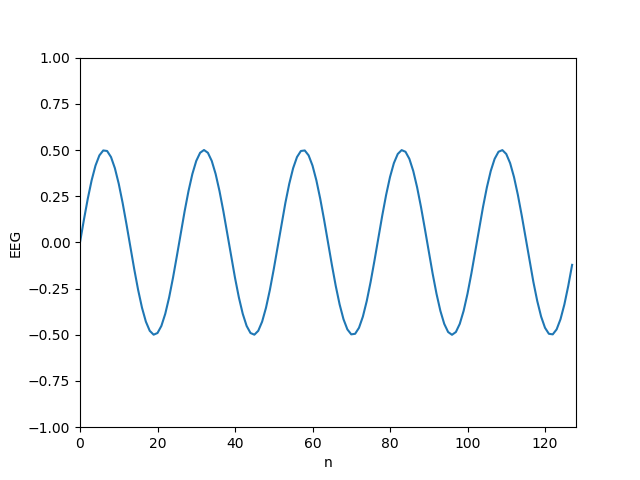
フーリエ変換の凄いところは，異なる周期の信号が混ざっていても，それぞれの周波数成分の強さが取得できることです． 次に，下記のグラフの信号を考えます この信号には，1秒間に 5周期分 のSin関数が含まれています． また，その振幅は先の信号と比べて 1/2 の大きさです．

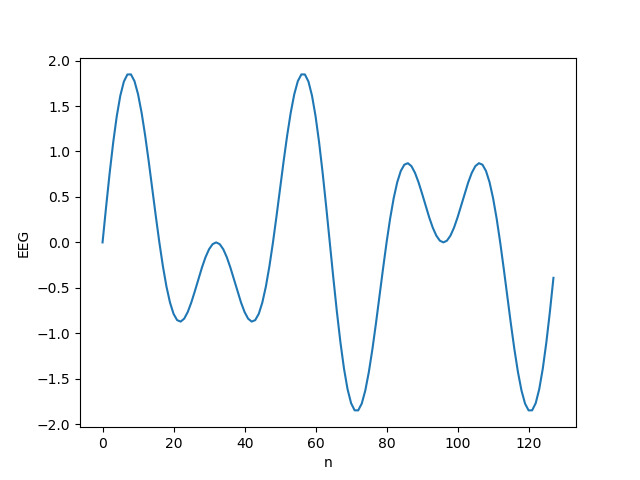
この信号を，先の周期3の信号に加えます（本当に足し算するだけ）． すると，下図のようなグラフになります． これだけで，複雑なグラフになり，人間には理解できないレベルに到達します．

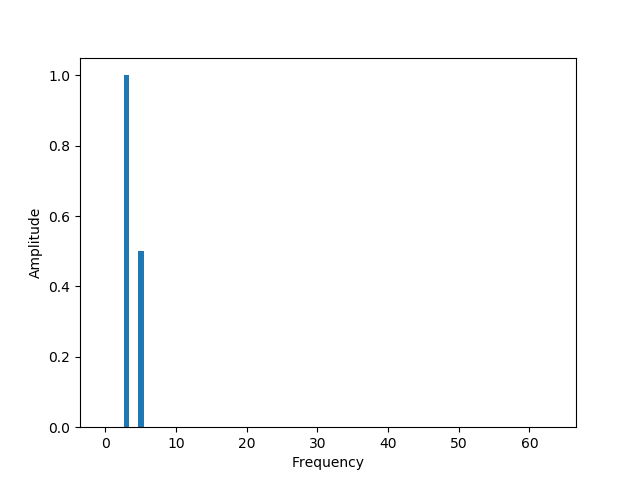
さぁ，フーリエ変換の出番です． 上の周期3と周期5のグラフを加えた信号を変換すると，下記のグラフになります． 周期3 の振幅は 1，また，周期5 の振幅が 0.5 となっていることが読み取れますね． フーリエ級数を発明したジョゼフ・フーリエは本当に天才だと思います（真面目）．

脳波データの記録

それでは，前回までに実装したプログラムを利用して脳波データを取得しましょう． 準備として，数値計算ライブラリのNumpyと，描画ライブラリのmatplotlib.pyplotを導入しておきます．

pip install numpy
pip install matplotlib

Cortexからデータを取得するためのコードは下記です． ここでは，サンプリングレートが128Hz，サンプリング時間は1秒とするため，取得されるデータ数は128になります． 取得されたデータはsignalsというリストに追加されます． また，コード中のEEGDataは独自に実装したクラスであり，14箇所の電極の脳波データを保持するために用いています．

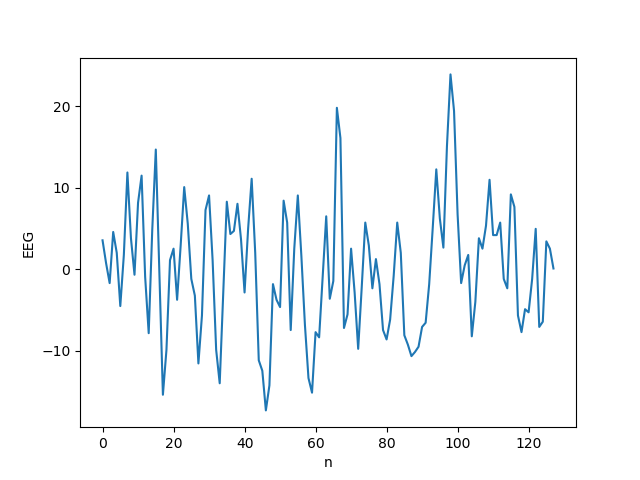
上記で取得したデータをグラフで可視化してみましょう． 可視化するためのコードは下記です． ここでは，後頭部の電極P8に注目しています． 平均値を減算することで正規化していることに注意してください． 自分の脳波を見られて恥ずかしい・・・とは特に思わないですね（笑）

フーリエ変換

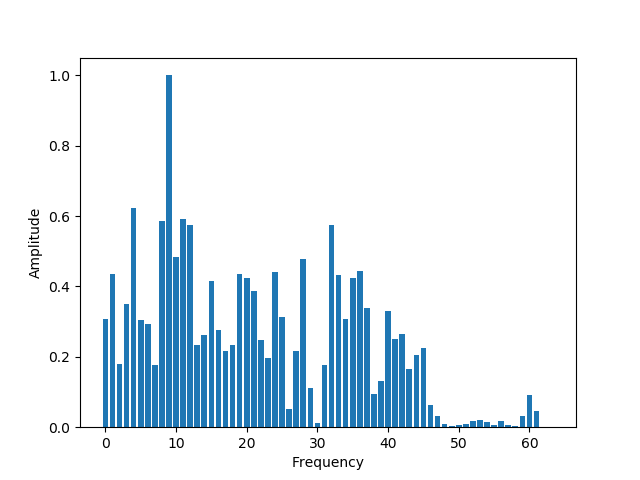
最後に，フーリエ変換を適用します． 準備として，数値解析ライブラリのSciPyを導入しておきます．

pip install scipy

上記で取得した脳波の生データに直接フーリエ変換しても構わないのですが， より特徴的な周波数成分を抽出するには 窓関数 を事前に適用することが一般的です （窓関数の詳細はロジカルアーツ研究所の窓関数を用いる理由を参照してください）． ここでは，周波数分解に向いているとされる ハミング窓 を用います． このハミング窓を取得した脳波の生データに掛ければOKです． SciPyライブラリを用いればフーリエ変換は至極簡単です． フーリエ変換の結果は複素数となるため，絶対値に変換しています． また，振幅も最大値で割ることで，0から1の範囲に正規化しています． グラフを確認すると，どうやら10Hz付近の振幅が大きいようですね． リラックスした状態で発生するアルファ波が有意であると言えそうです．