オープンデータを利用した天候データの相関分析
相関分析とは
相関分析とは,2つの変数XとYの関係性を分析する方法です. 例えば,暑い日にはアイスクリームの売上数が増加すると考えられます. このとき,「X:気温」と「Y:アイスクリームの売上数」には関係がありそうです. 一般に,相関分析には相関係数と呼ばれる評価指標が用いられます(正確にはピアソンの積率相関係数と呼ばれる). 相関係数は-1から1の範囲で与えられ,1に近いほど正の相関,-1に近いほど負の相関を示します.
相関係数は次の式で定義されます. 上記の例で考えると$x_i=\{x_1, x_2, \cdots, x_n\}$は気温を表し, $y_i=\{y_1, y_2, \cdots, y_n\}$はアイスクリームの売上を表します. また,相関係数の式は,xとyの共分散 $\sigma_{xy}$, xの標準偏差 $\sigma_x$, yの標準偏差 $\sigma_y$を用いて表すことも可能です.
$$ 相関係数=\frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \cdot \sqrt{\sum (y_i - \bar{y})^2}} = \frac{\sigma_{xy}}{\sigma_x \cdot \sigma_y} $$
| 相関係数 | 相関の強さ |
|---|---|
| 0.7~1.0 | 強い正の相関 |
| 0.4~0.7 | 正の相関 |
| 0.2~0.4 | 弱い正の相関 |
| -0.2~0.2 | 相関なし |
| -0.4~-0.2 | 弱い負の相関 |
| -0.7~-0.4 | 負の相関 |
| -1.0~-0.7 | 強い負の相関 |
正の相関は,Xが増加するとYも増加する関係を表し,負の相関は,Xが増加するとYが減少する関係性を表します. 先の「気温」と「アイスクリームの売上数」の例では,気温が増加すると,売上数も増加するので正の相関となります. 相関係数はアンケートの分析などでも用いられるメジャーな分析手法の一つです. ここでは,日進市の気温と降水量のオープンデータを対象に相関分析を適用してみましょう.
オープンデータを相関分析
それでは,Google Colaboratoryを利用して,オープンデータの相関分析に挑戦しましょう.
ノートブックの作成
まずは,ノートブックを作成します. ノートブックの名前は chapter2.ipynb に設定します.
前回と同様に相関分析に利用するライブラリを導入します.
matplotlib,pandas,そして,新たに数値計算ライブラリのNumPyをインポートします.
numpyの別名としてnpを指定しています.
!pip install japanize-matplotlib
import matplotlib.pyplot as plt
import japanize_matplotlib
import pandas as pd
import numpy as np
データフレーム(pandas)
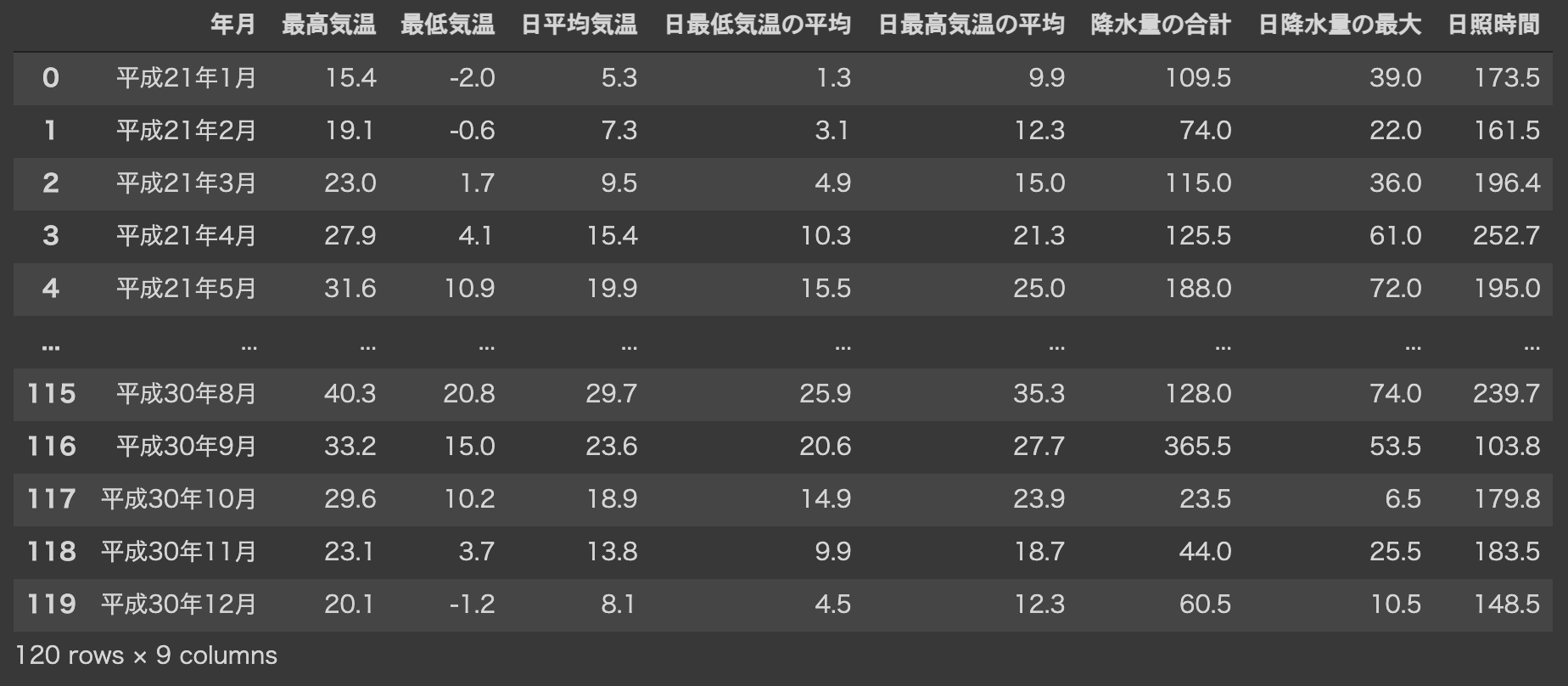
pandasを利用して, CSV形式のオープンデータ(kion.csv)を読み込みます. 平成21年1月から平成30年12月までの日進市の気温や降水量に関するデータです.
# kion.csv
url = "https://mukai-lab.info/classes/seminar_fundamental_areas/csv/kion.csv"
# データフレームの生成(3桁区切りを指定)
df = pd.read_csv(url)
# HTMLで表示(=display(df))
df
日平均気温と降水量の合計
最初に「X:日平均気温」と「Y:降水量の合計」の関係を探ります. 気温の高い夏には雨が多く,気温の低い冬には雨が少ないことが予想されます.
散布図
散布図を作成するにはdf.plot.scatter()を用います.
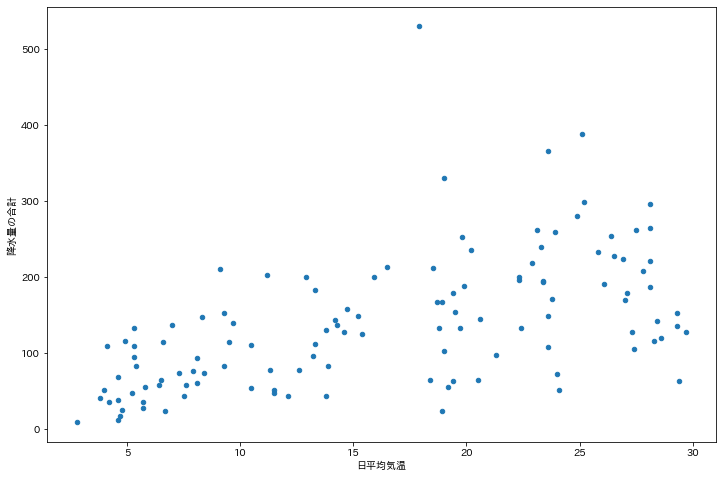
X軸に 日平均気温 ,Y軸に 降水量の合計 をプロットします.
この結果,全体的に右上がりの傾向があることが読み取れます.
df.plot.scatter(x="日平均気温", y="降水量の合計", figsize=(12, 8))
近似直線
この傾向を明確化するために散布図の近似直線を描画します.
近似直線は $y = ax + b$ の式で表され,適切な傾きaと切片bを求める必要があります.
ここでは,np.polyfit()を用いて,近似直線の傾きaと切片bを求めます(2乗誤差の最小化).
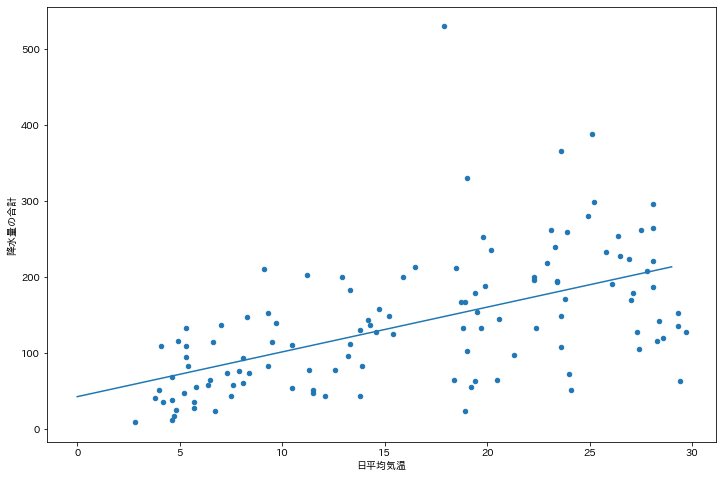
導出の結果,$a \simeq 5.89$,$b \simeq 42.64$という結果になりました.
$a > 0$であることから,日平均気温 と 降水量の合計 には,正の相関があることが読み取れます.
# 近似直線の傾きaと切片b(第3引数の1はxの次数)
a, b = np.polyfit(df["日平均気温"], df["降水量の合計"], 1)
print(f"a={a} b={b}")
# 近似直線のxとy
x = np.arange(0, 30)
y = a * x + b
fig = df.plot.scatter(x="日平均気温", y="降水量の合計", figsize=(12, 8))
fig.plot(x, y)
a=5.894288323846492 b=42.6426477663791
相関係数
相関係数はcorr()で算出することができます.
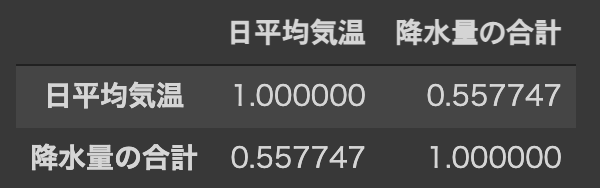
この結果,日平均気温 と 降水量の合計 の相関係数は約$0.56$となりました.
これは 日平均気温 と 降水量の合計 に「正の相関がある」ことを示しています.
df[["日平均気温", "降水量の合計"]].corr()
上記の値が,共分散 $\sigma_{xy}$ と標準偏差$\sigma_x$,$\sigma_y$で算出されることを確認しましょう.
データフレームから,日平均気温と降水量の合計を,tolist()を利用してリストとして取得します.
# x:日平均気温 y:降水量の合計
x = df["日平均気温"].tolist()
y = df["降水量の合計"].tolist()
np.cov()を利用して,xとyの共分散行列($2\times2$の行列)を取得します.
ここで必要なのは,日平均気温と降水量の合計の共分散であるため,行列の[0][1]を取得し,変数covに代入しています.
# 共分散行列からxとyの共分散を取得
cov = np.cov(x, y)[0][1]
print(cov) # -> 404.92605042016794
上記で求めた共分散covと,np.std()で算出したxとyの標準偏差を用いて,相関係数を算出します.
ここで,ddof=1は,不偏標準偏差を算出するためのオプションです.
相関係数は0.557747となり,完全に一致していることが確認できます.
# 相関係数を算出
cor = cov / (np.std(x, ddof=1) * np.std(y, ddof=1))
print(cor) # -> 0.5577472292139701
日照時間と降水量の合計
次に「X:日照時間」と「Y:降水量の合計」の関係を探ります. 日照時間が多い日には雨が少なく,日照時間が少ない日には雨が少ないことが予想されます.
散布図
df.plot.scatter()で散布図を作成します.
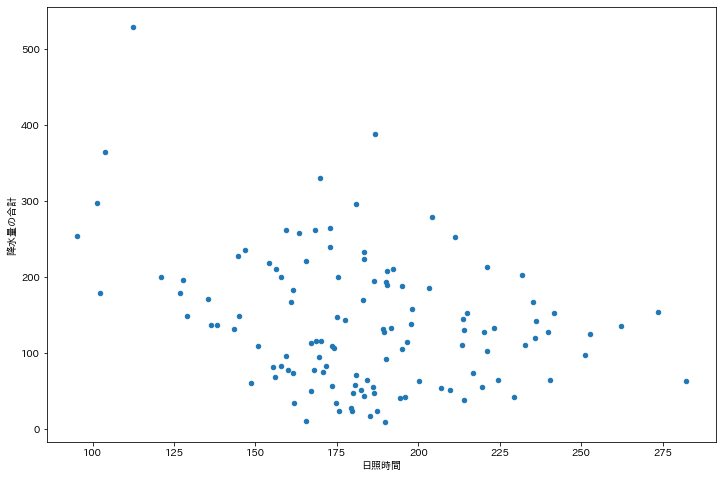
X軸に 日照時間 ,Y軸に 降水量の合計 をプロットします.
この結果,全体的に右下がりの傾向があることが読み取れます.
df.plot.scatter(x="日照時間", y="降水量の合計", figsize=(12, 8))
近似直線
この傾向を明確化するために散布図の近似直線を描画します.
np.polyfit()を用いて,近似直線の傾きaと切片bを求めます.
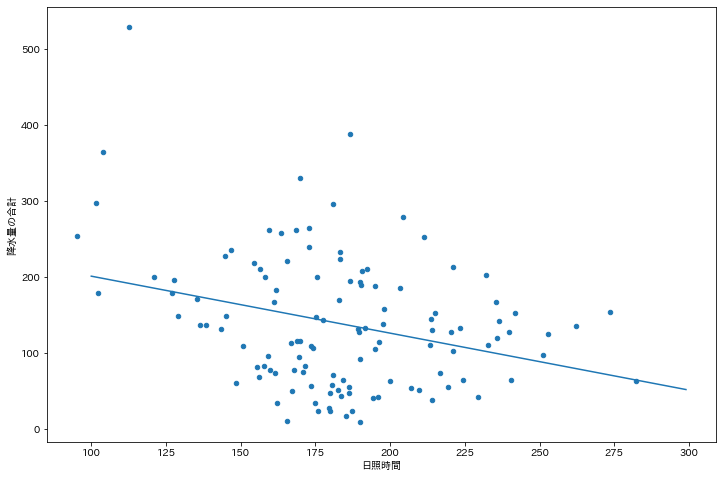
導出の結果,$a \simeq -0.75$,$b \simeq 276.55$という結果になりました.
$a < 0$であることから,日照時間 と 降水量の合計 には,負の相関があることが読み取れます.
# 近似直線の傾きaと切片b
a, b = np.polyfit(df["日照時間"], df["降水量の合計"], 1)
print(f"a={a} b={b}")
# 近似直線のxとy
x = np.arange(100, 300)
y = a * x + b
fig = df.plot.scatter(x="日照時間", y="降水量の合計", figsize=(12, 8))
fig.plot(x, y)
a=-0.7500836696786253 b=276.54845558604035
相関係数
corr()で相関係数を算出します.
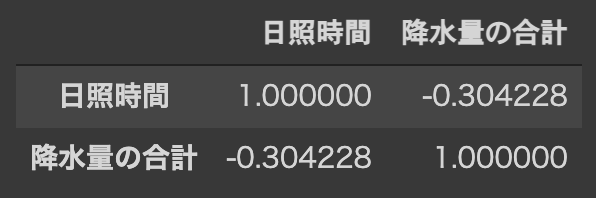
この結果,日照時間 と 降水量の合計 の相関係数は$-0.30$となりました.
これは 日照時間 と 降水量の合計 に「弱い負の相関がある」ことを示しています.
df[["日照時間", "降水量の合計"]].corr()
本日のノートブックは下記URLで確認できます.
課題
Google Colaboratoryで作成した chapter2.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定