Pythonの基礎・フラクタル図形を描いてみよう
フラクタル図形
フラクタル図形 とは,図形の一部が図形の全体と 自己相似 な関係を持つ図形のことです. 特定の処理を再帰的に繰り返して実行することで描くことができます. フラクタル図形は自然界でも観測が可能で,「シダの葉」や「雲の形」はフラクタル図形とされています. ここでは,Pythonの関数の再帰を利用して,コッホ曲線を描くことに挑戦します.
Google Colaboratory
下記のリンクをクリックして,Colabにアクセスしましょう.
Colabにアクセスしたら,大学のGmailアカウント(@g.sugiyama-u.ac.jp)でログインしていることを確認してください. 次に,ノートブック(ファイル)を新規作成し,ノートブックの名前を chapter4.ipynb に変更しましょう.
加えて,前回と同様に,ColabTurtleとインストールしておきます. このとき,多次元配列の処理が可能なライブラリである numpy も追加しておきます.
!pip install ColabTurtle
from ColabTurtle.Turtle import *
import numpy as np
フラクタル図形の描画
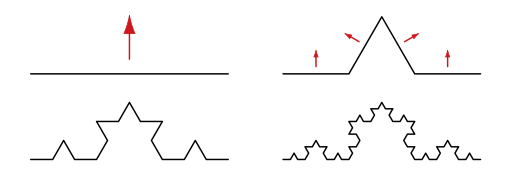
フラクタル図形の一つであるコッホ曲線を描きます. コッホ曲線は与えられた線分を3等分し,分割した2点を頂点とする正三角形を作成する手続きを繰り返すことで得られます.
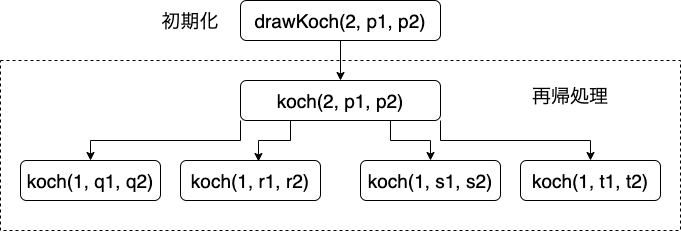
コッホ曲線を描く関数はdrawKochですが,この関数の中でkochを再帰的に呼び出しています(つまりkochの中で,kochを呼び出す).
drawKochの引数は,再帰の次元数(dim),線分の両端の座標(p1とp2)です.
再帰の次元数とは,再帰を繰り返す回数であり,この値が1になるまで繰り返します.
例えば,dim=2で呼び出すと,再帰的にdim=1が4回呼び出さて終了します(4つの直線に分割されるため).
def drawKoch(dim, p1, p2):
points = []
initializeTurtle()
speed(8)
penup()
goto(p1[0], p1[1])
right(90)
koch(dim, p1, p2)
def koch(dim, p1, p2):
p = np.array(p2) - np.array(p1) #線分のベクトル
d = np.linalg.norm(p, ord=2) / 3 #線分を3等分した長さ
q1 = p1 #左の端点
goto(q1[0], q1[1])
if(dim == 1):
pendown()
forward(d)
q2 = position() #1番目の分割点
if(dim > 1):
koch(dim-1, q1, q2) #再起処理
left(60)
forward(d)
q3 = position() #三角形の頂点
if(dim > 1):
koch(dim-1, q2, q3) #再起処理
right(120)
forward(d)
q4 = position() #2番目の分割点
if(dim > 1):
koch(dim-1, q3, q4) #再起処理
left(60)
forward(d)
q5 = position() #右の端点
if(dim > 1):
koch(dim-1, q4, q5) #再起処理
penup()
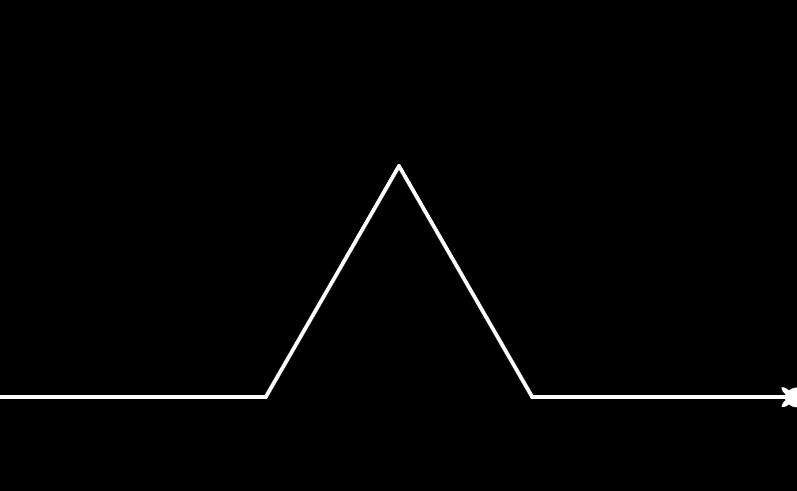
次元数$1$,線分$(0,400)$,$(800,400)$でコッホ曲線を描きます. この結果,次のコッホ曲線が描かれます.
p1 = [0, 400]
p2 = [800, 400]
drawKoch(1, p1, p2)
次元数$2$,線分$(0,400)$,$(800,400)$でコッホ曲線を描きます. この結果,次のコッホ曲線が描かれます.
p1 = [0, 400]
p2 = [800, 400]
drawKoch(2, p1, p2)
次元数$3$,線分$(0,400)$,$(800,400)$でコッホ曲線を描きます. この結果,次のコッホ曲線が描かれます.
p1 = [0, 400]
p2 = [800, 400]
drawKoch(3, p1, p2)
次元数$4$,線分$(0,400)$,$(800,400)$でコッホ曲線を描きます. この結果,次のコッホ曲線が描かれます.
p1 = [0, 400]
p2 = [800, 400]
drawKoch(4, p1, p2)
課題
これまでに学習した方法を活用してオリジナルの図形を描いてください. 描画に際しては次の機能を用いることを必須とします(関数の使用は任意).
- for文による繰り返し
- if文による条件分岐
- 関数の定義と呼び出し
課題が完成したら,Google Colaboratoryで作成した chapter4.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定