Pythonの基礎・関数で図形を描いてみよう
関数
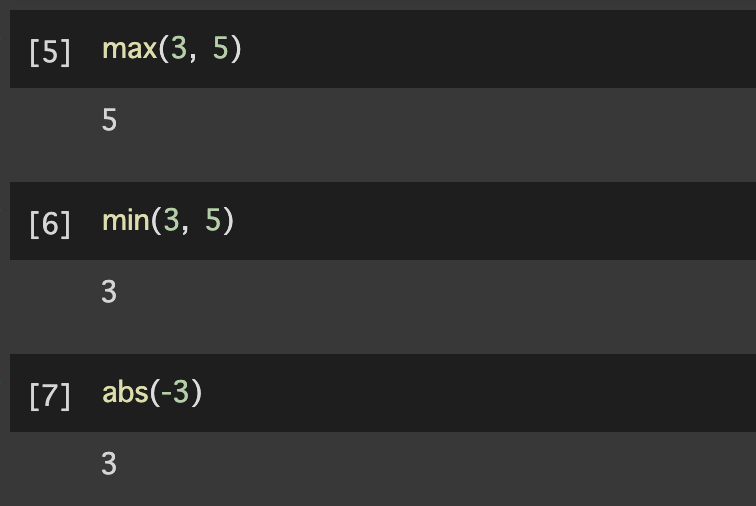
関数 を定義することで,特定の処理に名前を付けて,呼び出すことができます. 関数は,あらかじめ定義されている 組み込み関数 に加え,ユーザ自身が独自に定義することも可能です. 例えば,組み込み関数には下記のような関数があります.
print関数(コンソールに出力する)max関数(最大値を算出する)min関数(最小値を算出する)abs関数(絶対値を算出する)
何度も繰り返して実行する処理は,関数として定義することで,スッキリと記述することができます. ここでは,関数を利用して,効率的に図形を描くことに挑戦しましょう.
Google Colaboratory
下記のリンクをクリックして,Colabにアクセスしましょう.
Colabにアクセスしたら,大学のGmailアカウント(@g.sugiyama-u.ac.jp)でログインしていることを確認してください. 次に,ノートブック(ファイル)を新規作成し,ノートブックの名前を chapter3.ipynb に変更しましょう.
加えて,前回と同様に,ColabTurtleとインストールしておきます. このとき,多次元配列の処理が可能なライブラリである numpy も追加しておきます.
!pip install ColabTurtle
from ColabTurtle.Turtle import *
import numpy as np
関数を利用した図形
関数の定義
関数を定義するには,defの位置から,字下げ して実行する処理を記述します.
ここでは,ランダムにペンの色を変更して,カメを直進させる処理を,forward_random_colorという名前の関数として定義しましょう.
def 関数名():
実行する処理
ペンの色を指定するcolor()は,redやblueなどの色名を指定する他にも,
r(赤),g(緑),b(青)の色成分を指定することができます.
ここでは,np.random.randint(0, 256)を利用して,0〜255までの乱数を生成し,
この乱数をペンの色成分に指定します.
def forward_random_color():
r = np.random.randint(0, 256)
g = np.random.randint(0, 256)
b = np.random.randint(0, 256)
color(r, g, b)
forward(50)
initializeTurtle()
penup()
goto(0, 250)
right(90)
pendown()
for i in range(10):
forward_random_color()
引数
関数を呼び出すときに,引数 という形式で,関数にデータを渡すことができます(引数は複数指定可).
ここでは,カメを直進させるforward()と,カメを右方向に回転させるright()を組み合わせて,
forward_turnという関数を定義しましょう.
def 関数名(引数1,引数2,...):
実行する処理
関数の引数にdistanceとangleを指定しています.
これらの引数には,関数を呼び出したときに設定した値が代入されます.
カメはdistanceだけ直進し,その後で,angleだけ右に回転します.
def straight_turn(distance, angle):
forward(distance)
right(angle)
straignt_turnの引数に100,30,または,200,-30を指定します.
それぞれ,引数のdistanceとangleに代入されます.
initializeTurtle()
penup()
goto(0, 250)
right(90)
pendown()
straight_turn(100, 30)
straight_turn(200, -30)
straight_turn(100, 30)
straight_turn(200, -30)
straight_turn(100, 30)
返り値(戻り値)
関数内で計算した値や文字列を,関数の 返り値(戻り値) として,呼び出し元に返すことができます.
ここでは,0〜99の乱数に応じた距離だけカメを進ませる forward_random() を定義し,
進んだ距離distanceを返り値として,呼び出し元に戻すことにします.
返り値を指定するには return を用います.
def forward_random():
distance = np.random.randint(0, 100)
forward(distance)
return distance
カメが進んだ距離の合計を sum_disntance に記録します.
この値が,300を超えたら,ペンの色を赤色に変更します.
initializeTurtle()
penup()
goto(0, 250)
right(90)
pendown()
sum_distance = 0
for i in range(10):
distance = forward_random()
sum_distance += distance
print(sum_distance)
if sum_distance > 300:
color("red")
多角形の関数
多角形を描く関数drawPolygonを定義してみましょう.
関数には引数として,左上の座標(xとy),頂点数(vertex),辺の長さ(length)を渡すことにします.
頂点数に合わせて,亀が回転するための角度を算出し,辺の数だけ進行方向への移動を繰り返します.
def drawPolygon(x, y, vertex, length):
penup()
goto(x, y)
face(0) # 右を向く
pendown()
sum = 180 * (vertex - 2) # 内角の和
angle = sum / vertex # 内角
for i in range(vertex):
forward(length)
right(180 - angle)
頂点数$4$,辺の長さ$200$で多角形を描きます. この結果,次の正方形が描かれます.
initializeTurtle()
drawPolygon(300, 100, 4, 200)
頂点数$5$,辺の長さ$200$で多角形を描きます. この結果,次の正五角形が描かれます.
initializeTurtle()
drawPolygon(300, 100, 5, 200)
頂点数$6$,辺の長さ$200$で多角形を描きます. この結果,次の正六角形が描かれます.
initializeTurtle()
drawPolygon(300, 100, 6, 200)
頂点数を大きく増やすと,多角形は円に近づきます. ここでは,頂点数$60$,辺の長さ$20$で,円(正確には多角形)を描きましょう.
initializeTurtle()
speed(8)
drawPolygon(300, 100, 60, 20)
課題
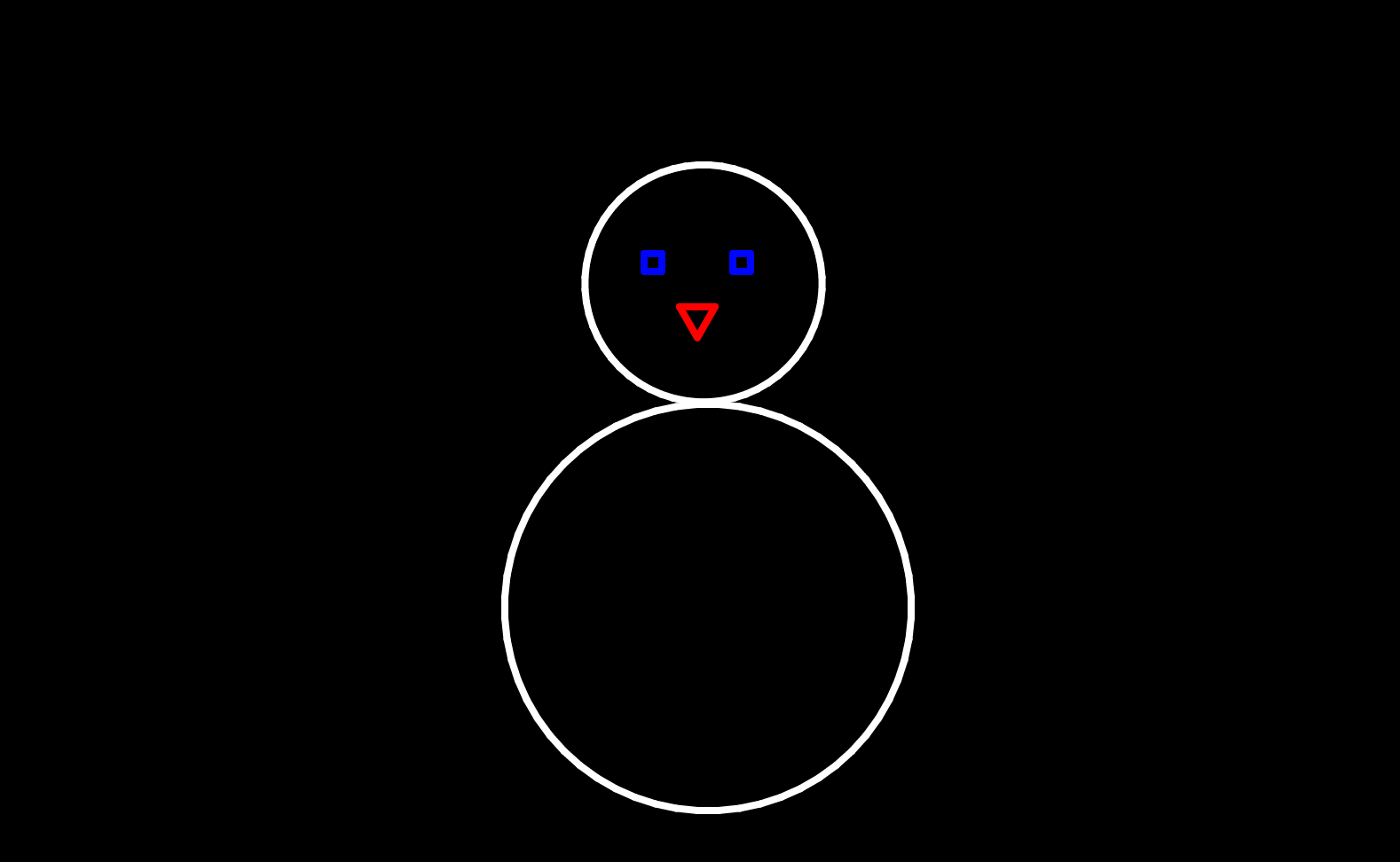
下図を参考に関数を利用して雪だるまを描きなさい.
課題が完成したら,Google Colaboratoryで作成した chapter3.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. 提出の前に必ず下記の設定を行ってください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定