Excelを利用した統計処理・正規分布
授業の準備
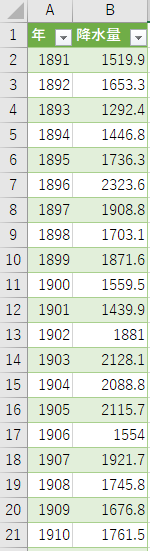
今回、分析対象とするデータは、気象庁が公開している「名古屋の降水量(1891年~2016年)」です。 下記のデータは各年度の降水量(mm)の合計を表しています(1911年以降は省略)。 気象庁では降水量に加え、気圧、気温、湿度など天候に纏わるデータを公開しているので様々なデータを対象に分析すると面白いです。
上記のデータを含むファイルprecipitation.csvをダウンロードしましょう。 ファイルをダウンロードしたら、前回と同様にExcelでprecipitation.csvを読み込んでください。
正規分布
正規分布は、平均値に近い値の頻度が高く、平均値から離れるほど頻度が低くなる特徴を持った確率分布のことです。 前回学んだ2項分布も上記と同じような特徴を持ちますが、2項分布 は離散値(例、コインの表が出る回数)を対象としますが、 正規分布 は連続値(例、降水量)を対象とする点が大きく異なります(実際、2項分布の試行回数nを無限大に近づけると正規分布に一致する)。 一般に、正規分布は様々な自然現象や社会現象に当てはまると考えられており、上記の降水量も例外ではありません。
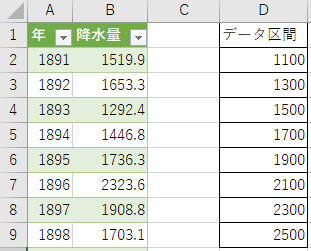
まずは、降水量の分布を確認するために 分析ツール を利用して ヒストグラム(頻度分布) を求めましょう。 最初に、下図のようにD列に1100から2500までのデータ区間(幅は200)を入力します。
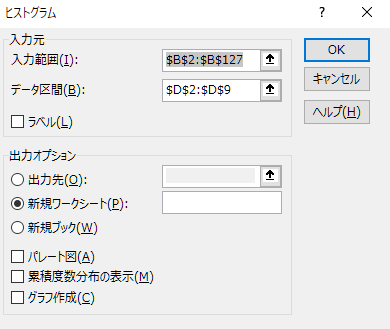
次に、データ タブに切り替え、データ分析 をクリックします。 一覧からヒストグラムを選択し、OKをクリックすると、ダイアログが表示されます。 ダイアログに下記の設定をしてから、ヒストグラムを求めて下さい。
- 入力範囲はB2:B128を設定する
- データ区間はD2:D9を設定する
- 出力オプションで新規ワークシートにチェックを入れる
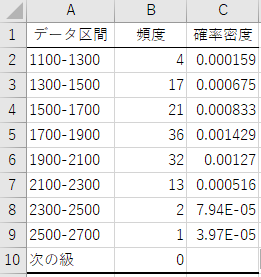
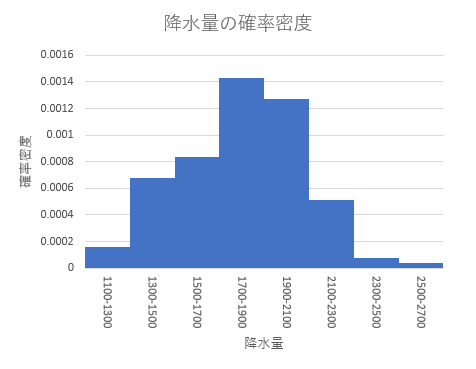
新規に作成されたシートには、1100から2500の範囲で降水量のヒストグラムがまとめられます。 1700-1900が最頻値となっており、この範囲から離れるほど頻度が小さくなることが分かります。 ここで、頻度を基に各データ区間の確率密度を求めましょう(確率 ではないことに注意)。 実際の降水量は連続値ですが、ヒストグラムは離散値であるため、データ区間の幅を考慮しなくてはいけません。 そこで、C列に頻度を、頻度の合計である126と、データ区間の幅200を掛けた25200 で割った値を入力します。 このとき、データ区間も1700-1900のように区間を含めた表現に修正しておきましょう。
さらに、求めた確率密度で棒グラフを描きます。C列をマウスで選択し、挿入 タブの棒グラフをクリックします。 すると、下図のように、横軸が「降水量」、縦軸が「確率密度」である棒グラフが描けます(タイトル、軸ラベル、軸の書式設定を図に合わせて修正してください)。 確率密度を表していることから、棒グラフの面積の総和が1になることが分かります。
このグラフは正規分布に近似することが可能です。 一般にデータサンプルが多いほど、理想的な正規分布の形状に近付きます。
正規分布の公式
正規分布の確率密度は下記の式で与えられます。 2項分布よりも難しく感じると思いますが、この式の重要なパラメータはたった2つです。 1つは平均、もう1つは標準偏差です。 この2つのパラメータで正規分布の形状が決まります。
また、上記の計算はExcelではnorm.dist関数を用いて求めることができます。 それでは、Excelで降水量を近似する正規分布を求めましょう。 まずは、平均、標準偏差を求めます。 平均は1588.5、標準偏差は269.0になります。
- B128に、average関数で平均を求める
- B129に、stdev関数で標準偏差を求める。
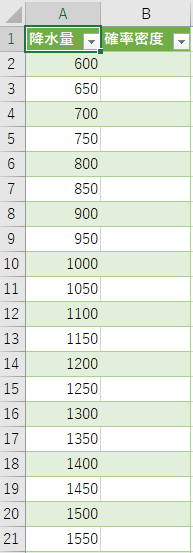
次に、下記データを含むnorm.csvをダウンロードしてください。 ファイルをダウンロードしたらExcelでnorm.csvを読み込んで下さい。
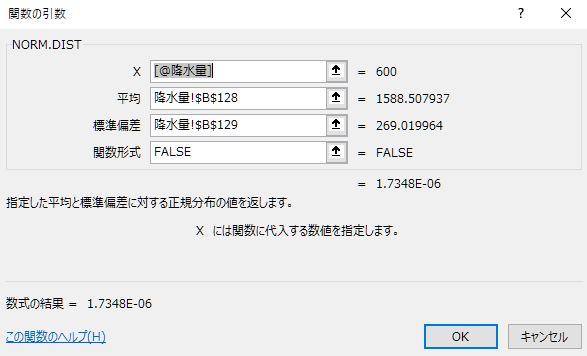
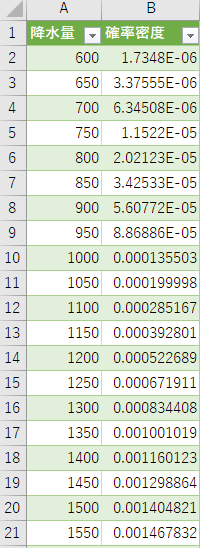
セルB2:B42にnorm.dist関数を用いて確率密度を求めます。 セルB2を選択した状態で、関数の挿入ボタンをクリックし、ダイアログを表示します。 ダイアログでnorm.dist関数を検索し、OKをクリックします。 norm.dist関数の引数には、下図のように3つの引数を指定します(関数形式にtrueを指定すると累積分布になる)。
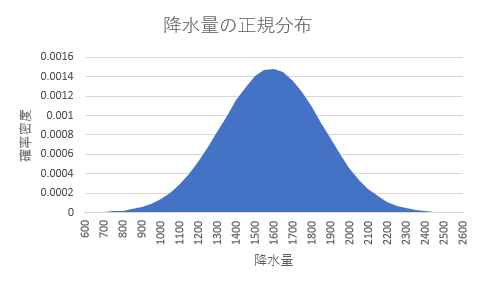
この結果、下記のように連続値を対象とした確率密度が求められます。 上記と同じ手順で面グラフも描きましょう。 このグラフが理想的な正規分布の形状です。 平均の1588が確率密度のピークとなっています。 また、平均を中心に左右対称のグラフとなっていることも分かります。
課題
累積分布を利用することで正規分布の確率を求めることが可能です。 Excelでは、norm.dist関数 の関数形式をtrueにすることで累積分布になります。 降水量の累積分布を利用して下記の設問に答えなさい。
- 降水量が1200[mm]以下になる確率[%]
- 降水量が1800[mm]以上になる確率[%]
- 降水量が1200[mm]~1600[mm]の範囲に含まれる確率[%]