Excelを利用した統計処理・2項分布
授業の準備
今回、分析対象とするデータは、「コインを10回投げる」という試行の結果です。 コイン投げの試行の結果は2通り(表・裏)であり、表を 1 、裏を 0 と表現します。 また、表が出る確率は 50% 、同様に裏が出る確率は 50% と仮定します。 下記のデータは「コインを10回投げる」という試行を100回繰り返したときの結果です(21回目以降の試行は省略)。
上記のデータを含むファイルcoin.csvをダウンロードしましょう。 ファイルをダウンロードしたら、前回と同様にExcelでcoin.csvを読み込んでください。
2項分布
まずは、各試行でコインが表になった回数を数えてみましょう。 表は1で与えられるので、各試行の値の総和が表になった回数を表します。 また、表が出る回数は0から10の範囲に収まります。
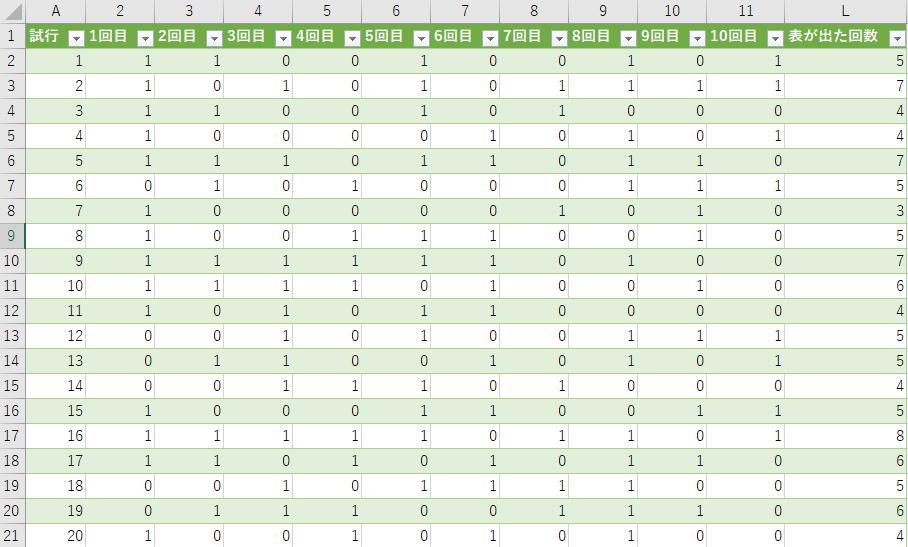
- セルL2:L101に、sum関数で表が出た回数を求める
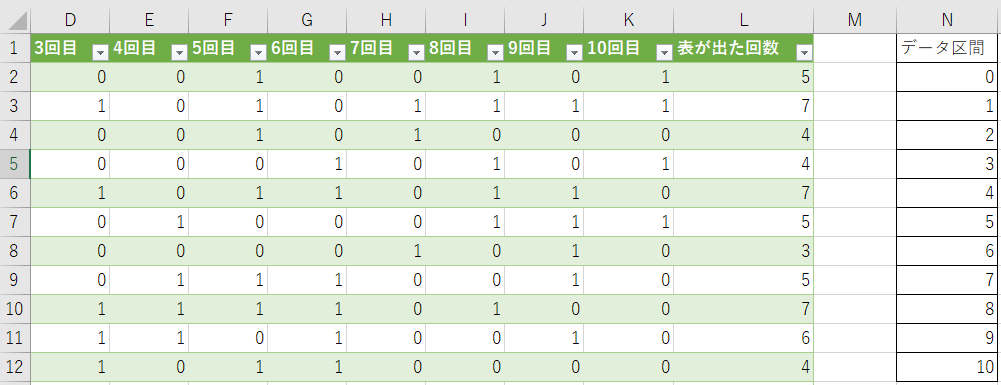
1回目の試行は5回、2回目の試行は7回となりました。 では「コインが表になった回数」はどのような分布になっているか確認するために 分析ツール を利用して ヒストグラム(頻度分布) を求めましょう。 最初に、下図のようにN列に0から10までのデータ区間を入力します。
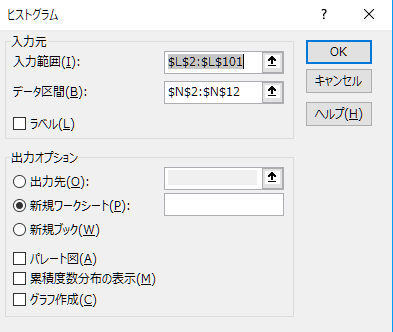
次に、データタブに切り替え、データ分析をクリックします。 一覧からヒストグラムを選択し、OKをクリックすると、ダイアログが表示されます。 ダイアログに下記の設定をしてから、ヒストグラムを求めて下さい。
- 入力範囲にL2:L101を設定する
- データ区間にN2:N12を設定する
- 出力オプションで新規ワークシートにチェックを入れる
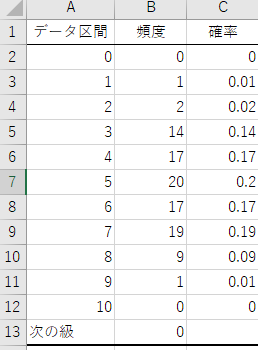
新規に作成されたシートには、0から10の範囲で表が出た回数のヒストグラムがまとめられます。 中央の5回が最頻値となっており、中央から離れるほど頻度が小さくなることが分かります(0回と10回は一度も出現していません)。 ここで、頻度を基に各データ区間の発生確率を求めましょう。 C列に頻度を100で割った値を入力します。
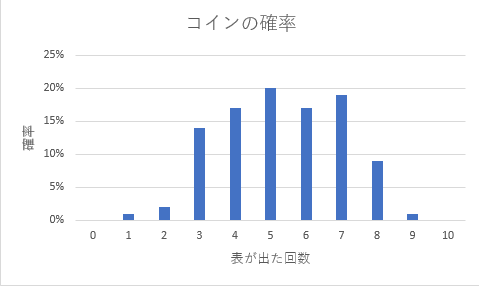
さらに、求めた確率で棒グラフを描きます。 C列をマウスで選択し、挿入タブの棒グラフをクリックします。 すると、下図のように、横軸が「表が出た回数」、縦軸が「確率」である棒グラフが描けます(タイトル、軸ラベル、軸の書式設定を図に合わせて修正してください)。
このグラフは2項分布と呼ばれる確率分布に近似することが可能です。 このデータは100回の繰り返しの結果ですが、試行回数が増えるほどに2項分布の理想の形状に近付きます。
2項分布の公式
では2項分布の理想的な形状を考えましょう。 2項分布は上記のコインのように結果が2通りの試行を対象とします(ベルヌーイ試行 と呼びます)。 また、試行の結果が生じる確率を生起確率と呼びます。 よって、2項分布は「1回の生起確率がpのベルヌーイ試行を、n回行って、k回起こる確率」を表すことになります。
例えば、「コインを5回投げて表が3回出る確率(p=0.5、n=5、k=3)」を考えます。 このとき、「コインを5回投げて表が3回出る組み合わせ」は $ _n C_k = _5 C_3=10$ 通りです。
| 1回目 | 2回目 | 3回目 | 4回目 | 5回目 |
|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 |
また、表が3回出る確率は、 裏が2回出る確率はとなります。 よって、「コインを5回投げて表が3回出る確率」は下記の式で求めることができます。
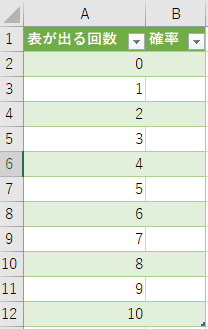
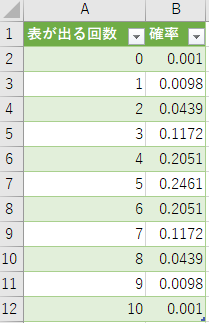
上記の計算はExcelではbinom.dist関数を用いて求めることができます。 それでは、Excelで「コインを10回投げて表がk回出る確率(p=0.5、n=10、k=0~10)」を求めましょう。 まずは、下記データを含むbinom.csvをダウンロードしてください。 ファイルをダウンロードしたらExcelでbinom.csvを読み込んで下さい。
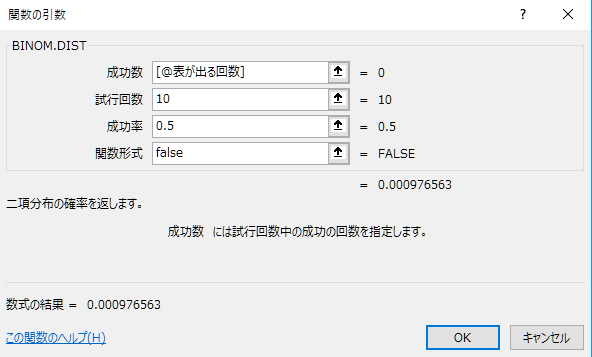
セルB2:B12にbinom.dist関数を用いて確率を求めます。 セルB2を選択した状態で、関数の挿入ボタンをクリックし、ダイアログを表示します。 ダイアログでbinom.dist関数を検索し、OKをクリックします。 binom.dist関数の引数には、下図のように4つの引数を指定します(関数形式にtrueを指定すると累積分布になる)。
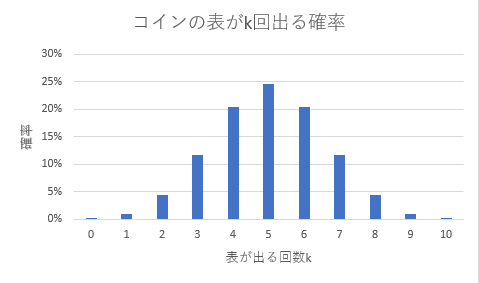
この結果、下記のようにk=0~10の範囲で確率が求められます。 上記と同じ手順で棒グラフも描きましょう。 このグラフが理想的な2項分布の形状です。 中央の5回の確率が最も高く、中央から離れるほど確率は下がります。 また、5回を中心に左右対称となっていることも読み取れます。
課題
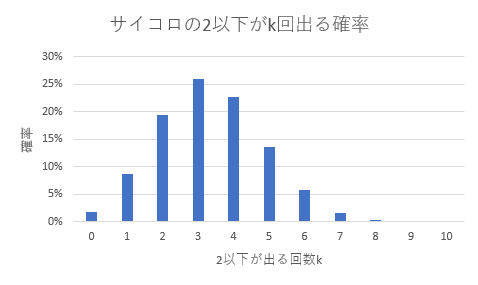
「サイコロを10回投げる」という試行を繰り返したとき、出た目が2以下となる回数の確率分布を求めなさい(サイコロの目は全て均等な確率で出現すると仮定する)。 また、求めた確率分布を利用して下記の設問に答えなさい。
- 2以下の目が6回出る確率
- 2以下の目が3回以下となる確率