Excelを利用した統計処理・相関係数
Microsoft Excelとは
Microsoft Excelはマイクロソフトが開発している表計算ソフトです. 表計算ソフトとは数値データの集計や分析を行うためのソフトウェアのことを指し, Excel以外にもOpenOfficeやGoogleドキュメントなどが存在しますが, Excelが**デファクトスタンダード(事実上の標準)**となっています. 一般に,Excelは,マス目状のセル(入力の単位)で構成されたスプレッドシート(単にシートと呼ぶことが多い)に, 数値,文字列,計算式などのデータを入力することで,財務管理や販売管理などに利用されています. 一方で,Excelには,分析ツール(統計処理) や ソルバー(最適化処理) などの機能が備えられており,統計学的な分析も可能です. この授業では,統計分析の基本である「相関係数」や「2項分布」などを,Excelを用いた実習形式で学ぶことを目的とします. マイクロソフトの認定資格であるマイクロソフト・オフィス・スペシャリスト(MOS)の取得も視野に入れて学習していきましょう.
授業の準備
今回,分析対象とするデータは,20人の5教科(国語,算数,理科,英語,社会)の得点リストです.
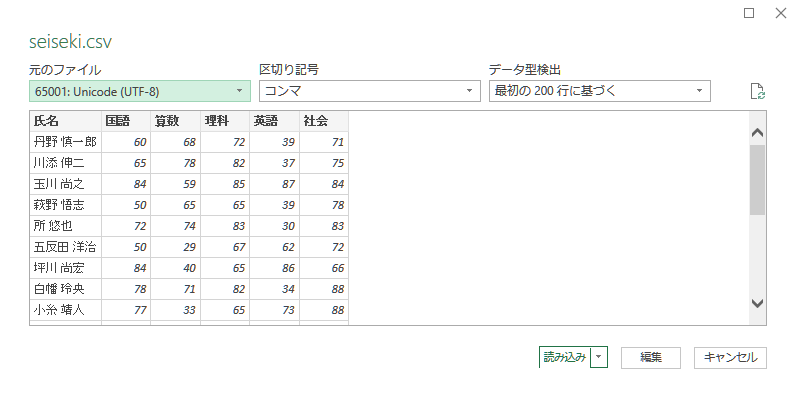
まずは,上記のデータを含むファイル seiseki.csv をダウンロードしましょう. ファイルをダウンロードするには,ファイルのリンクを右クリックをして,「名前を付けてリンク先を保存」を選択します(ブラウザによって異なる). ここで,ファイルは**CSV(Comma Separated Values)**という形式で保存されていることに注意してください. CSV形式では,対象となるデータ(ここでは得点)が,「,(カンマ)」で区切って入力されています(メモ帳で開いて確認してみてください).
ファイルをダウンロードしたら,Excelでseiseki.csvを読み込んでみましょう. Excelを起動し,空白のブック を選択し,ファイルを新規作成します. 次にデータタブに切り替え,テキストまたはCSVから をクリックします. 表示された データの取り込み のダイアログでseiseki.csvを選択し,インポートをクリックします. 最後に,読み込まれるデータを確認したら,読み込みをクリックします.
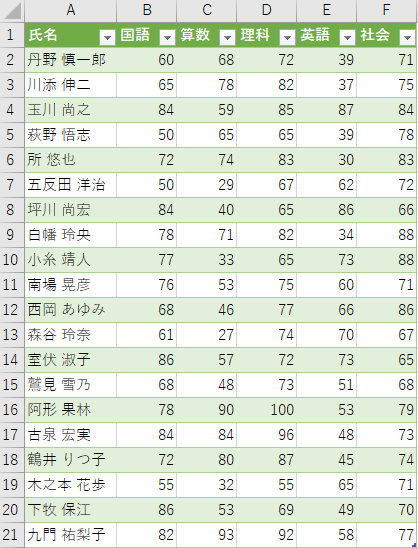
Excelで下記のように表示されていれば成功です. シートの1行目には項目名である氏名,国語,算数,理科,英語,社会が入力されています. また,2行目以降は,20人の生徒の得点リストが入力されています.
相関係数
読み込んだ得点リストのデータを対象に,相関係数 を考えていきましょう. 相関係数とは,2種類のデータの関係の強弱を示す指標です. 例えば,夏の暑い日には,アイスクリームがよく売れますよね. このとき,温度 とアイスクリームの売上 には相関があると言えます. これを定量的に数値で相関の強弱を表したものが 相関係数 です.
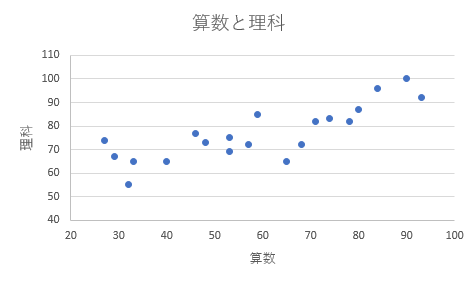
まずは,視覚的に相関係数の意味を捉えていきます. 「算数と理科」の組み合わせで散布図を描きます. 算数のC列と理科のD列をマウスで選択し,挿入タブの散布図をクリックします. すると,下図のように,横軸が算数,縦軸が理科である散布図が描けます(タイトル・軸ラベル・軸の境界値を図に合わせて修正してください).
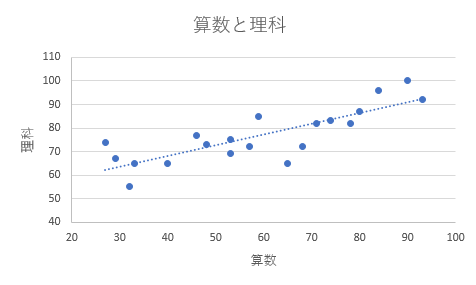
次に,データ系列で右クリックして,近似曲線の追加をクリックしてください. このとき,近似曲線のオプションで線形近似を選択します.
この結果から,算数と理科には右上がりの相関関係があることが分かります. つまり,「算数が得意な生徒は理科も得意」,逆に,「算数が苦手な生徒は理科も苦手」と考えることができます. このような相関関係を正の相関と呼びます.
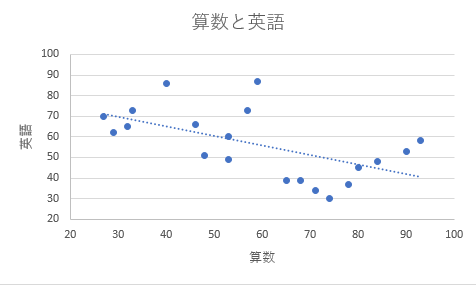
今度は,「算数と英語」の組み合わせて散布図を描きます. 算数のC列と英語のE列をマウスで選択し,挿入タブの散布図をクリックします(離れたセルを選択するにはCtrlキーを押します). すると,下図のように,横軸が算数,縦軸が英語である散布図が描けます(タイトル・軸ラベル・軸の境界値を図に合わせて修正してください). このとき,同様に近似曲線も追加してください.
この結果から,算数と英語には右下がりの相関関係があることが分かります. つまり,「算数が得意な生徒は英語は苦手」,逆に,「算数が苦手な生徒は英語は得意」と考えることができます. このような相関関係を負の相関と呼びます.
相関係数の公式
実際に算数と理科の相関係数を計算してみましょう. 相関係数は下記の式で求めることができます.
$$相関係数 = \frac{算数と理科の共分散}{算数の標準偏差 \times 理科の標準偏差}$$
最初に「偏差の積の平均」を表す共分散を求めます. 偏差とはそれぞれの値と平均値との差を意味します. ここで,算数の得点を$x$,その平均を$\bar{x}$, 同様に,理科の得点を$y$,その平均を$\bar{y}$と表すことにすると, 偏差の積 は下記の式で表されます. これは,下図のように面積を計算していることに等しいことがわかります.
$$(x - \bar{x}) \times (y - \bar{y})$$
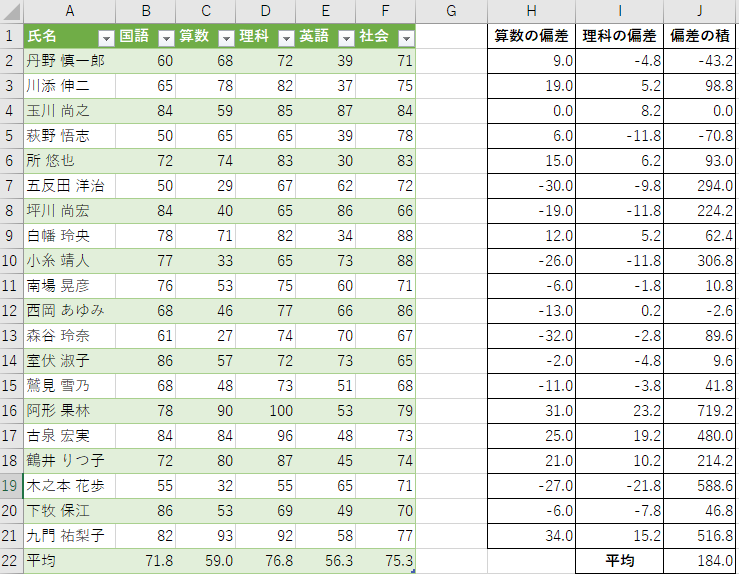
- セルB22:F22に,average関数で5科目の平均値を求める
- セルH2:H21に算数の偏差,セルI2:I21に理科の偏差を求める
- セルJ1:J21に算数と理科の偏差の積を求める
- セルJ22に,average関数で偏差の積の平均(共分散)を求める
この結果,算数と理科の共分散は184.0と分かります. この値を算数と理科の標準偏差の積で割った値が相関係数です.
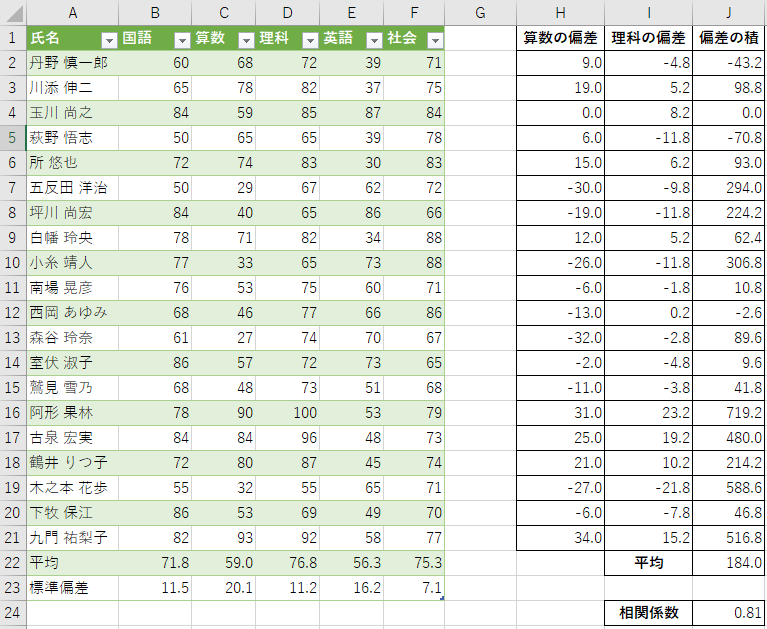
- セルB23:F23に,stdev.p関数 で5科目の標準偏差を求める
- セルJ24に,
=J22/(C23*D23)を入力し,相関係数を求める
最終的に算数と理科の相関係数は0.81になりました. これは強い正の相関を意味しています.
上記で求めたように相関係数は-1から1の範囲をとり, 1に近いほど正の相関となり,-1に近いほど負の相関となります. 一般に相関の強さは下記表で分類します.
| 相関係数 | 相関の強さ |
|---|---|
| 0.7~1 | 強い正の相関 |
| 0.4~0.7 | 正の相関 |
| 0.2~0.4 | 弱い正の相関 |
| -0.2~0.2 | 相関なし |
| -0.4~-0.2 | 弱い負の相関 |
| -0.7~-0.4 | 負の相関 |
| -1~-0.7 | 強い負の相関 |
分析ツールの利用
分析ツールを利用して相関係数を求めましょう. 分析ツールは,Excelのアドインであり,相関係数だけでなくt検定など高度な統計的分析が可能なツールです.
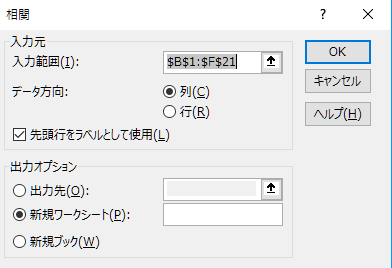
データタブに切り替え,データ分析をクリックします. 一覧から相関を選択し,OKをクリックすると,ダイアログが表示されます. ダイアログに下記の設定をしてから,相関係数を求めて下さい.
- 入力範囲にB1:F21を設定する
- 「先頭行をラベルとして使用」にチェックを入れる
- 出力オプションで新規ワークシートにチェックを入れる
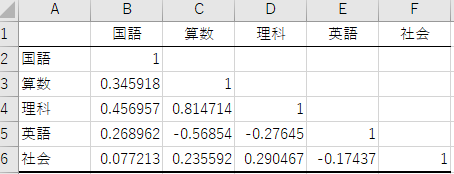
新規に作成されたシートには,下記のように5科目間の相関係数が表形式でまとめられます. 「算数と理科の相関係数」と「算数と英語の相関係数」が先程求めた値と一致していることが分かります. また,同じ科目(例,算数と算数)の相関係数は1であり,1が並ぶ対角線に沿って相関係数は対称となります (つまり「算数と理科の相関係数」と「理科と算数の相関係数」は一致).
課題
完成したエクセルファイルを保存し,Glexaから提出しなさい(ファイル名は任意で構わない).