線形計画法②・最短経路問題
最短経路問題
重み付き有向グラフの2点間を結ぶ最短経路を導出する 最短経路問題 に挑戦しましょう. 最短経路問題も,最適生産計画と同様に,線形計画問題の一つとして扱うことが可能です.
例題
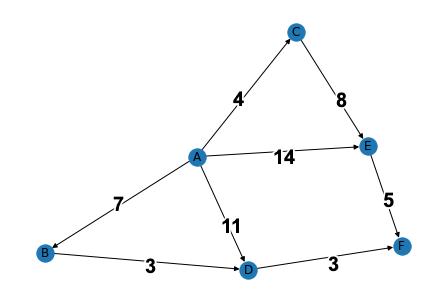
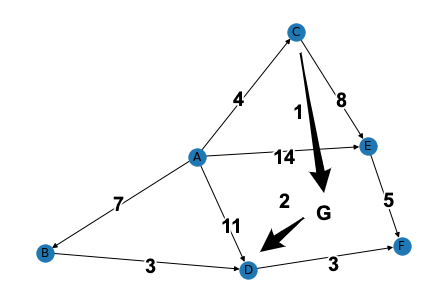
AからFまでの6つの都市(ノード)がある. Aを始点,Fを終点としたとき,2都市間を結ぶ最短の経路を求めよ. このとき,都市間の移動はエッジの向きに限定される. また,都市間の距離(コスト)は,エッジの重みとして与えられる.
まずは,解となり得る経路を列挙してみましょう. 経路の距離を比較してみると,$A \rightarrow B \rightarrow D \rightarrow F$が最短であることが分かります.
$$ A \rightarrow B \rightarrow D \rightarrow F (距離: 13) $$
$$ A \rightarrow C \rightarrow E \rightarrow F (距離: 17) $$
$$ A \rightarrow D \rightarrow F (距離: 14) $$
$$ A \rightarrow E \rightarrow F (距離: 19) $$
問題を定式化するために,変数$x_{ij}$を導入します. ノード$i$からノード$j$の経路を含むときは$x_{ij}=1$,経路を含まないときは$x_{ij}=0$とします. この$x_{ij}$を用いて,目的関数は次のように定義することができます. ここで,$w_{ij}$は,ノード$i$からノード$j$までの距離,$E$はエッジの集合を表します.
$$ 経路長 = \sum_{i,j \in E} w_{ij} \cdot x_{ij} $$
例えば,$A \rightarrow D \rightarrow F$の経路の場合は,$x_{AD}=1,x_{DF}=1$であり,その他は$0$となります. 経路長は,次の式で計算され,その値は14となります($x_{ij}=0$の項は消える).
$$ 経路長 = w_{AD} \cdot x_{AD} + w_{DF} \cdot x_{DF} = 11 \cdot 1 + 3 \cdot 1 = 14 $$
| $x_{AB}$ | $x_{AC}$ | $x_{AD}$ | $x_{AE}$ | $x_{BD}$ | $x_{CE}$ | $x_{DF}$ | $x_{EF}$ |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| $w_{AB}$ | $w_{AC}$ | $w_{AD}$ | $w_{AE}$ | $w_{BD}$ | $w_{CE}$ | $w_{DF}$ | $w_{EF}$ |
|---|---|---|---|---|---|---|---|
| 7 | 4 | 11 | 14 | 3 | 8 | 3 | 5 |
次に制約条件を定義します. 制約条件は,始点の条件,終点の条件,中間地点の条件の3種類に分類されます.
始点の条件を考えます. 経路は必ずAから始まるため,Aから他のノードに遷移するための経路$x_{Aj} = \left\{ x_{AB}, x_{AC}, x_{AD}, x_{AE} \right\}$のいずれかが,必ず最短経路に含まれることになります. よって,次の条件を満たすことになります.
$$ Aの条件: x_{AB} + x_{AC} + x_{AD} + x_{AE} = 1 $$
終点の条件を考えます. 経路は必ずFで終わるため,他のノードからFに遷移するための経路$x_{iF} = \left\{ x_{DF}, x_{EF} \right\}$のいずれかが,必ず最短経路に含まれることになります. よって,次の条件を満たすことになります.
$$ Fの条件: x_{DF} + x_{EF} = 1 $$
中間地点の条件を考えます. ここでは,中間地点であるDを例に考えます. Dを通過する場合は,他のノードからDに遷移するための経路$x_{iD} = \left\{ x_{AD}, x_{BD} \right\}$のいずれかが,必ず最短経路に含まれることになります. 同様に,Dから他のノードに遷移するための経路$x_{Dj} = \left\{ x_{DF} \right\}$も,必ず最短経路に含まれることになります. よって,次の条件を満たすことになります. この条件はDを通過しない場合も成立することに注意してください($x_{AD}=0$,$x_{BD}=0$,$x_{DF}=0$であるため).
$$ Dの条件: (x_{AD} + x_{BD}) - x_{DF} = 0 $$
他の中間地点となるノードにも条件が設定できます.
$$ Bの条件: x_{AB} - x_{BD} = 0 $$
$$ Cの条件: x_{AC} - x_{CE} = 0 $$
$$ Eの条件: (x_{AE} + x_{CE}) - x_{EF} = 0 $$
上記の目的関数と制約条件を利用して,線形計画問題を解くことで,最短経路の算出が可能となります.
データセット
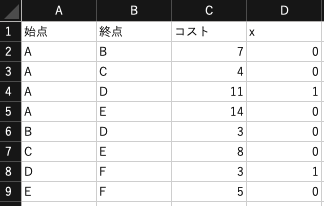
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 上述と同じ最短経路問題であり,エッジに付与された距離(コスト)を表しています.
始点,終点,コスト
A,B,7
A,C,4
A,D,11
A,E,14
B,D,3
C,E,8
D,F,3
E,F,5
Excelで最短経路問題
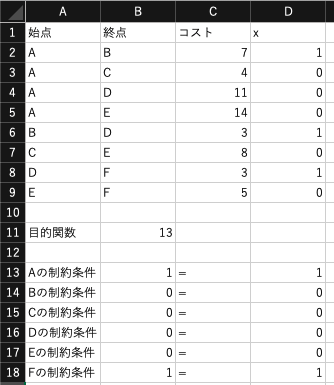
Excelのソルバーを利用して最短経路問題を解きましょう. ダウンロードしたファイルをExcelで開いてください.
変数
D列に変数$x_{ij}$を入力します. 初期状態では,$A \rightarrow D \rightarrow F$を表すために,$x_{AD}=1$,$x_{DF}=1$に設定しましょう.
目的関数
B11に目的関数を表す=SUMPRODUCT(C2:C9,D2:D9)を入力します.
SUMPRODUCT関数は,指定された列(行)の要素同士を掛けてから,足し合わせた値を算出します.
ここでは,$w_{AD} \cdot x_{AD} + w_{DF} \cdot x_{DF} = 14$となります.
制約条件
B13:D18に制約条件を入力します.
B13は始点の条件である=D2+D3+D4+D5,B18は終点の条件である=D8+D9を入力します.
その他は中間地点の条件であり,例えばBの制約条件であるB14は,=D2-D6と入力します.
ソルバー
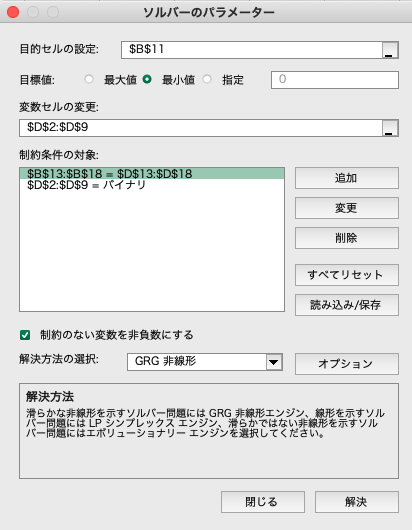
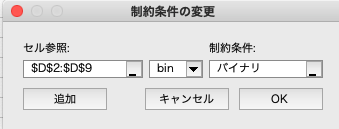
データ・タブからソルバーを選択します. ソルバーのパラメータに,目的セル(目的関数),変数セル(変数),制約条件の対象(制約条件)を設定します. このとき,$x_{ij}$は,0と1の2値であるため, 制約条件としてバイナリ(bin)を設定しておきます. また,解決方法はGRG非線形を選択します(シンプレックス法でも解けるはずだがなぜか不安定).
最後に解決ボタンをクリックすると,最適な$x_{ij}$が導出されます. この結果,$A \rightarrow B \rightarrow D \rightarrow F$が最短経路として導出され, この経路の距離(コスト)が13であることも分かります. また,この解が全ての制約条件を満たしていることも分かります.
Pythonで最短経路問題
Pythonを利用して最適生産計画を解きましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter9.ipynb とします.
pandas,matplotlib,numpy,PuLPなどのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
from pulp import *
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset8.csv")
display(df)
変数
PuLPを利用して変数$x_{ij}$をリストで定義します.
データのカテゴリとしてcat="Binary"を指定します.
# 変数
x_list = []
for i in range(len(df)):
x = LpVariable("x" + str(i), cat="Binary")
x_list.append(x)
問題
最短経路問題を定義します.
ここで,LpMinimizeを指定し,目的関数を最小化することを指定します.
# 問題
problem = LpProblem("最短経路問題", LpMinimize)
目的関数
目的関数を定義します.
lpSum()関数は,LpVariable型の変数の加算を表します.
# 目的関数
problem += lpSum(x_list * df["コスト"])
制約条件
制約条件を定義します.
# 始点の条件
problem += x_list[0] + x_list[1] + x_list[2] + x_list[3] == 1, "Aの条件"
# 終点の条件
problem += x_list[6] + x_list[7] == 1, "Fの条件"
# 中間地点の条件
problem += x_list[0] - x_list[4] == 0, "Bの条件"
problem += x_list[1] - x_list[5] == 0, "Cの条件"
problem += (x_list[2] + x_list[4]) - x_list[6] == 0, "Dの条件"
problem += (x_list[3] + x_list[5]) - x_list[7] == 0, "Eの条件"
問題の確認
定義した問題を確認してみましょう. 目的関数,制約条件,変数の条件などを確認することができます.
print(problem)
最短経路問題:
MINIMIZE
7*x0 + 4*x1 + 11*x2 + 14*x3 + 3*x4 + 8*x5 + 3*x6 + 5*x7 + 0
SUBJECT TO
Aの条件: x0 + x1 + x2 + x3 = 1
Fの条件: x6 + x7 = 1
Bの条件: x0 - x4 = 0
Cの条件: x1 - x5 = 0
Dの条件: x2 + x4 - x6 = 0
Eの条件: x3 + x5 - x7 = 0
VARIABLES
0 <= x0 <= 1 Integer
0 <= x1 <= 1 Integer
0 <= x2 <= 1 Integer
0 <= x3 <= 1 Integer
0 <= x4 <= 1 Integer
0 <= x5 <= 1 Integer
0 <= x6 <= 1 Integer
0 <= x7 <= 1 Integer
解決
solve()関数で問題を解きます.
この関数の戻り値が1(Optimal)のときは,最適解が得られたことを表します.
status = problem.solve()
print(LpStatus[status])
Optimal
導出された最適解を確認しましょう. Excelのソルバーで導出された解と同じ,$A \rightarrow B \rightarrow D \rightarrow F$が最短経路として導出されたことが分かります. また,この経路の距離(コスト)が13であることも確認できます.
# 最適化された変数の確認
for x in x_list:
print(x.varValue)
# 経路コスト
print(problem.objective.value())
1.0
0.0
0.0
0.0
1.0
0.0
1.0
0.0
13.0
課題
新たにノードGを追加し,AからFの最短経路を算出しなさい.
df_temp = pd.DataFrame({
"始点": ["C", "G"],
"終点": ["G", "D"],
"コスト": [1, 2]
})
df2 = pd.concat([df, df_temp]).reset_index(drop=True)
display(df2)
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter9.ipynb としてください.