統計的仮説検定③・ANOVA
3群の平均値差の検定
これまでに学習したt検定は,2群の平均値差の検定には有効ですが,3群以上の平均値差の検定に用いることができません. まずはこの理由から考えてみましょう.
検定の多重性
例えば,3つの小学校の50メートル走のタイムを考えます. このとき,t検定を利用して,3つの小学校のタイムの平均値差を検定することを考えます. 帰無仮説は$\mu_A = \mu_B = \mu_C$であり,有意水準は$\alpha=0.05$(5%)とします.
| A小学校 | B小学校 | C小学校 |
|---|---|---|
| 12.4 | 11.5 | 10.9 |
| 11.8 | 12.3 | 10.6 |
| 10.3 | 13.2 | 11.1 |
| 12.0 | 10.8 | 9.9 |
| 13.2 | 11.3 | 10.2 |
t検定は2群の平均値差の検定のため,次の組み合わせで3回のt検定を適用しなくてはいけません.
- A小学校とB小学校(帰無仮説: $\mu_A = \mu_B$)
- B小学校とC小学校(帰無仮説: $\mu_B = \mu_C$)
- C小学校とA小学校(帰無仮説: $\mu_C = \mu_A$)
この場合,検定の多重性 という問題が生じます. この3つに分けた検定のうち,少なくとも1つが有意差有り($p値 < \alpha$)となる確率は次のように求めることができます(1から「全てが有意差なしの確率」を引く).
$$ 1 - (1 - \alpha)^3 = 1 - 0.95^3 \simeq 0.143 $$
つまり,本来は$\mu_A = \mu_B = \mu_C$という帰無仮説に対して,有意水準5%の検定をしたかったのに,実際は有意水準14.3%の検定になってしまっています. 有意水準が高くなることことから,「有意差有り」という結果に繋がりやすく,インチキな結果と捉えかねられません.
ANOVA(分散分析)
そこで,3群以上の平均値差の検定には ANOVA(Analysis of Variance) という手法が用いられます. 日本語では分散分析と呼ばれますが,平均値の差を検定する手法です.
帰無仮説と対立仮説
ANOVAの帰無仮説と対立仮説は次のように表すことができます. 対立仮説は,3群のうち1つだけ母平均が異なる場合でも成立することに注意が必要です(ANOVAではどの組み合わせの郡で有意差があったかは判断できない).
帰無仮説: 「3群が属する母集団の平均は等しい」
- $\mu_A = \mu_B = \mu_C$
対立仮説: 「3群が属する母集団の平均は等しくない」
- $\mu_A = \mu_B \neq \mu_C$
- $\mu_A \neq \mu_B = \mu_C$
- $\mu_A = \mu_C \neq \mu_B$
- $\mu_A \neq \mu_B \neq \mu_C$
検定統計量
分散分析の検定統計量は F比 が用いられます. F比は 効果の分散 と 誤差の分散 の比を表しています.
$$ F比 = \frac{効果の分散}{誤差の分散} = \frac{群間平方和 / 群間の自由度}{群内平方和 / 群内の自由度} $$
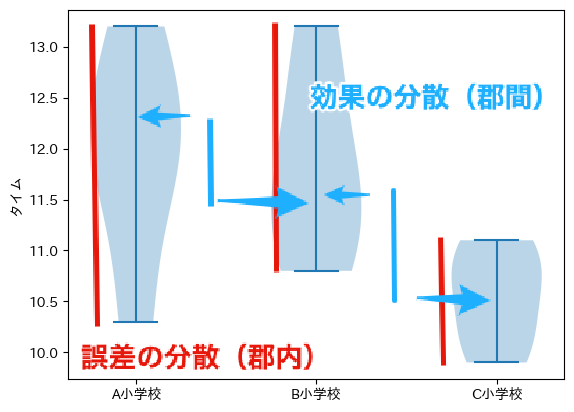
次のグラフは3つの小学校の50メートル走のタイムのバイオリンプロット(確率分布をカーネル密度推定で算出したグラフ)です. 効果の分散は,バイオリン同士の距離の大きさを表し,群間でタイムに差があったことを示す値です. 一方,誤差の分散は,バイオリン自体の大きさを表し,群内におけるタイムの散らばりを示す値です. このため,F比が大きいほど,群間の有意差が大きくなることを示します.
この検定統計量は,3群が属する母集団の平均が等しいとき(帰無仮説が成立するとき),F分布に従うことが知られています. F分布は 群間の自由度 dfn(degree of freedom numerator) と 群内の自由度 dfd(degree of freedom denominator) によって形状が定まります. 群間の自由度は,群(A小学校,B小学校,C小学校)の数から1を引いた値です. また,群内の自由度は,サンプルサイズ($n=15$)から,群の数を引いた値です.
$$ dfn = 3 - 1 = 2 $$
$$ dfd = 15 - 3 = 12 $$
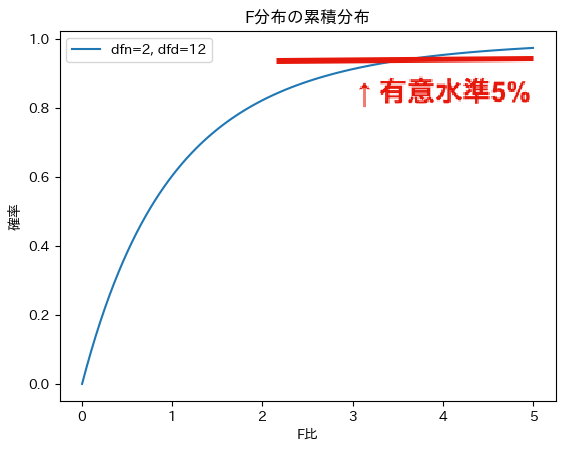
次に群間の自由度 $dfn=2$,群内の自由度$dfd=12$のF分布の累積分布を示します. 有意水準を$\alpha=0.05$(5%)とするとき,棄却域は$F > 3.89$となります.
データセット
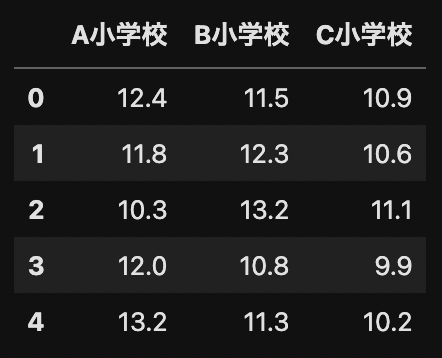
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 3つの小学校の生徒の50メートル走のタイムです.
A小学校, B小学校, C小学校
12.4, 11.5, 10.9
11.8, 12.3, 10.6
10.3, 13.2, 11.1
12, 10.8, 9.9
13.2, 11.3, 10.2
ExcelでANOVA
Excelの分析ツールを利用してANOVAを試してみましょう. ダウンロードしたファイルをExcelで開いてください.
分析ツール
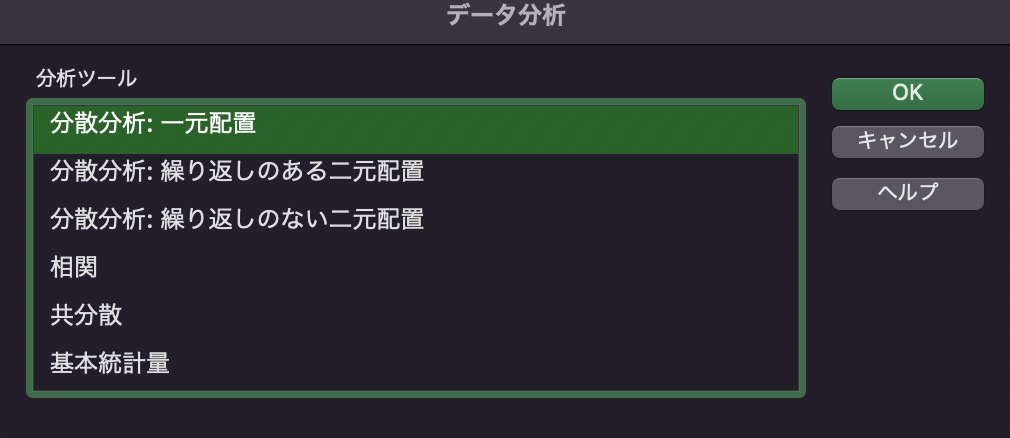
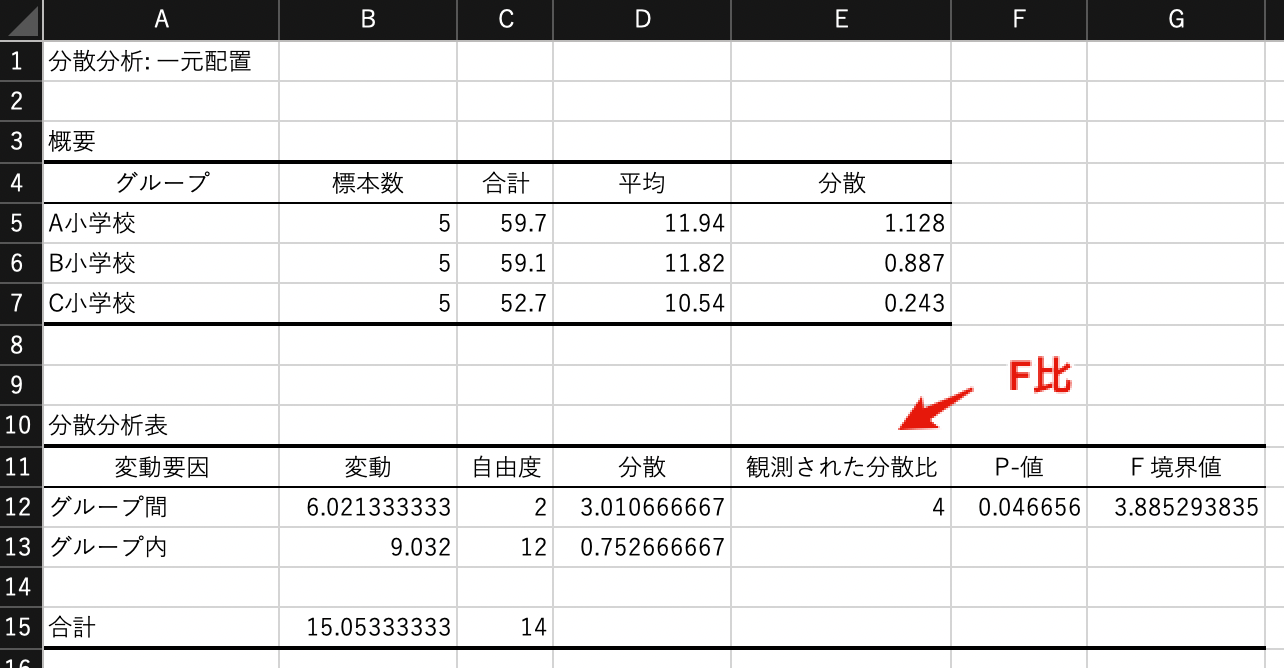
分析ツールから「分散分析: 一元配置」を選びましょう.
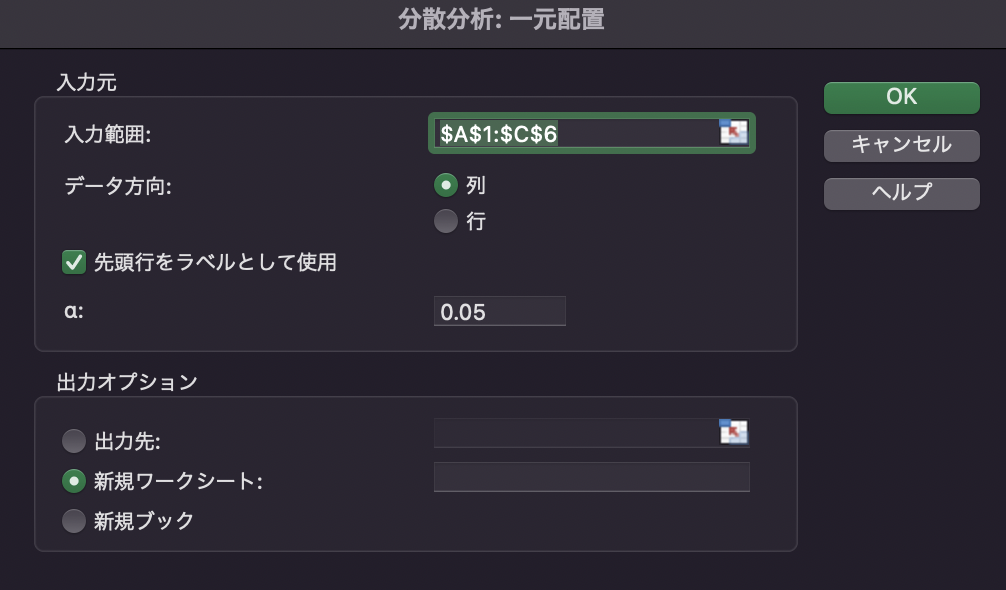
「入力範囲」は$A1:C6$を入力し,「先頭行をラベルとして使用」にチェックを入れます. 「有意水準$\alpha$」は0.05(5%)に設定します.
次のような結果が算出されます. 「観測された分散比」がF比を表しており,$4$となることがわかります. また,群間の自由度は2,群内の自由度が12であることも示されています. さらに,棄却域は$F>3.89$であり,P値は$0.047$となっています. この結果,$0.047 < \alpha=0.05$であることから,帰無仮説は棄却され,3群間で 有意差がある とみなすことになります.
PythonでANOVA
Pythonを利用してANOVAを試してみましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter7.ipynb とします.
pandas,matplotlib,numpyなどのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset6.csv")
display(df)
F比の算出
公式に従ってF比を算出してみましょう.
群間平方和
効果の分散は次の式で算出できます.
$$ 効果の分散 = \frac{群間平方和}{群間の自由度} $$
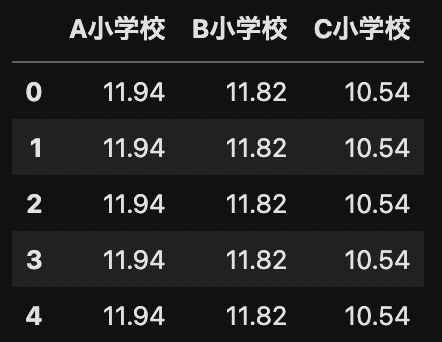
式中の群間平方和は,各群の平均値を期待値とした,ばらつきの大きさです. 最初に各群の平均値を算出します.
mu = df.mean()
mu_df = pd.DataFrame(mu)
mu_df = mu_df.transpose()
display(mu_df)
次に,算出した平均値を期待値と考え,サンプルのデータを期待値に置き換えます.
sn_df = pd.DataFrame()
for i in range(len(df)):
sn_df = pd.concat([sn_df, mu_df])
sn_df = sn_df.reset_index(drop=True)
display(sn_df)
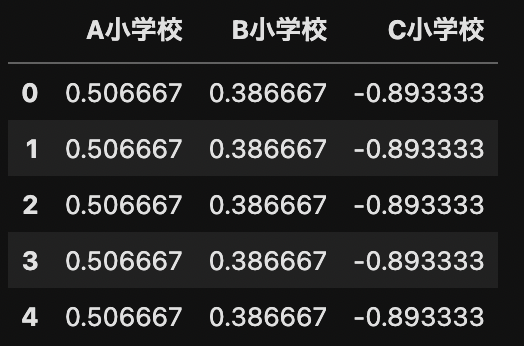
この期待値から,3群全体の平均値を引くことで,相対的な期待値を算出します.
sn_df = sn_df - mu.mean()
display(sn_df)
この相対的な期待値の平方和を算出します. この値が群間平方和を表し,$6.02$となりました.
sn = (sn_df ** 2).sum().sum()
print(sn)
6.021333333333326
群内平方和
誤差の分散は次の式で算出できます.
$$ 誤差の分散 = \frac{群内平方和}{群内の自由度} $$
式中の群内平方和は,元データから各群の平均値を引いた値のばらつきの大きさです.
sd_df = df - mu
display(sd_df)
この値の平方和を算出します. この値が,群内平方和を表し,$9.03$となりました.
sd = (sd_df ** 2).sum().sum()
print(sd)
9.031999999999991
F比
最後にF比を算出します. ここで,群間の自由度は$dfn=3-1=2$,群内の自由度は$dfd=15-3=12$であることに注意してください. この結果,F比は$4.0$となりました. これは,Excelで算出された値と一致しています.
dfn = 2
dfd = 12
f_rate = (sn / dfn) / (sd / dfd)
print(f_rate)
3.9999999999999987
P値の算出
F分布の累積分布はf.cdf関数を利用します.
P値を算出するには,1から累積された確率(面積)を引く必要があることに注意してください.
この結果,P値は$0.047$となりました.
これは,Excelで算出された値と一致しており,$0.047 < \alpha=0.05$であることから,帰無仮説は棄却されます.
from scipy.stats import f
p_value = 1 - f.cdf(4.0, 2, 12)
print(p_value)
0.04665600000000003
f_oneway関数を利用したF比とP値の算出
F比とP値はf_oneway関数を利用して算出することができます.
F比(statistics)は$4.0$,P値は$0.047$になりました.
from scipy.stats import f_oneway
result = f_oneway(df["A小学校"], df["B小学校"], df["C小学校"])
print(result)
F_onewayResult(statistic=4.000000000000006, pvalue=0.04665599999999978)
補足
ANOVAではどの組み合わせの群で有意差があったかは判断できないことから,テューキーの検定 と呼ばれる方法が合わせて用いられることがあります.
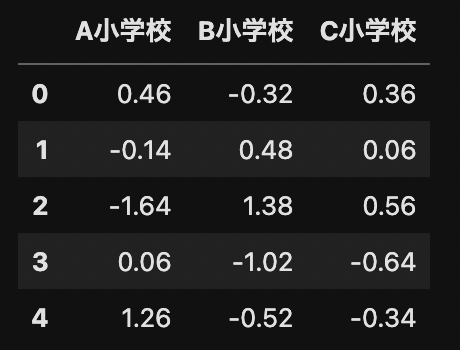
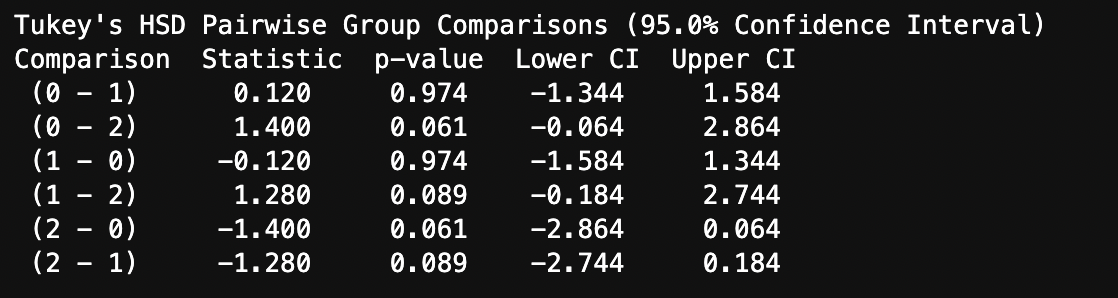
同じデータセットにテューキー検定を適用した結果は次のようになります. 0(A小学校)と2(C小学校)の組み合わせのP値が0.061と最も低く,2群間で傾向が異なる可能性が示唆されました(有意水準5%での有意差は認められないけれど).
from scipy.stats import tukey_hsd
result = tukey_hsd(df["A小学校"], df["B小学校"], df["C小学校"])
print(result)
課題
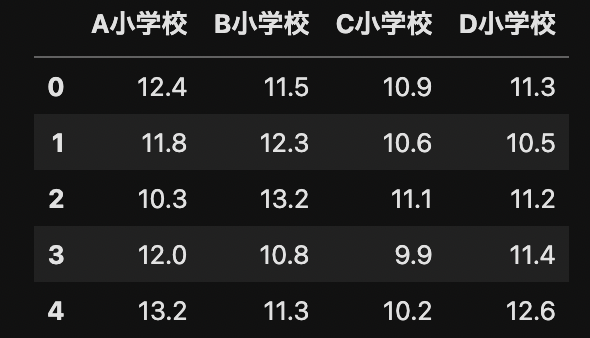
データセットにD小学校のデータを加えて,4群の母集団の平均に有意差があるかANOVAで調べなさい.
df2 = df.assign(D小学校=[11.3, 10.5, 11.2, 11.4, 12.6])
display(df2)
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter7.ipynb としてください.