統計的仮説検定②・t検定(平均値差の検定)
平均値差の検定
前回,母集団とその標本との関係性から仮説を検証するためのt検定を学びました. この他にも,t検定は2つの標本間の関係性から仮説を検証することが可能です(正確には母集団を介して2つの標本の関係性を検証する).
対応のない(独立な)2群のt検定
例えば,ある学校の生徒の50メートル走のタイムを考えます. クラス1からはA,B,C,D,Eの5人,クラス2からはF,G,H,I,Jの5人を抽出し,この2つの標本のタイムの平均が等しいかどうかを検定することができます. これは,対応のない(独立な)2群のt検定 と呼ばれます.
| 生徒 | タイム |
|---|---|
| A | 12.4 |
| B | 11.8 |
| C | 10.3 |
| D | 12.0 |
| E | 13.2 |
| 生徒 | タイム |
|---|---|
| F | 13.1 |
| G | 10.9 |
| H | 12.5 |
| I | 11.3 |
| J | 12.8 |
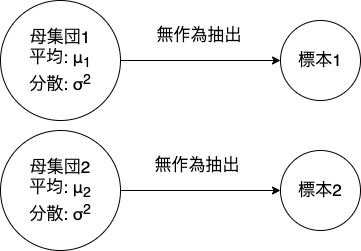
この検定では,クラス1の標本とクラス2の標本が異なる母集団から無作為抽出されたと考え,標本平均$\bar{X}_1$と$\bar{X}_2$の差が次の正規分布に従うことを利用します.
$$ \bar{X}_1 - \bar{X}_2 \sim N\left( \mu_1 - \mu_2, \sigma^2 \left( \frac{1}{n_1} + \frac{1}{n_2} \right) \right) $$
このとき,クラス1の母集団の平均は$\mu_1$,クラス2の母集団の平均は$\mu_2$です.また,分散は等質であることを前提とし同一の$\sigma^2$を用います(分散の等質性が認められない場合はt検定ではなく Welchの検定 を用いる).
これを標準化すると平均0,分散1の標準正規分布に従うことになります(ここまではZ検定).
$$ \frac{\bar{X}_1 - \bar{X}_2 - (\mu_1 - \mu_2)}{\sigma \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim N \left(0, 1 \right) $$
しかし,母集団の分散$\sigma^2$は一般には不明であるため,標本の不偏分散$\hat{\sigma}^2_1$と$\hat{\sigma}^2_2$を用いて,プールした分散$\hat{\sigma}^2$ を算出し,代わりに用います.
$$ \hat{\sigma}^2 = \frac{(n_1 - 1) \hat{\sigma}^2_1 + (n_2 - 1) \hat{\sigma}^2_2}{n_1 + n_2 - 2} $$
プールした分散$\hat{\sigma}^2$を用いることで,自由度$n_1 + n_2 - 2$のt分布に従うことになり,これを検定統計量$t$とします. このとき,帰無仮説は$\mu_1=\mu_2$(母集団の平均に差はない)となることから,検定統計量$t$の分子は$\bar{X}_1 - \bar{X}_2$となります.
$$ t = \frac{\bar{X}_1 - \bar{X}_2 - (\mu_1 - \mu_2)}{\hat{\sigma} \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} = \frac{\bar{X}_1 - \bar{X}_2}{\hat{\sigma} \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} $$
対応のある2群のt検定
足が早くなる薬があったとして,A,B,C,D,Eの薬を飲む前のタイムの平均と,薬を飲んだ後のタイムの平均が等しいかどうかを検定することができます. これは,対応のある2群のt検定 と呼ばれます.
| 生徒 | タイム(薬を飲む前) | タイム(薬を飲んだ後) |
|---|---|---|
| A | 12.4 | 11.8 |
| B | 11.8 | 11.5 |
| C | 10.3 | 10.4 |
| D | 12.0 | 12.0 |
| E | 13.2 | 12.8 |
この検定では,スコアの変化量$D=X_2 - X_1$に着目します.
| 生徒 | D(変化量) |
|---|---|
| A | -0.6 |
| B | -0.3 |
| C | +0.1 |
| D | 0.0 |
| E | -0.4 |
このとき,変化量の平均$\bar{D}$と,標本平均$\bar{X}_1$と$\bar{X}_2$においても関係は維持され,$\bar{D} = \bar{X}_2 - \bar{X}_1$となります. 変化量$D$が平均$\mu_D$,分散$\sigma^2_D$の正規分布に従うとき,変化量の平均$\bar{D}$は平均$\mu_D$,分散$\frac{\sigma^2_D}{n}$の正規分布に従います.
$$ \bar{D} \sim N \left( \mu_D, \frac{\sigma^2_D}{n} \right) $$
これを標準化すると平均0,分散1の標準正規分布に従うことになります(ここまではZ検定).
$$ Z = \frac{\bar{D} - \mu_D}{\sigma_D / \sqrt{n}} \sim N \left( 0, 1 \right) $$
しかし,母集団の分散$\sigma_D^2$は一般には不明であるため,標本の変化量の不偏分散$\hat{\sigma_D}$を代わりに用います. 不偏分散$\hat{\sigma}_D$を用いることで,自由度$n-1$のt分布に従うことになり,これを検定統計量$t$とします. このとき,帰無仮説は$\mu_D=0$(母集団の平均は0)となることから,検定統計量$t$の分子は$\bar{D}$となります.
$$ t = \frac{\bar{D} - \mu_D}{\hat{\sigma}_D / \sqrt{n}} = \frac{\bar{D}}{\hat{\sigma}_D / \sqrt{n}} $$
データセット
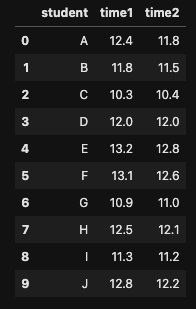
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. ある小学校の生徒の50メートル走のタイムです.
student,time1,time2
A,12.4,11.8
B,11.8,11.5
C,10.3,10.4
D,12,12
E,13.2,12.8
F,13.1,12.6
G,10.9,11.0
H,12.5,12.1
I ,11.3,11.2
J,12.8,12.2
Excelでt検定
Excelの分析ツールを利用して「対応のないt検定」を試してみましょう. ダウンロードしたファイルをExcelで開いてください.
標本の抽出
生徒A〜Eのタイム1を標本1,生徒F〜Jのタイム1を標本2として抽出します(サンプルサイズ$n=5$). 標本1は$E2:E6$,標本2は$F2:F6$に入力しましょう.
仮説
2つの標本が同じ母集団に属することを帰無仮説に置きます.
帰無仮説: 「$\mu_1=\mu_2$(標本が属する母集団の平均は等しい)」
対立仮説: 「$\mu_1 \neq \mu_2$(標本が属する母集団の平均は等しくない)」
分析ツール
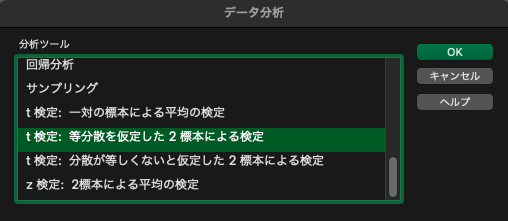
分析ツールから「t検定: 等分散を仮定した2標本による検定」を選びましょう.
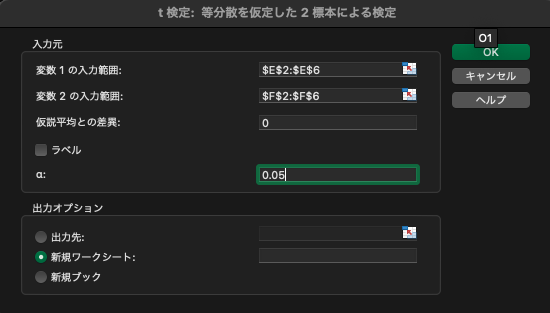
「変数1の入力範囲」は$E2:E6$,「変数2の入力範囲」は$F2:F6$を指定します. ここでは2つの標本の母集団の平均が等しいことを検定するため,「仮説平均との差異」は0に設定します. 「有意水準$\alpha$」は0.05(5%)に設定します.
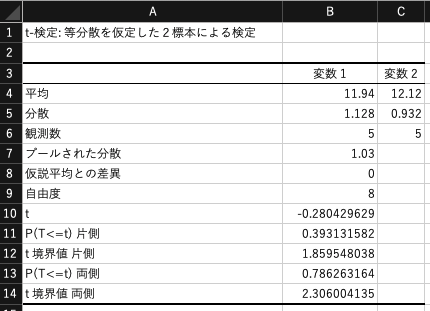
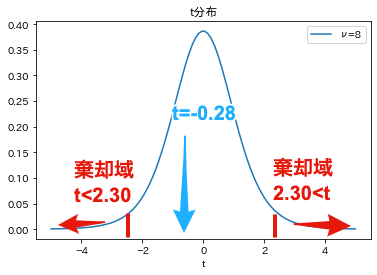
次のような結果が算出されます. t値は-0.28となることがわかります. また,t分布の自由度は$n_1+n_2-2=5+5-2=8$であり,有意水準$\alpha=0.5$(5%)のときの棄却域は$t<-2.31$と$2.31<t$となることがわかります.
この結果,$t=-0.28$は棄却域に含まれないため,帰無仮説である「$\mu_1=\mu_2$(標本が属する母集団の平均は等しい)」は棄却できません. つまり,2つの標本は同じ母集団に所属しており,有意差はない とみなすことになります.
Pythonでt検定
Pythonを利用して「対応のあるt検定」を試してみましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter6.ipynb とします.
pandas,matplotlib,numpy,randomなどのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import random
import numpy as np
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset5.csv")
display(df)
標本の抽出
タイム1を標本1,タイム2を標本2として抽出します(サンプルサイズ$n=10$)
sample1 = df["time1"]
sample2 = df["time2"]
仮説
変化量の母集団の平均が0となることを帰無仮説に置きます.
帰無仮説: 「$\mu =0 $(変化量の母集団の平均は0である)」
対立仮説: 「$\mu \neq 0$(変化量の母集団の平均は0ではない)」
t値の算出
「対応のあるt検定」はst.ttest_rel関数を利用します(デフォルトで両側検定).
算出されたt値は3.10になりました.
import scipy.stats as st
result = st.ttest_rel(sample1, sample2)
t_value = result.statistic
p_value = result.pvalue
print(f"t_value={t_value} p_value={p_value}")
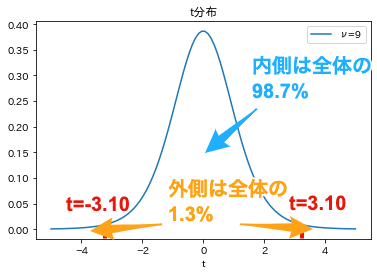
前回求めたように自由度$n-1=9$のt分布における,有意水準$\alpha=0.05$(5%)の棄却域は$t<-2.26$と$2.26<t$であることから,帰無仮説である「$\mu =0 $(変化量の母集団の平均は0である)」は棄却され,対立仮説である「$\mu \neq 0$(変化量の母集団の平均は0ではない)」が採択されます. つまり,薬を飲む前後のタイムには有意差が認められるということになります(この薬には効果があるということ).
t_value=3.103926744219361 p_value=0.012642104381781117
先の結果には,t値だけでなく,p値と呼ばれる指標も算出されています. p値はt分布のグラフにおける,特定のt値の外側となる確率(面積)を表しています. ここでは,$(p = 0.01) < (\alpha= 0.05)$であることから,有意差が認められるという判断をすることもできます.
補足
Pythonで「対応のないt検定」を算出するには,st.ttest_ind関数を利用します.
Pythonで「対応のないt検定(分散の等質性があるとき)」
sample1 = df[0:5]["time1"]
sample2 = df[5:10]["time1"]
st.ttest_ind(sample1, sample2, equal_var=True)
Ttest_indResult(statistic=-0.280429628782387, pvalue=0.7862631640952413)
Pythonで「対応のないt検定(分散の等質性がないとき)」
sample1 = df[0:5]["time1"]
sample2 = df[5:10]["time1"]
st.ttest_ind(sample1, sample2, equal_var=False) # Welchの検定
Ttest_indResult(statistic=-0.28042962878238703, pvalue=0.786326199407499)
課題
生徒A〜Eのタイム2を標本1,生徒F〜Jのタイム2を標本2として抽出し(サンプルサイズ$n=5$),2標本の母集団の平均に有意差があるか,「対応のないt検定(分散の等質性があるとき)」で調べなさい.
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter6.ipynb としてください.