統計的仮説検定①・t検定

t検定

統計的仮説検定 とは，母集団から抽出した標本を利用して，母集団に関する仮説を検証する方法です． 例えば「母集団の平均（母平均）は $\mu$である」などの仮説が考えられます． この仮説を検証するために z検定 や t検定 などと呼ばれる方法が用いられます．

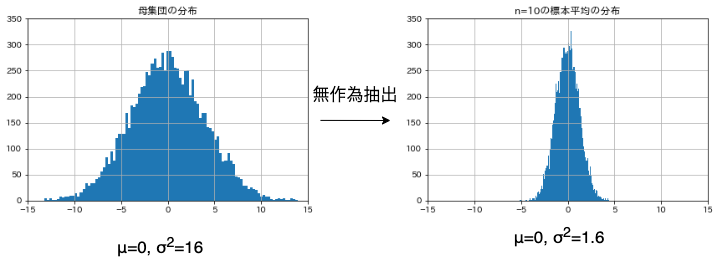
まずは，z検定 について考えていきましょう． z検定は平均$\mu=0$，分散$\sigma^2=1$の正規分布（標準正規分布）を用いる手法です． 平均$\mu$，分散$\sigma^2$の正規分布に従う母集団の分布$X$から， 無作為に抽出した 標本の平均（標本平均） の分布も，正規分布に従うことが知られています． このとき，サンプルサイズ$n$の標本平均$\bar{X}$は，平均$\mu$，分散$\frac{\sigma^2}{n}$の正規分布になります（分散はサンプルサイズに合わせて小さくなることに注意）．

$$ \bar{X} \sim N\left( \mu, \frac{\sigma^2}{n} \right) $$

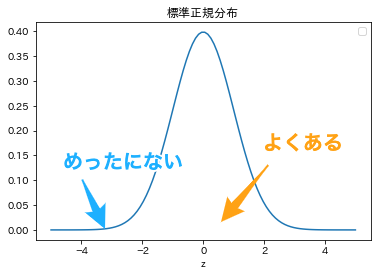
これを標準化すると平均0，分散1の標準正規分布に従うことになり，これを検定統計量$Z$とします． この検定統計量$z$から，その標本が母集団から無作為抽出された標本かどうかを判断することができます．

$$ Z = \frac{\bar{X} - \mu}{\sqrt{\sigma^2 / n}} = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim N\left( 0, 1 \right) $$

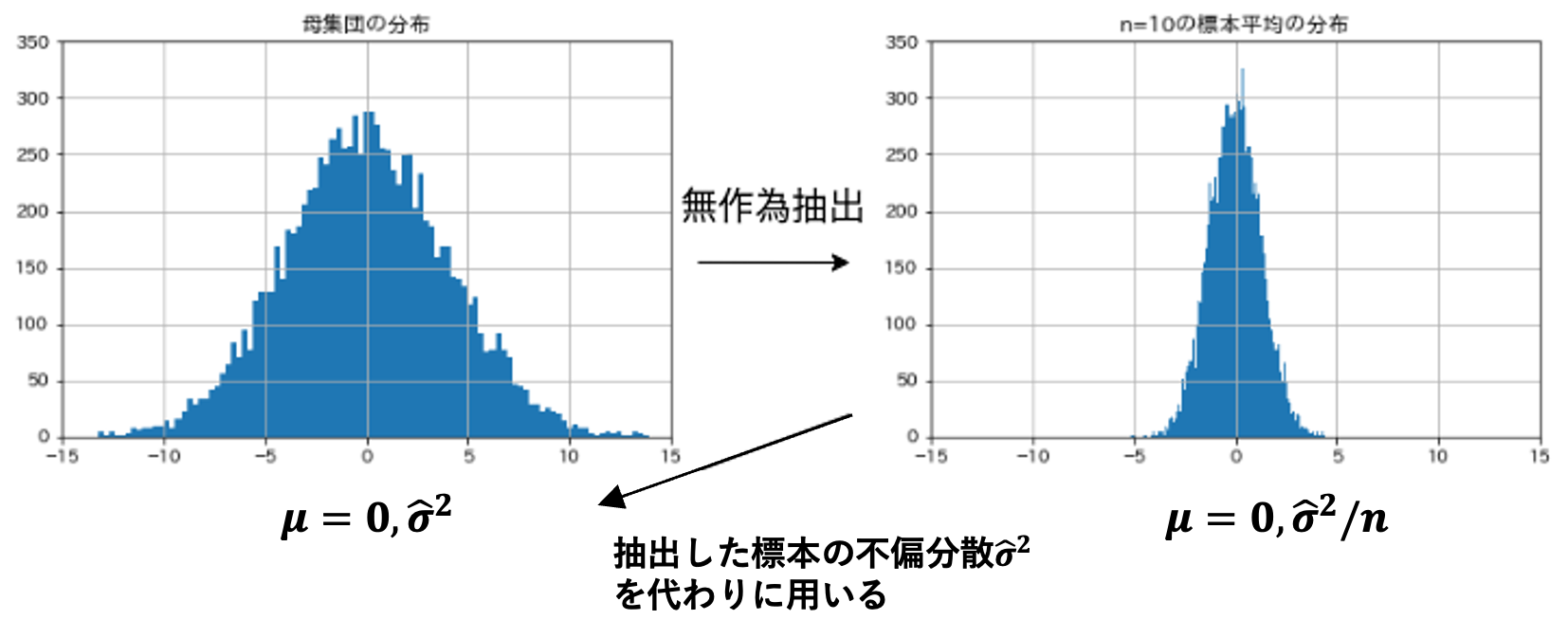
次は，t検定 について考えていきましょう． t検定は母集団の分散$\sigma^2$が分からないときに採用する手法であり，標準正規分布ではなく 自由度を特徴とするt分布 を用います． 一般に母集団の分散は不明であるため z検定 を採用することは稀で，常に t検定 を用いれば良いとされます． 平均$\mu$の正規分布に従う母集団の分布$X$から，無作為に抽出した 標本の平均（標本平均） の分布を考えます． 母集団の分散$\sigma^2$は不明であることから，標本から算出した不偏分散$\hat{\sigma}^2$を代わりに使用します（平方和を$n-1$で割った値）． このとき，サンプルサイズ$n$の標本平均$\bar{X}$は，平均$\mu$，分散$\frac{\hat{\sigma}^2}{n}$の正規分布に従います．

$$ \bar{X} \sim N\left( \mu, \frac{\hat{\sigma}^2}{n} \right) $$

これを標準化すると，自由度$n-1$のt分布に従うことになり，これを検定統計量$t$とします． この検定統計量$t$から，その標本が母集団から無作為抽出された標本かどうかを判断することができます．

$$ t = \frac{\bar{X} - \mu}{\sqrt{\hat{\sigma}^2 / n}} = \frac{\bar{X} - \mu}{\hat{\sigma} / \sqrt{n}} $$

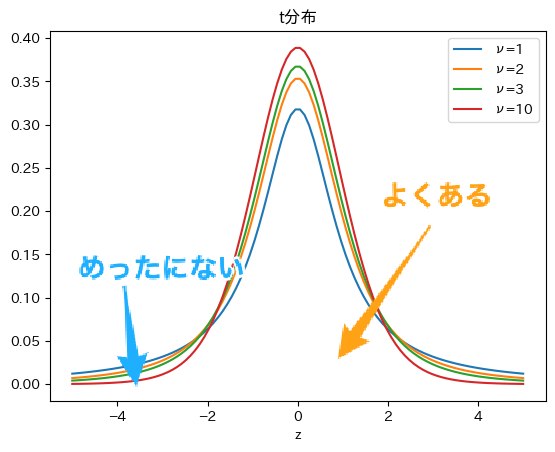
t分布は正規分布と同じような山形の形状をしていますが，自由度と呼ばれるパラメータによって形状が変化するという特徴があります． 自由度はサンプルサイズから1を引いた$n-1$が用いられ，次の図は自由度が$\nu=1,2,3,10$の4通りのt分布を示しています．

データセット

ここでは，次のCSV形式のデータセットを利用します． 下記のURLからファイルをダウンロードしてください． 平均$\mu=30$，分散$\sigma^2=25$（標準偏差$\sigma=5$）の正規分布に従う$N=1000$の母集団のデータです（以降は分散$\sigma^2$は不明とする）．

dataset4.csv

data
34.66035968
25.8226049
27.61256361
30.94129327
43.26588579
~ 省略 ~

Excelでt検定

Exclを利用してt検定を試してみましょう． ダウンロードしたファイルをExcelで開いてください．

標本の抽出

データから$n=10$の標本を無作為抽出し，$D2:D11$に入力しましょう（適当に10のデータを選択すればOK）．

仮説

ここで，仮説を立てます． 仮説は 帰無仮説 と 対立仮説 の2種類で構成されます． 帰無仮説は否定されることを期待して立てる仮説であり， 対立仮説は帰無仮説が棄却された場合に採用される仮説です．

帰無仮説: 「標本が属する母集団の平均は30である（母集団から無作為抽出された標本である）」

対立仮説: 「標本が属する母集団の平均は30ではない（母集団から無作為抽出された標本ではない）」

t値

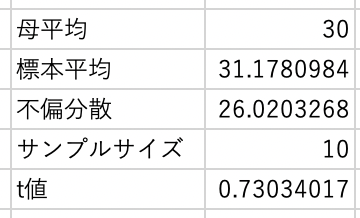
次に，t値を算出するために必要な次の統計値を$D13:D16$に算出します．

• $D13$: 母平均 $\mu=30$
• $D14$: 標本平均 $\bar{x} = 31.2$
• $D15$: 不偏分散 $\hat{\sigma} = 26.0$
• $D16$: サンプルサイズ $n=10$

これらの値を用いてt値を$D17$に算出します． ここで，$SQRT$関数は平方根を表しています． 算出したt値は0.73になりました．

$$ =(D14-D13) / SQRT(D15/D16) $$

有意水準

ここで，有意水準$\alpha$を考えます． 有意水準は，仮説を棄却するための基準であり，一般に$\alpha=0.05$（5%），または，$\alpha=0.01$（1%）が設定されます． ここでは，有意水準を$\alpha=0.05$（5%）に設定することにしましょう．

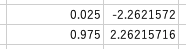
自由度$n-1=9$のt分布における有意水準$\alpha=0.05$(5%)となる棄却域を探します． 今回の仮説は両側検定であるため，下側確率（面積）が0.025，上側確率（面積）が0.025となるt値をt.inv関数を用いて求めれば良いです． セル$C19$に0.025，セル$C20$に0.975を入力し，$D19$と$D20$にt値を算出します（下側確率0.975は上側確率0.025と同じt値になる）． この結果，棄却域は$t<-2.26$と$2.26<t$となりました．

$$ =T.INV(C19,D16-1) $$

$$ =T.INV(C20,D16-1) $$

この結果，$t=0.73$は棄却域に含まれないため，帰無仮説である「標本が属する母集団の平均は30である（母集団から無作為抽出された標本）」は棄却できません． つまり，平均が30の母集団から，無作為抽出された標本であると考えることが自然であるということになります（$t=0.73$は十分に起こりえるということ）．

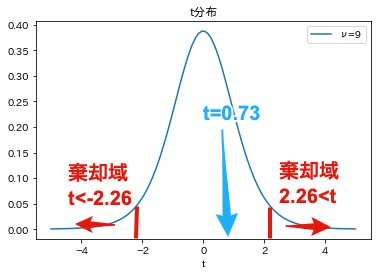
上記の結果を自由度$9$のt分布のグラフでも確認しましょう． 両側検定の有意水準$\alpha=0.05$（5%）とするとき，棄却域はt分布の左側と右側に設定されます． 母集団の平均が30であるとき，この棄却域にt値が含まれることは，非常に珍しいことであることがわかります． 一方で，$t=0.73$は，平均に近く，十分に起こりえるということがわかります．

Pythonでt検定

Pythonを利用してt検定を試してみましょう． Jupyter Labを起動して，Python 3のノートブックを開きます． ノートブックの名前は chapter5.ipynb とします． pandas，matplotlib，numpy，randomなどのライブラリをインポートしておきましょう．

import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
import random

データセットの読込

read_csv関数でデータセットを読み込みます．

df = pd.read_csv("dataset4.csv")
display(df)

標本の抽出

データから作為的に値の大きなデータだけを抽出しましょう． 最初に$n=1000$のデータから，上位の$n=500$のデータをフィルタします．

df_top500 = df.sort_values("data", ascending=False)[0:500].reset_index(drop=True)
display(df_top500)

ここから，$n=10$の標本を無作為抽出します．

sample = random.choices(df_top500["data"], k=10)
print(sample)

[31.72626387, 36.64436813, 30.302818, 34.48227982, 31.60466708, 31.83436782, 38.40457351, 34.24925925, 30.28207168, 31.46033727]

仮説

ここで，仮説を立てます． Excelと同じ帰無仮説と対立仮説です．

帰無仮説: 「標本が属する母集団の平均は30である（母集団から無作為抽出された標本である）」

対立仮説: 「標本が属する母集団の平均は30ではない（母集団から無作為抽出された標本ではない）」

t値

次に，t値を算出するために必要な統計値を算出します．

population_mu = 30 # 母平均
sample_mu = np.mean(sample) # 標本平均
sample_sigma = np.var(sample) # 不偏分散
sample_size = len(sample) # サンプルサイズ
print(population_mu)
print(sample_mu)
print(sample_sigma)
print(sample_size)

30
33.099100643
6.811096913750077
10

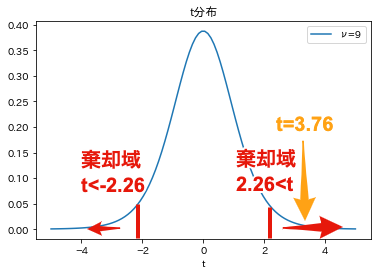
上記の値を利用してt値を算出します． 算出したt値は3.76になりました．

t_value = (sample_mu - population_mu) / np.sqrt(sample_sigma / sample_size)
print(t_value)

3.755148794589911

有意水準

Excelと同じ$\alpha=0.05$（5%）に設定し，棄却域をt.ppf関数で算出します． 棄却域は$t<-2.26$と$2.26<t$となりました．

from scipy.stats import t
print(t.ppf(0.025, sample_size-1))
print(t.ppf(0.975, sample_size-1))

-2.262157162740992
2.2621571627409915

この結果，$t=3.76$は棄却域に含まれるため，帰無仮説である「標本が属する母集団の平均は30である（母集団から無作為抽出された標本）」は棄却され，対立仮説である「標本が属する母集団の平均は30ではない（母集団から無作為抽出された標本ではない）」が採択されます． つまり，平均30の母集団から抽出された標本とは考えにくいということになります（t=3.76はめったに起こらないということ）．

最後にt分布のグラフを描いて確認しましょう． t分布の確率密度はt.pdf関数で算出することができます．

height_list = np.linspace(-5, 5, 100)
density_list = t.pdf(height_list, 9)
df_t = pd.DataFrame({"height":height_list, "density":density_list})
df_t.plot(x="height", y=["density"])
plt.xlabel("t")
plt.legend(["ν=9"])
plt.title("t分布")

課題

次の$n=10$の標本が，平均30の母集団から無作為抽出されたかどうか，有意水準$\alpha=0.05$（5%）のt検定で調べなさい． また，マークダウン・セルを利用して，算出したt値 と 検定の結果 を記述してください．

sample = [27.11716496, 25.89978737, 26.56217535, 29.82681149, 24.5568172, 22.88629043, 17.13597224, 29.64042239, 25.15696187, 26.1132949]

Jupyter Labで作成したノートブックを保存し，ダウンロードして提出してください． ノートブックをダウンロードするには，メニューから Download を選択します． ノートブックのファイル名は chapter5.ipynb としてください．