Pythonを利用した統計処理③・正規分布
正規分布
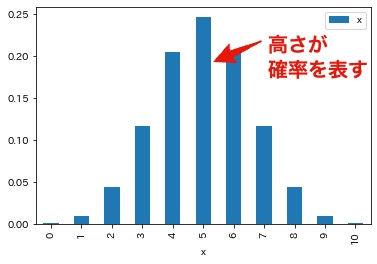
正規分布(ガウス分布) は,前回の 2項分布 と同じ確率分布の一つです. 正規分布は平均に近い値が高い確率で発生し,平均から遠い値が生じる確率は低いという特徴があります. 自然現象や社会現象において,正規分布は多数存在すると言われており,動物の身長・体重,降雨量・雨粒の大きさなどは,正規分布に従っていると考えることができます.
正規分布と2項分布との大きな違いは,2項分布は 離散確率分布 であるのに対し,正規分布は 連続確率分布 であるということです. 離散確率分布では,試行の繰り返しの結果,生じる値は離散値となります. 例えば,コインを10回投げるという試行の結果は,$x=0$から$x=10$までの11通りの値しか存在しません. このため11通りの生起確率を全て合計すると$1$(100%)になります.
$$ \sum_{x=0}^{10} P(x) = P(0) + P(1) + \cdots + P(10) = 1 $$
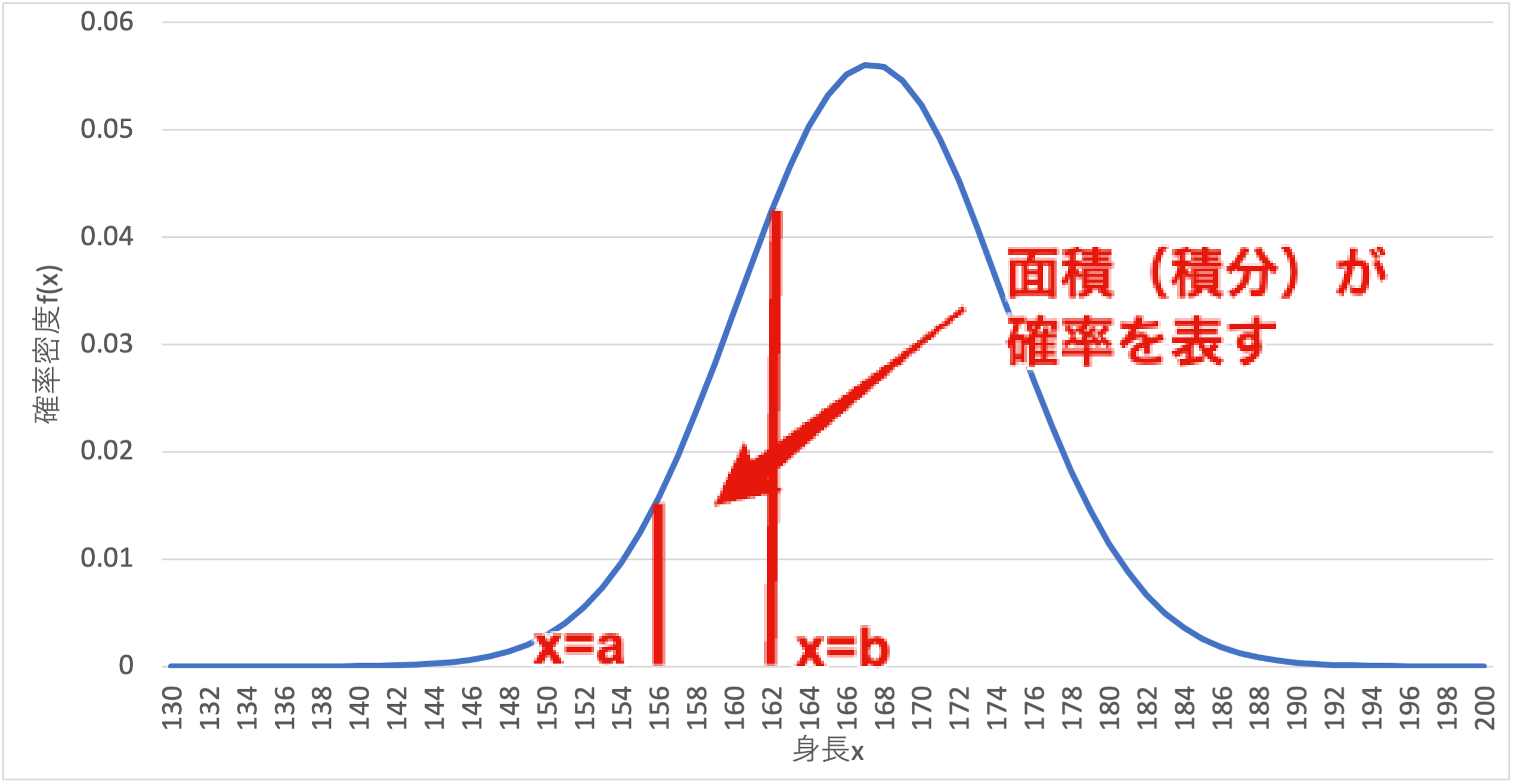
一方,連続確率分布 では,生じる値は連続値となります. 例えば,人間の身長は様々であり,何通りと定めることはできません. このため,連続確率分布では,ある値$x$に対して 確率密度 $f(x)$を定義し, その確率密度の積分で生起確率を表すことになります. 例えば,$a \leq x \leq b$である確率$P(a \leq x \leq b)$は次のように表せます.
$$ P(a \leq x \leq b) = \int_{a}^{b}f(x)dx $$
また,全ての事象の確率密度を積分すると$1$(100%)になります.
$$ P(-\infty \leq x \leq \infty)=\int_{-\infty}^{\infty}f(x)dx = 1 $$
正規分布の確率密度$f(x)$は次の式で求めることができます. ここで,式中の$\mu$は平均,$\sigma^2$は分散です($\sigma$は標準偏差).
$$ f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} exp \left( -\frac{(x - \mu)^2}{2 \sigma^2}\right) $$
データセット
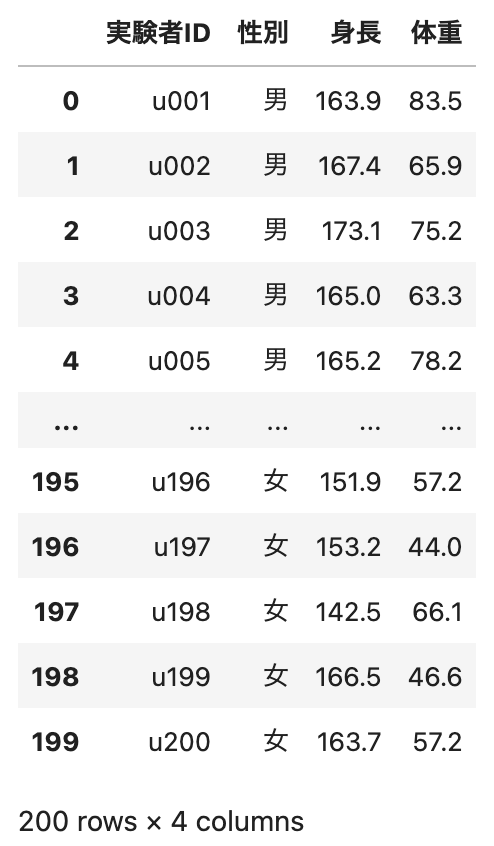
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 日本人の男性100人と女性100人の身長と体重のデータです.
実験者ID,性別,身長,体重
u001,男,163.9,83.5
u002,男,167.4,65.9
u003,男,173.1,75.2
u004,男,165.0,63.3
u005,男,165.2,78.2
~ 省略 ~
Excelで正規分布
Excelを利用して正規分布を算出しましょう. ダウンロードしたファイルをExcelで開いてください.
平均と分散の算出
上述したように正規分布の確率密度を計算するには平均$\mu$と分散$\sigma^2$が必要です.
まずは,男性の身長の平均を,セル$F2$にaverage関数で算出しましょう.
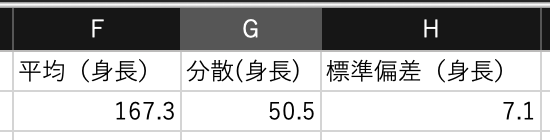
身長の平均は167.3になります.
$$ =average(C2:C101) $$
男性の身長の分散を,セル$G2$にvar関数で算出しましょう.
身長の分散は50.6になります.
$$ =var(C2:C101) $$
男性の身長の標準偏差を,セル$H2$にstdev関数で算出しましょう(標準偏差は分散の平方根でも求まります).
身長の標準偏差は7.1になります.
$$ =stdev(C2:C101) $$
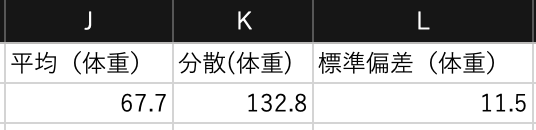
同様に男性の体重に関してもセル$J2$,$K2$,$2$に算出してください. 体重の平均は67.7,分散は132.7,標準偏差は11.5になります.
関数で正規分布
公式に従った正規分布の確率密度をnormdist関数で算出しましょう.
身長$x$,平均$\mu$,標準偏差$\sigma$の確率密度は,$norm.dist(x, \mu, \sigma, FALSE)$と入力します.
身長に関しては$130 \leq x \leq 200$を対象とします.
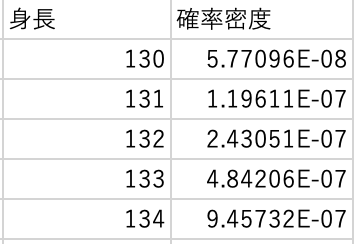
$F5$から$F75$に130〜200を入力し,$G列$にnorm.dist関数で確率密度を計算します.
$$ =norm.dist(F5,$F$2,$H$2,FALSE) $$
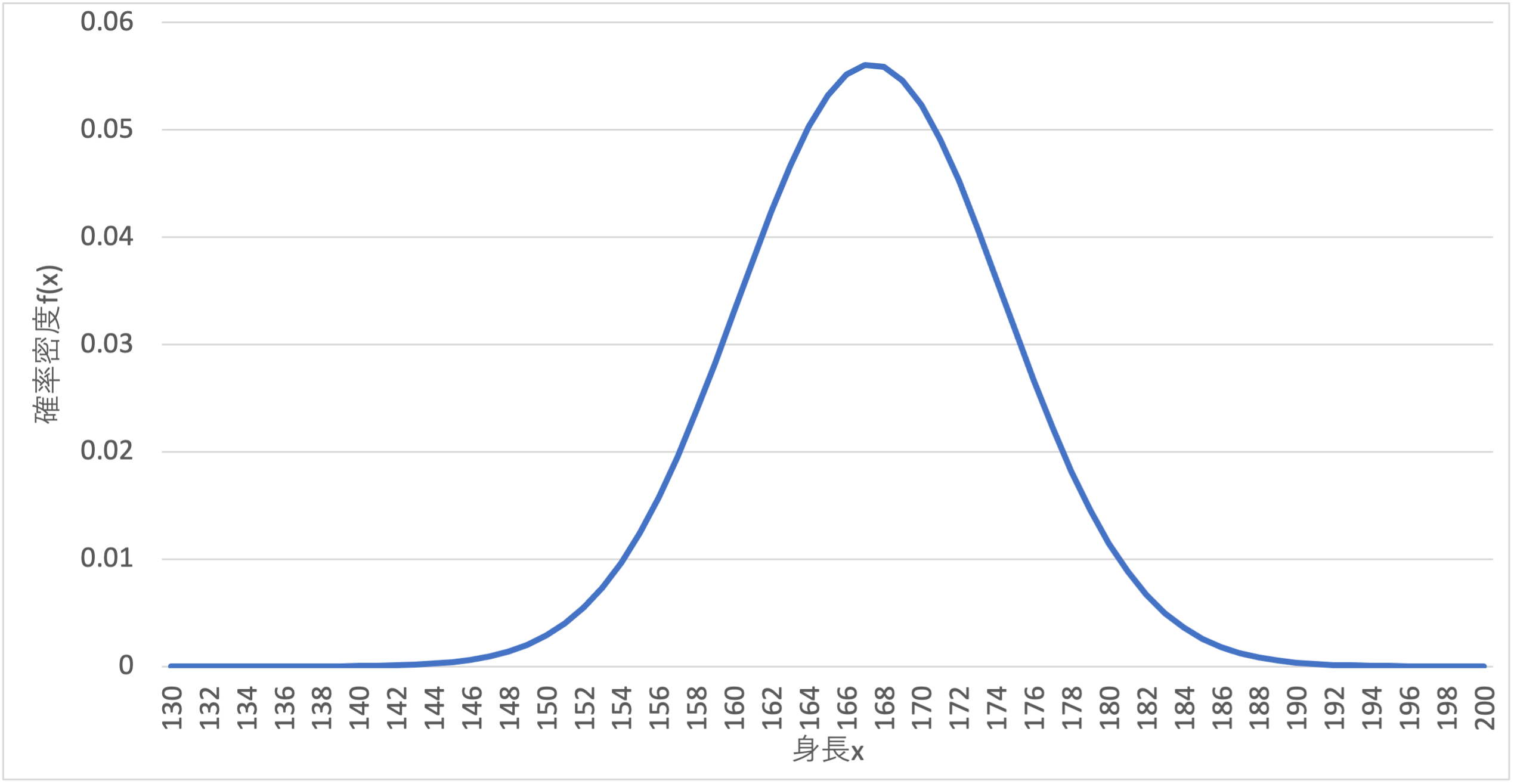
算出した確率密度を折れ線グラフで表すと次のようになります. 平均身長がピークとなった釣鐘状の関数であることがわかります.
体重に関しては$30 \leq x \leq 100$を対象とします.
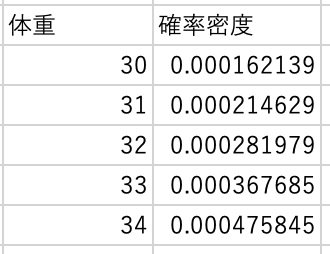
$I5$から$I75$に30〜100を入力し,$J列$にnorm.dist関数で確率密度を計算します.
$$ =norm.dist(I5,$J$2,$L$2,FALSE) $$
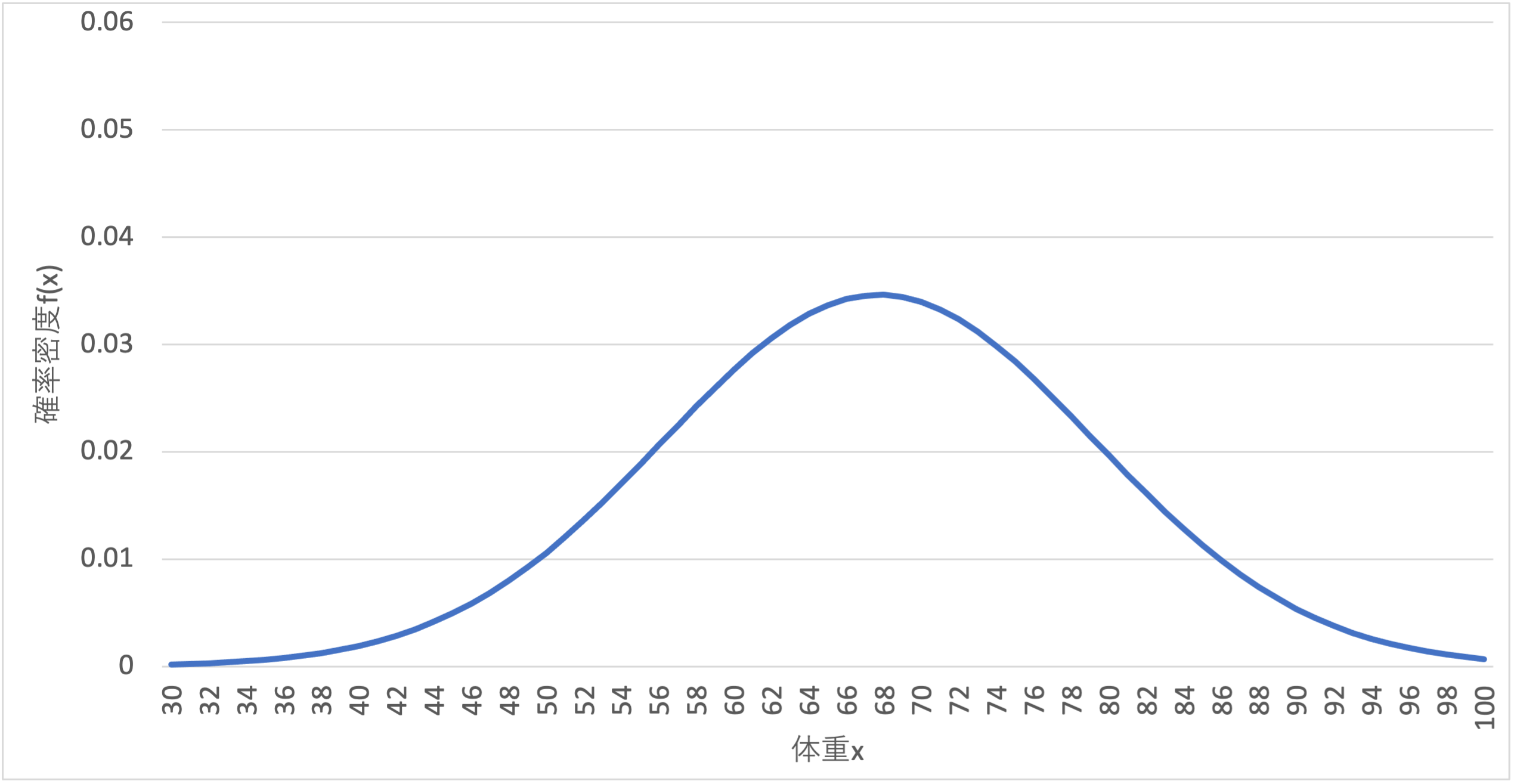
算出した確率密度を折れ線グラフで表すと次のようになります. 身長と同様に平均体重がピークとなった釣鐘状の関数ですが,標準偏差が身長よりも体重の方が大きいため,平べったい形状になっていることがわかります.
Pythonで正規分布
Pythonを利用して正規分布を算出しましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter4.ipynb とします.
pandas,matplotlibのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset3.csv")
display(df)
平均と分散の算出
ここでは,女性の身長と体重の正規分布の確率密度を計算するために,平均$\mu$と分散$\sigma^2$を求めます.
最初にデータフレームから女性のレコードだけを抽出してdf_femaleに代入します.
df_female = df[df["性別"]=="女"]
display(df_female)
女性の身長の平均をmean関数で求めます.
身長の平均は154.7になります.
df_female["身長"].mean()
154.697
女性の身長の分散をvar関数で求めます.
身長の分散は52.0になります.
df_female["身長"].var()
52.00736464646465
女性の身長の標準偏差をstd関数で求めます.
身長の標準偏差は7.2になります.
df_female["身長"].std()
7.21161317920371
同様に女性の体重に関しても算出してください. 体重の平均は56.7,分散は356.9,標準偏差は18.9になります.
関数で正規分布
公式に従った正規分布の確率密度を算出します. 確率密度の計算には,前回と同じように数値計算ライブラリのscipyを利用します.
from scipy.stats import norm
正規分布の確率密度の算出はnorm.pdf関数を利用します.
引数として身長$x=160$,平均$\mu=154.7$,標準偏差$\sigma=7.2$を指定します.
norm.pdf(160, 154.7, 7.2)
この結果,$f(160) \simeq 0.042$となります.
0.04225851769804833
$x=5$だけでなく,$x=130$から$x=200$の範囲で確率密度を計算します.
height_list = list(range(130, 200))
density_list = norm.pdf(height_list, 154.7, 7.2)
print(density_list)
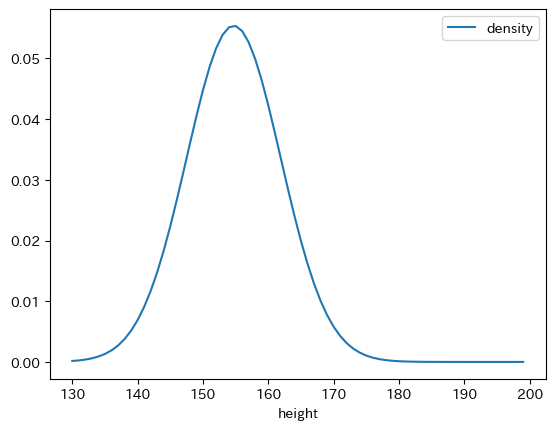
これを折れ線グラフで表すと次の様になります. エクセルのグラフと同様に釣鐘状のグラフになっていることがわかります.
df_norm = pd.DataFrame({"height":height_list, "density":density_list})
df_norm.plot(x="height", y="density")
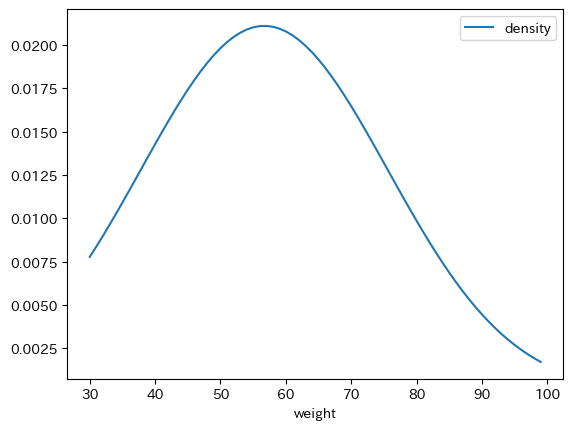
体重に関しても$30 \leq x \leq 100$を範囲として折れ線グラフを描きましょう.
課題
正規分布で確率を求めるには,グラフの面積(積分)を算出する必要があります.
Pythonではcdf関数を利用して求めることができます.
例えば,女性の身長の平均$\mu=154.7$,標準偏差$\sigma=7.2$を利用して,身長が$150 \leq x \leq 160$の範囲にある確率は次の様に計算します.
norm.cdf(160, 154.7, 7.2) - norm.cdf(150, 154.7, 7.2)
この結果,$P(150 \leq x \leq 160) \simeq 0.512$(51.2%)となることがわかります.
0.5122186833519381
上記の方法を利用して,次の確率をPythonで求めなさい.
- 男性の体重が70kg以上である確率
- 女性の体重が40kgから45kgの範囲にある確率
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter4.ipynb としてください.