Pythonを利用した統計処理②・2項分布
2項分布
2項分布 は,コインの表と裏のように結果が2通りとなる試行を, $n$回繰り返したときに,表が出る回数の 確率分布 を表しています. 例えば,コインを投げたときに表が出る確率を$p=1/2$とします. このとき裏が出る確率は$(1-p)=1/2$です.
試行回数$n=1$のときの確率分布は次のようになります. 1回の試行では,表が出る回数は$0$または$1$の2通りです.
| 表が出る回数 | 確率 |
|---|---|
| 0 | 1/2 |
| 1 | 1/2 |
試行回数$n=2$のときの確率分布は次のようになります. 2回の試行では,表が出る回数は$0$,$1$,$2$の3通りです.
| 表が出る回数 | 確率 |
|---|---|
| 0 | 1/4 |
| 1 | 1/2 |
| 2 | 1/4 |
表が出る回数を$x$としたとき,その確率$P(x)$は次の式で求めることができます.
$$ P(x) = {}_nC_x p^x (1-p)^{n-x} $$
例えば,上記の試行回数$n=2$において,表が出る回数$x$の確率は次のように計算します.
$$ P(0) = {}_2C_0 \cdot (1/2)^0 \cdot (1-(1/2))^{2-0} = 1/4 $$
$$ P(1) = {}_2C_1 \cdot (1/2)^1 \cdot (1-(1/2))^{2-1} = 1/2 $$
$$ P(2) = {}_2C_2 \cdot (1/2)^2 \cdot (1-(1/2))^{2-2} = 1/4 $$
データセット
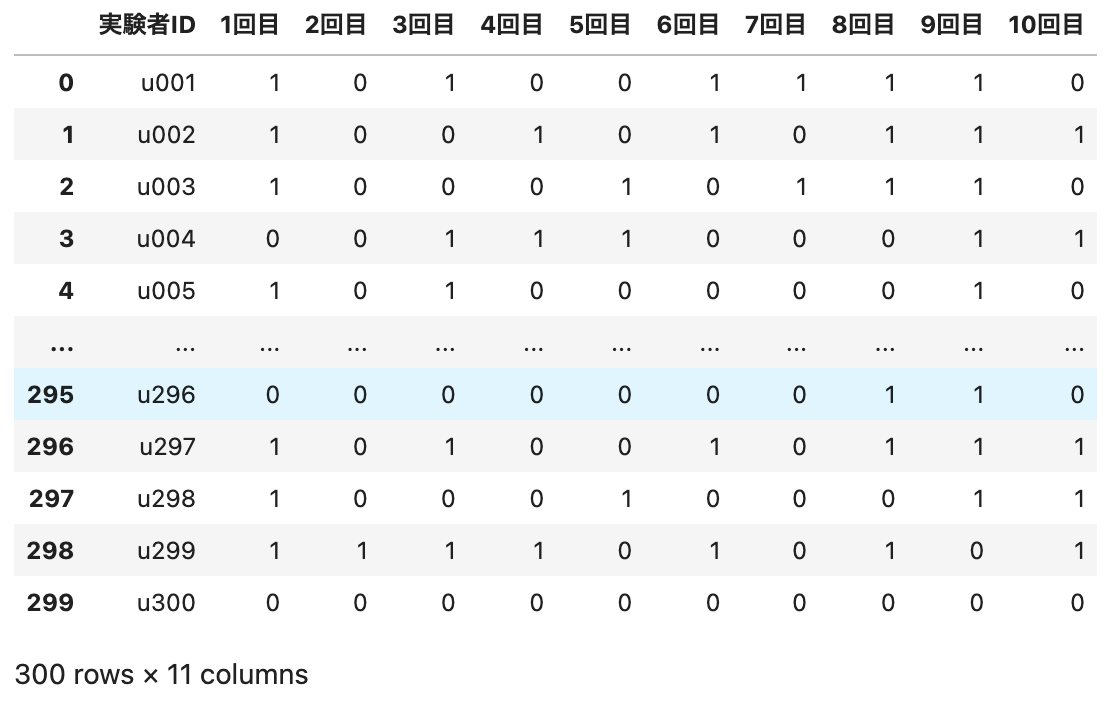
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. $p=1/2$で表が出るコインを$n=10回$投げることを,300人で実験したときのデータです. ここで,試行の結果を,表は$1$,裏は$0$として表していることに注意してください.
実験者ID,1回目,2回目,3回目,4回目,5回目,6回目,7回目,8回目,9回目,10回目
u001,1,0,1,0,0,1,1,1,1,0
u002,1,0,0,1,0,1,0,1,1,1
u003,1,0,0,0,1,0,1,1,1,0
u004,0,0,1,1,1,0,0,0,1,1
u005,1,0,1,0,0,0,0,0,1,0
~ 省略 ~
Excelで2項分布
Excelを利用して2項分布を算出しましょう. ダウンロードしたファイルをExcelで開いてください.
ヒストグラムの作成
最初に表が出る回数$x$のヒストグラムを作成します.
$L$列にsum関数で表が出た回数をカウントします.
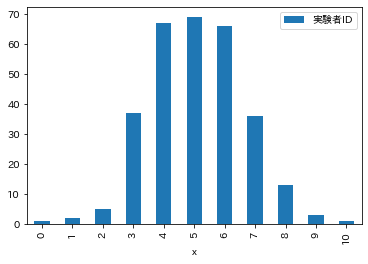
最初の実験ではコインの表が6回出たことがわかります.
$$ =sum(B2:K2) $$
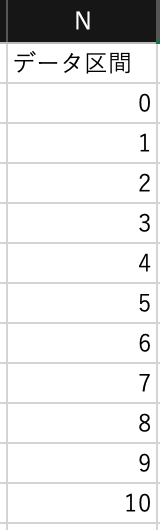
次に$N$列にヒストグラムのデータ区間を入力します. 試行回数は$n=10$であることから,データ区間($x$の取り得る値)は$0$から$10$までの11通りです.
データ・タブの分析ツールから ヒストグラム を選択し,次のように設定します. 入力範囲は$L2:L301$,データ区間は$N2:N12$です.
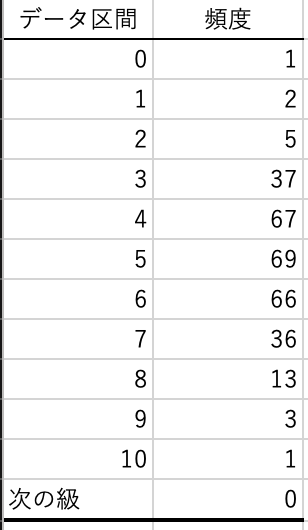
この結果,次のようなヒストグラムが作成されます.
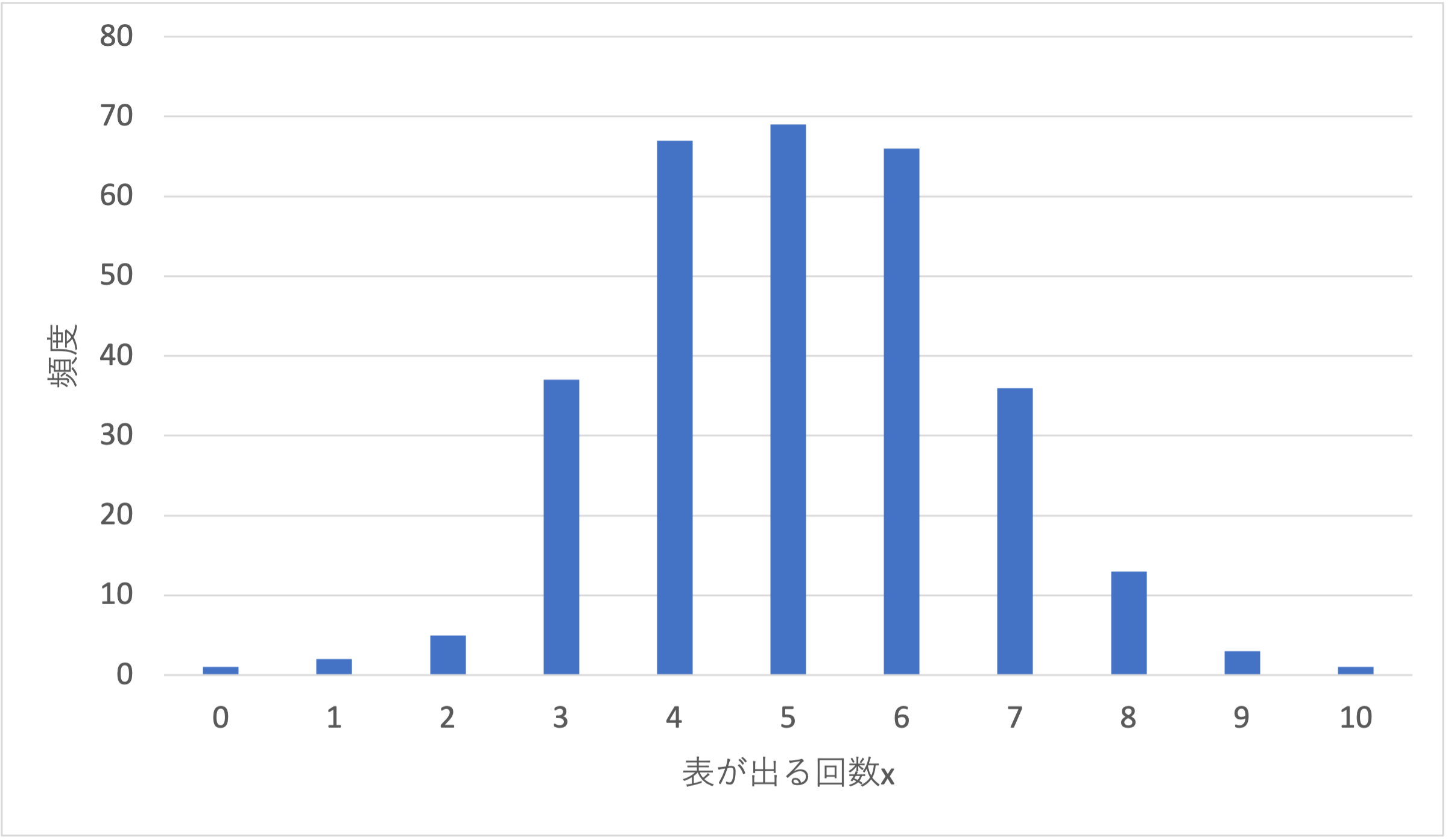
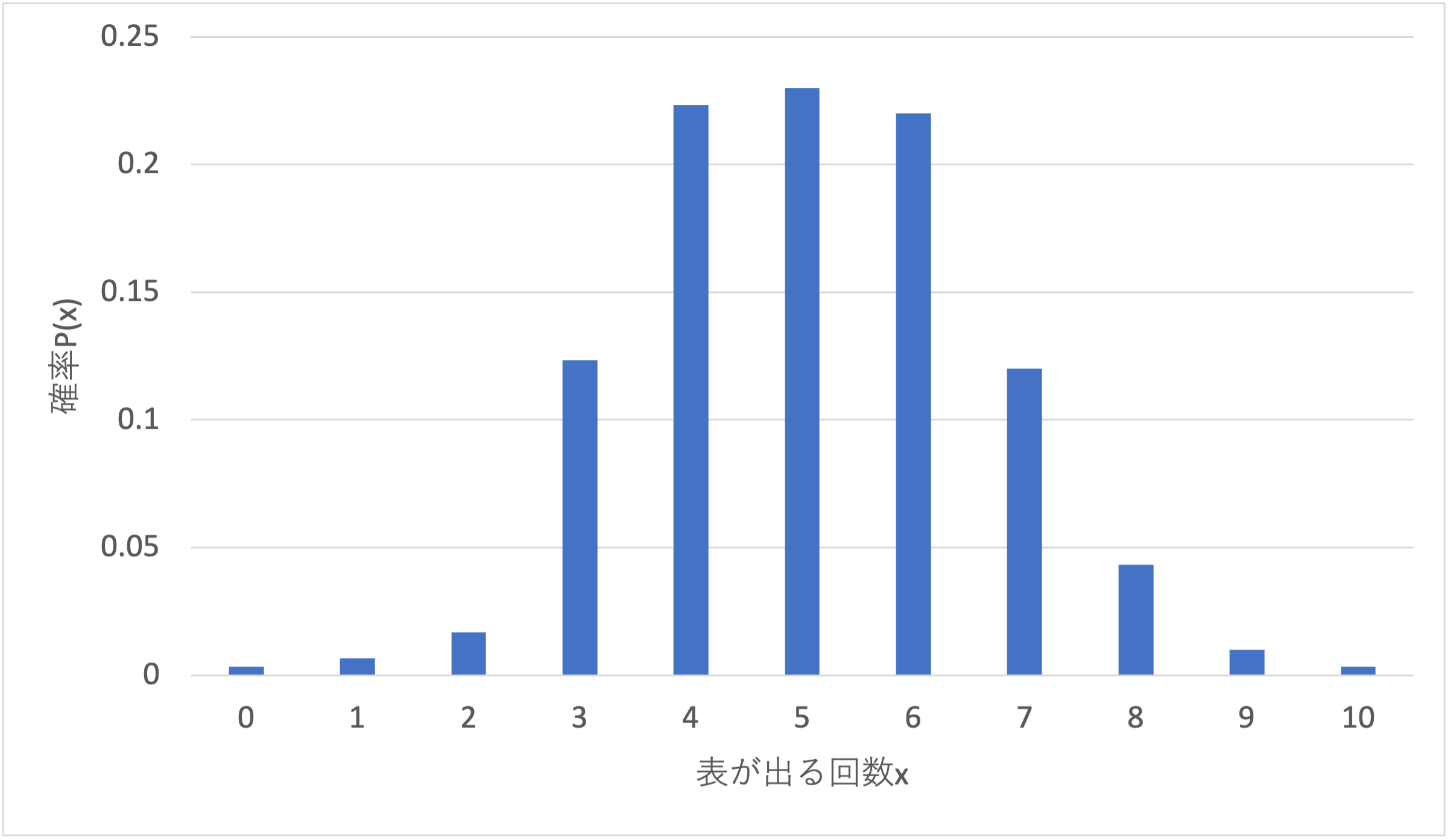
最後にヒストグラムの結果を棒グラフで表しましょう. 横軸は表が出る回数$x$,縦軸は頻度であり,$x=5$が最も高い頻度であることがわかります.
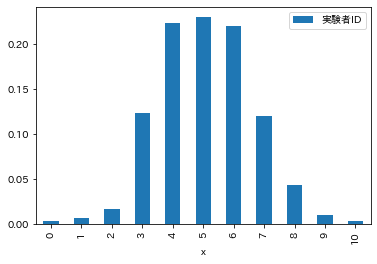
この縦軸の値をサンプル数の300で割り,確率$P(x)$で表すと2項分布となります. $x=5$となる確率は$P(5) \simeq 0.23$であることがわかります.
関数で2項分布
上記の2項分布の確率は,300のサンプルから算出した値です.
公式に従った2項分布の確率は,Excelのbinom.dist関数を利用して算出することが可能です.
表が出る回数$x$,試行回数$n$,表が出る確率$p$の確率は,$binom.dist(x, n, p, FALSE)$で計算します.
例えば,$x=5$,$n=10$,$p=1/2$の確率を計算すると,$P(5) \simeq 0.25$となることがわかります.
$$ =binom.dist(5,10,0.5,FALSE) $$
Pythonで2項分布
Pythonを利用して2項分布を算出しましょう. Jupyter Labを起動して,Python 3 のノートブックを開きます. ノートブックの名前は chapter3.ipynb とします.
データセットの読込
pandasをインポートして,read_csv関数でデータセットを読み込みましょう.
import pandas as pd
df = pd.read_csv("dataset2.csv")
display(df)
ヒストグラムの作成
まずはヒストグラムを作成しましょう.
1回目〜10回目までの,表が出た回数の合計をsum関数で求めます(axis=1は行方向に計算),
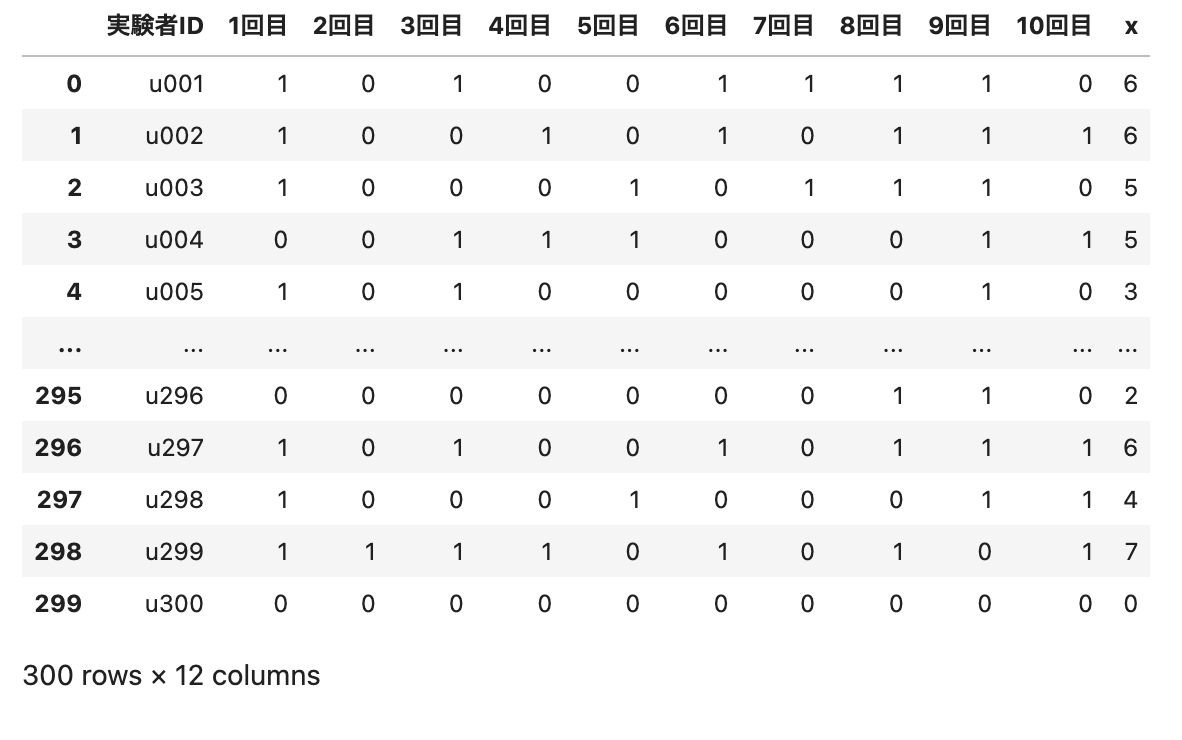
x = df[["1回目","2回目","3回目","4回目","5回目","6回目","7回目","8回目","9回目","10回目"]].sum(axis=1)
算出した合計$x=\{6,6,5,5,3,\cdots\}$を,assign関数でデータフレームの右端に追加します.
df = df.assign(x=x)
display(df)
次に,groupby関数でxの値ごとにグループ集計し,ヒストグラムを作成します.
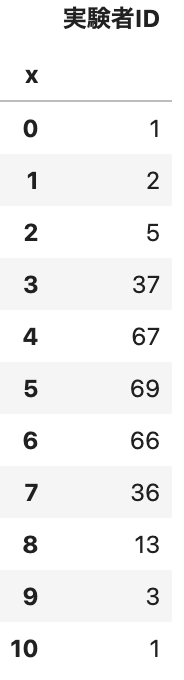
xは0から10までの11通りの値をとります.
集計した結果をdf_histに代入します.
df_hist = df[["x", "実験者ID"]].groupby("x").count()
display(df_hist)
ヒストグラムを棒グラフで表現します. グラフ生成に必要なライブラリであるmatplotlibと japanize_matplotlibをインポートとしておきます.
import matplotlib.pyplot as plt
import japanize_matplotlib
棒グラフを生成するには,plot.bar関数を利用します.
df_hist.plot.bar()
縦軸の頻度を300で割ることで,確率分布として表します. Excelのグラフと一致していることを確認しましょう.
(df_hist / 300).plot.bar()
関数で2項分布
最後に関数を利用して公式に従った2項分布を算出します. 2項分布の確率計算には,数値計算ライブラリのscipyを利用します.
from scipy.stats import binom
2項分布の確率の算出はbinom.pmf関数を利用します.
引数は表が出る回数$x=5$,試行回数$n=10$,表が出る確率$p=0.5$を指定します.
binom.pmf(5, 10, 0.5)
この結果,$P(5) \simeq 0.25$となり,Excelの関数を利用して算出した確率と一致します.
0.24609375000000025
$x=5$だけでなく,11通りある全ての$x$について計算してみます.
x=[0,1,2,3,4,5,6,7,8,9,10]を指定します.
計算結果はdistに代入します.
dist = binom.pmf([0,1,2,3,4,5,6,7,8,9,10], 10, 0.5)
print(dist)
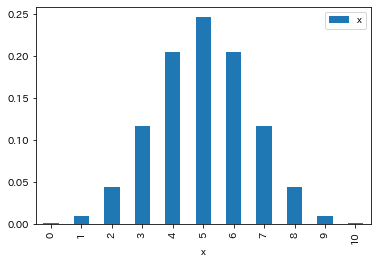
算出された確率分布は次のようになりました.
[0.00097656 0.00976563 0.04394531 0.1171875 0.20507813 0.24609375
0.20507813 0.1171875 0.04394531 0.00976563 0.00097656]
これを棒グラフで表すと次の様になります. 上記で求めた300サンプルの確率分布とよく似ていることがわかります.
df_binom = pd.DataFrame({"x":dist})
df_binom.plot.bar()
plt.xlabel("x")
課題
次の2項分布の確率をPythonで求めなさい.
- 均等な確率で目が出るサイコロを,5回投げて,偶数が3回出る確率
- 1/3の確率で表が出るイカサマのコインを,5回投げて,3回表が出る確率
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter3.ipynb としてください.