Pythonを利用した統計処理①・相関係数
相関係数
相関係数とは2つの変数XとYのの関係性を表す指標です.
例として,X=気温とY=アイスクリームの売上数を考えてみましょう.
気温が高い夏にアイスクリームの売上数は増加し,
逆に気温が低い冬にアイスクリームの売上数は減少すると考えられます.
このような関係を 正の相関 と呼びます.
同様に,X=気温とY=おでんの売上数を考えてみましょう.
気温が高い夏におでんの売上数は減少し,
逆に気温が低い冬におでんの売上数は増加すると考えられます.
このような関係を 負の相関 と呼びます.
この関係性を定量的に表す方法が 相関係数 です.
相関係数の公式を確認しておきましょう. $X=\{x_1, x2, \cdots, x_n\}$,$Y=\{y_1,y_2,\cdots,y_n\}$とします. このとき,$X$と$Y$の相関係数は次の式で求められます.
$$ XとYの相関係数=\frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum (x_i - \bar{x})^2} \cdot \sqrt{\sum (y_i - \bar{y})^2}} $$
算出された相関係数は-1から1の範囲となり,1に近いほど強い正の相関,-1に近いほど強い負の相関となります. また,相関係数が-0.2から0.2の範囲のときは,相関なしとみなすことが一般的です.
| 相関係数 | 相関の強さ |
|---|---|
| 0.7~1.0 | 強い正の相関 |
| 0.4~0.7 | 正の相関 |
| 0.2~0.4 | 弱い正の相関 |
| -0.2~0.2 | 相関なし |
| -0.4~-0.2 | 弱い負の相関 |
| -0.7~-0.4 | 負の相関 |
| -1.0~-0.7 | 強い負の相関 |
データセット
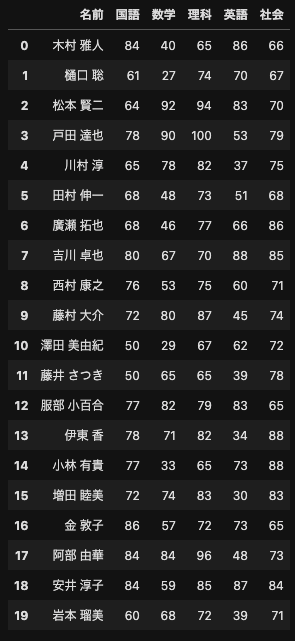
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 生徒20人の5科目のテストの点数に関するデータです.
名前,国語,数学,理科,英語,社会
木村 雅人,84,40,65,86,66
樋口 聡,61,35,74,70,67
松本 賢二,64,92,94,42,70
戸田 達也,78,90,100,53,79
川村 淳,65,78,82,37,75
~ 省略 ~
Excelで相関係数
Excelを利用して相関係数を算出しましょう. ダウンロードしたファイルをExcelで開いてください.
散布図の作成
最初にデータを散布図で確認しましょう. ここでは,「数学と理科」と「数学と英語」の散布図を作成します.
「数学と理科」の散布図を作成するには,
セルC2:C21とD2:D21を選択し,メニューの 散布図 を選択します.
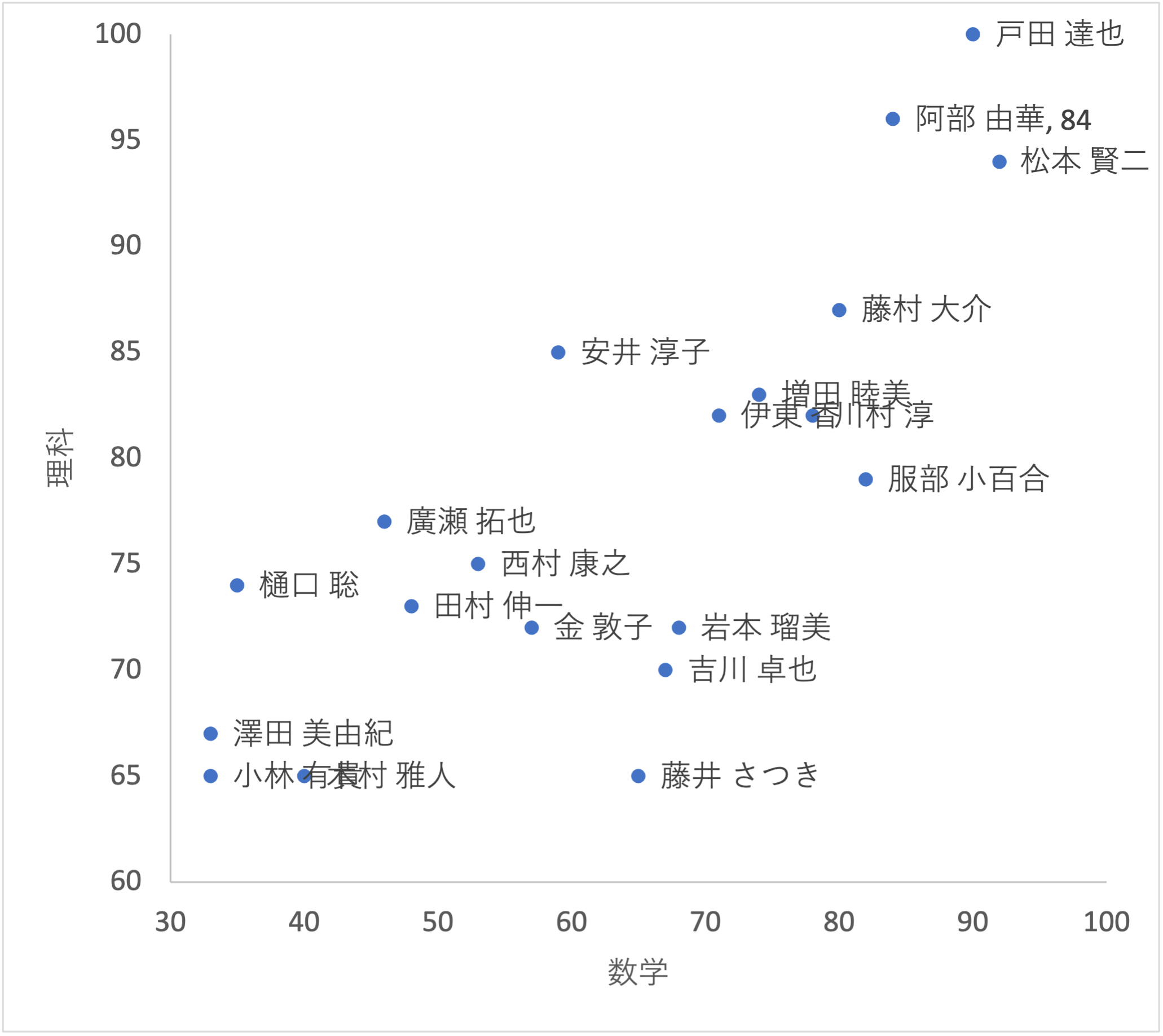
散布図を確認すると,全体的に 右上がり の傾向が確認できます.
これは「数学が得意な人は理科も得意」であることを意味しています.
つまり $X=数学$,$Y=理科$としたとき,$X$と$Y$には 正の相関 があると考えられます.
「数学と英語」の散布図を作成するには,
セルC2:C21とE2:E21を選択し,メニューの 散布図 を選択します.
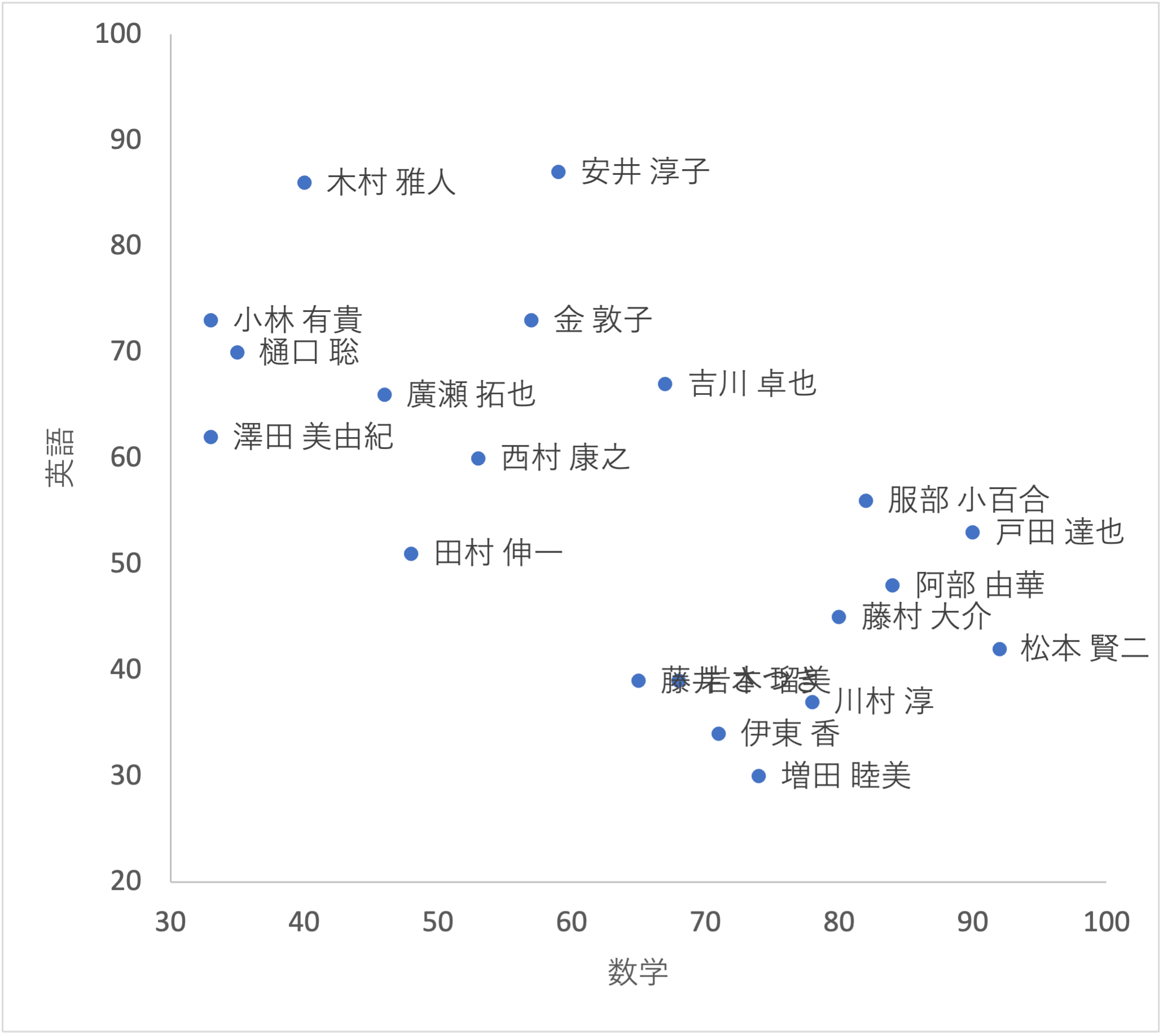
散布図を確認すると,全体的に 右下がり の傾向が確認できます.
これは「数学が得意な人は英語が苦手」であることを意味しています.
つまり $X=数学$,$Y=英語$としたとき,$X$と$Y$には 負の相関 があると考えられます.
相関係数の算出
Excelで相関係数を算出するにはcorrel関数を利用します.
セルB23に「数学と理科」の相関係数を求めましょう.
$$ =CORREL(C2:C21,D2:D21) $$
同様にセルB24に「数学と英語」の相関係数を求めましょう.
$$ =CORREL(C2:C21,E2:E21) $$
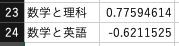
この結果,「数学と理科」の相関係数は約0.78,「数学と英語」の相関係数は約-0.62となりました. よって,「数学と理科」には「強い正の相関」,「数学と英語」には「負の相関」があることが確認できました.
Pythonで相関係数
Pythonを利用して相関係数を算出しましょう. Jupyter Labを起動して,Python 3 のノートブックを開きます. ノートブックの名前は chapter2.ipynb とします.
データセットの読込
PythonでCSV形式のファイルを読み込むには pandasというライブラリ(追加機能)を利用します.
最初に次のコードでpandasの利用を宣言します.
この宣言で,pandasの機能を pd という別名で利用することが可能になります.
import pandas as pd # pandasのインポート
CSV形式のファイルを読み込むにはread_csv関数を利用します.
読み込まれたデータは データフレーム という形式で表され,変数dfに代入されています.
また,データフレームを出力するにはdisplay関数を利用します(print関数でも出力可能).
df = pd.read_csv("dataset1.csv")
display(df)
ここで,データフレームの使い方を確認します.
列方向にデータ抽出
列方向にデータを抽出するにはdf[列名]と記述します.
複数の列を取得する場合は,df[[列名1,列名2]]と記述します.
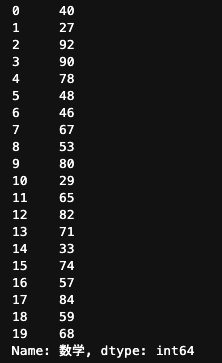
df["数学"]
df[["数学","理科"]]
行方向にデータ抽出
行方向にデータを抽出するにはdf[先頭の行番号:最後の行番号]と記述します.
このとき,最後の行番号のデータは含まれないことに注意してください.
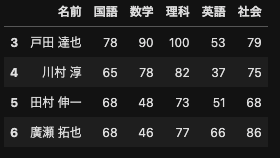
df[3:7]
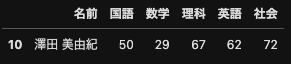
df[10:11]
相関係数の算出
データフレームで相関係数を算出するには corr関数を利用します.
「数学と理科」と「数学と英語」の相関係数を算出します.
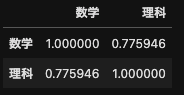
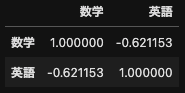
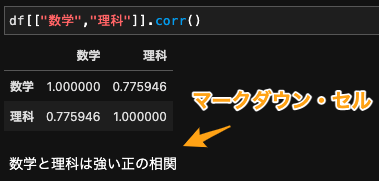
Exceで算出した結果と同じように,「数学と理科」の相関係数は約0.78,「数学と英語」の相関係数は約-0.62となりました.
df[["数学","理科"]].corr()
df[["数学","英語"]].corr()
課題
次の相関係数を調べなさい. また,マークダウン・セル を利用して,それぞれの相関の強さを記述してください.
- 数学と国語の相関係数
- 英語と理科の相関係数
- 国語と英語の相関係数
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter2.ipynb としてください.