フーリエ解析
フーリエ解析
フーリエ解析(Fourier Analysis) は,複雑な関数を周波数成分に分解して解析する手法です. 音,電磁波,光などは波としての特徴を持つことから,フーリエ変換(Fourier Transform) によってsin関数やcos関数に分解することが可能であり,それらの関数の周波数成分の強さも求めることができます.
ここで,波を表すsin関数を次のように定義します. $\omega$は角速度(rad/s)であり,1秒間に進むラジアン角の大きさを表します. 例えば,1秒間に1周期だけ進む場合は$\omega=2 \pi$となります. また,$a$は振幅の最大値を表します.
$$ f(t) = a \cdot sin(\omega t) $$
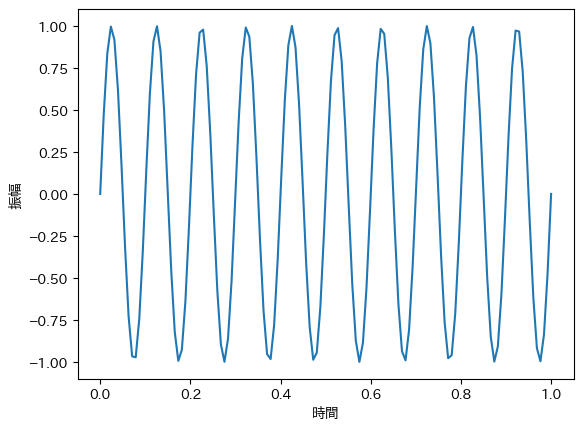
例として,1秒間に10周期のsin関数が含まれる10Hzの波を考えます. このとき,$\omega=10 \cdot 2 \pi$となります. また,振幅の最大値は$a=1$とします.
$$ f(t) = sin(10 \cdot 2 \pi t) = sin(20 \pi t) $$
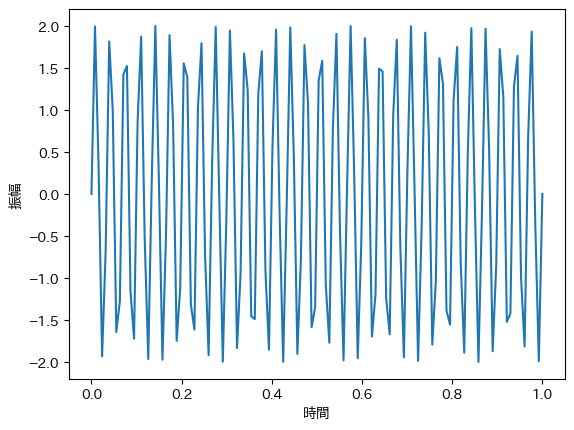
同様に,1秒間に30周期のsin関数が含まれる30Hzの波を考えます. このとき,$\omega=30 \cdot 2 \pi$となります. また,振幅の最大値は$a=2$とします.
$$ f(t) = 2 \cdot sin(30 \cdot 2 \pi t) = 2 \cdot sin(60 \pi t) $$
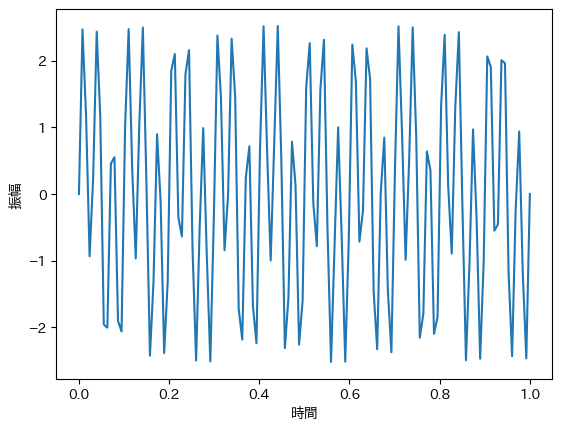
上記の10Hzと30Hzの波を合成すると次のようになります. このように,sin関数やcos関数を合成することで,任意の関数(波)を表現することが可能です.
$$ f(t) = sin(20 \pi t) + 2 \cdot sin(60 \pi t) $$
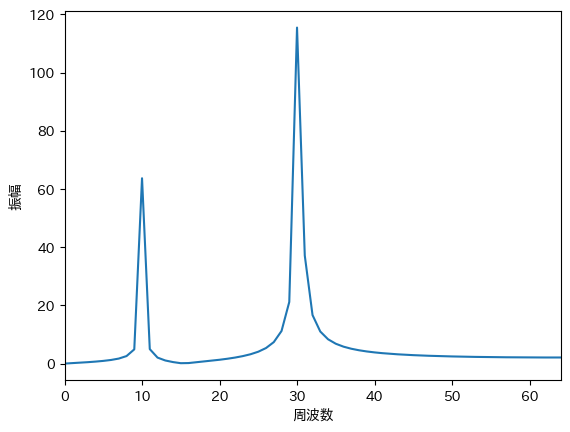
この$f(t)$から,各周波数の振幅を算出するのが フーリエ変換 です. フーリエ変換の結果は次のグラフで表されます. このグラフは パワースペクトル とも呼ばれます. 横軸は周波数であり,10Hzと30Hzの振幅が大きくなっていることがわかります. また,10Hzの振幅に対して,30Hzの振幅が2倍になっていることも確認できます.
先に述べたように音は空気の振動であり波の性質を持ちます. 音の高低(音階)は周波数で決まり,「ド」「レ」「ミ」の周波数は次の表となっています. フーリエ変換して,対応する周波数が取得できるかどうか,後程,確認してみましょう.
| 音階 | 周波数 |
|---|---|
| ド(C4) | 261.63Hz |
| レ(E4) | 293.67Hz |
| ミ(F4) | 329.63Hz |
データセット
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 上記の例で用いた10Hzと30Hzのsin関数を合成したデータです. データ数は$N=128$であり,これは1秒間に128回のサンプリングをしたとこと意味します.
また,魔王魂で提供されているピアノの「ド」「レ」「ミ」の音声ファイルをフーリエ変換して周波数成分を取得してみます. 各音声ファイルをダウンロードしておいてください.
Excelでフーリエ解析
Excelの分析ツールを利用してフーリエ解析を試してみましょう. ダウンロードしたファイルをExcelで開いてください.
分析ツール
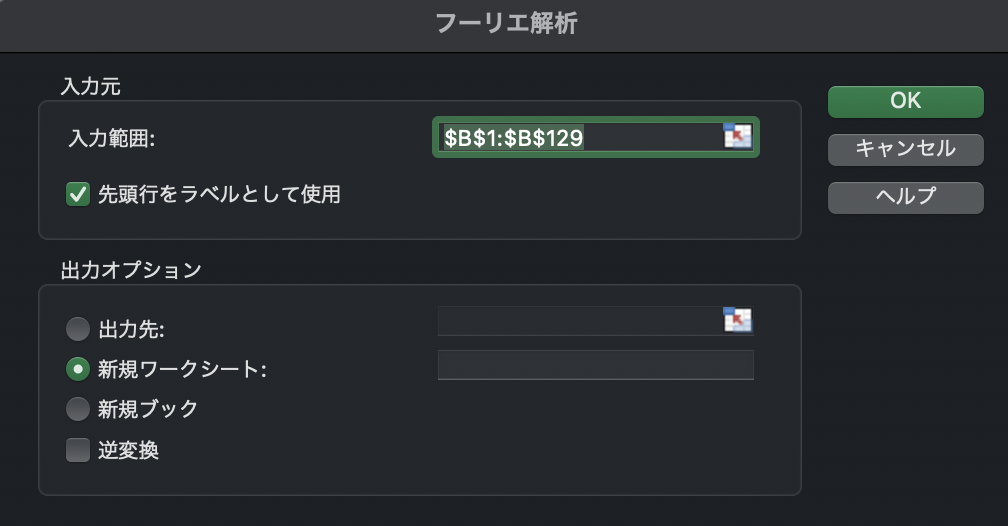
分析ツールから「フーリエ解析」を選びましょう. 入力範囲に$B1:B129$を入力します. このとき,「先頭行をラベルとして使用」にチェックを入れます.
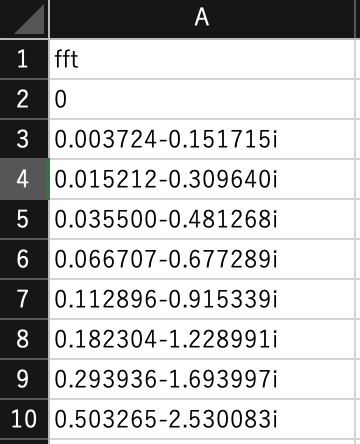
次のような結果が算出されます($A1$には「fft」と入力しておきます).
上記の算出された値は複素数です.
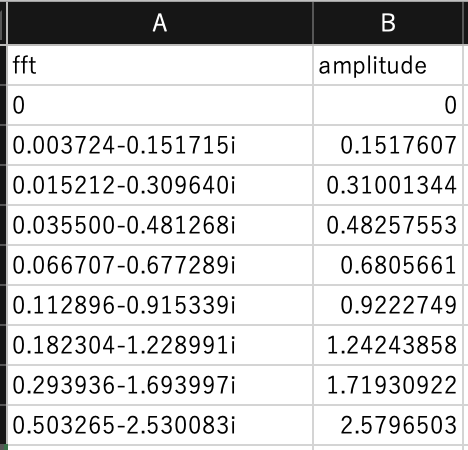
そこで,imabs関数を利用して,B列に振幅を計算します.
データ数$N=128$であることから,0Hzから127Hzまでの周波数に対する振幅が求められることになります.
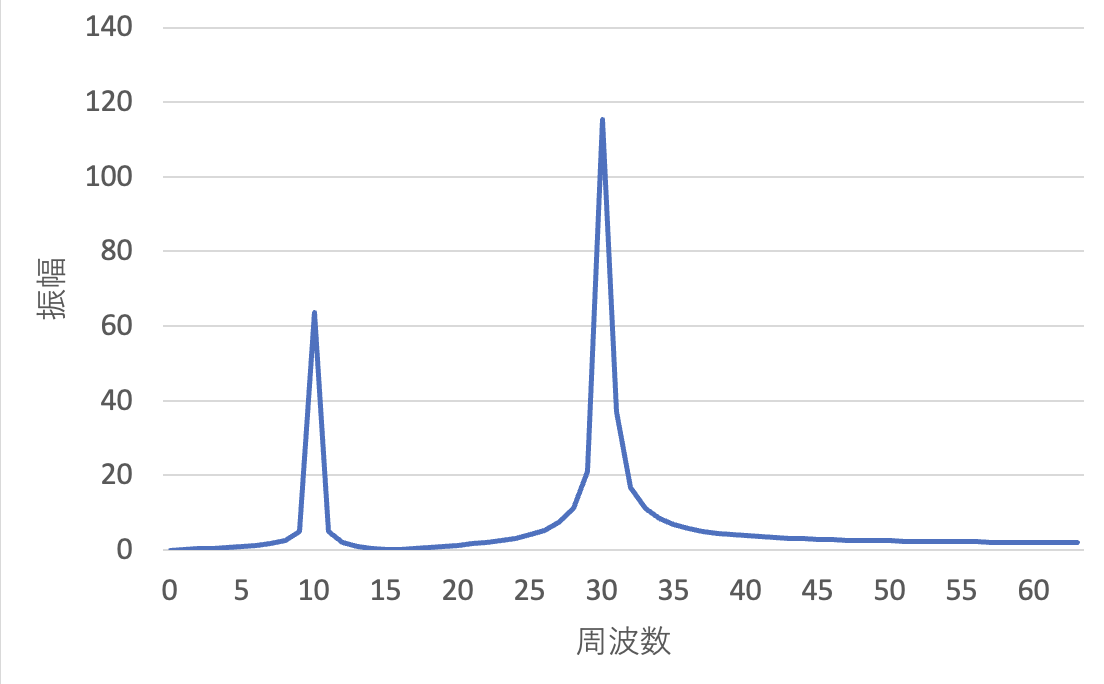
0Hzから63Hzまでを対象に折れ線グラフを描くと次のようになります(複素共役のため$N/2$を対象とする). 10Hzと30Hzの振幅が大きくなっていることが確認できます.
Pythonでフーリエ解析
Pythonを利用してフーリエ解析を試してみましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter15.ipynb とします.
pandas,matplotlib,numpy, SciPyなどのライブラリをインポートしておきましょう.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.io import wavfile
データセットの読込
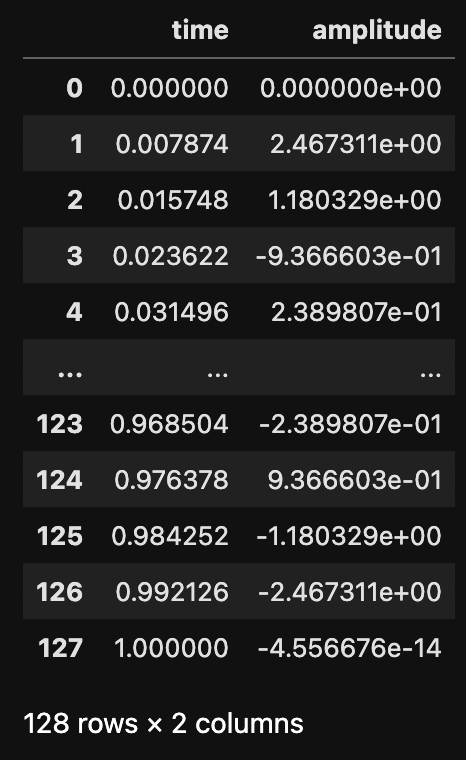
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset14.csv")
display(df)
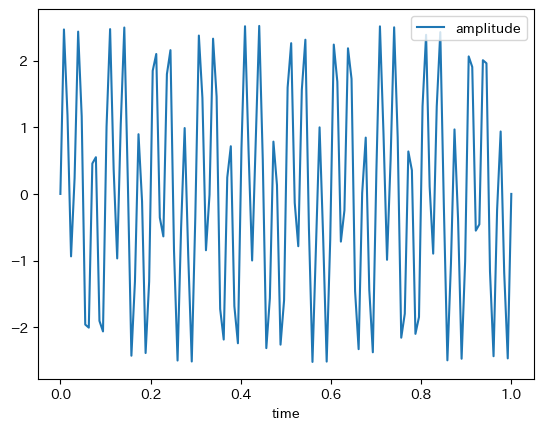
折れ線グラフで可視化してみましょう. 上述の10Hzと30Hzのsin関数を合成したデータであることが確認できます.
df.plot.line(x="time", y="amplitude")
フーリエ変換
np.fft.fftでフーリエ変換を適用します.
フーリエ変換された結果を折れ線グラフで表示します.
Excelの結果と同様に,10Hzと30Hzの振幅が大きくなっていることが確認できます.
fft_data = np.abs(np.fft.fft(df["amplitude"]))
plt.plot(fft_data)
plt.xlim(0, 63)
plt.xlabel("周波数")
plt.ylabel("振幅")
音声ファイルをフーリエ変換
最後にピアノの「ド」の音声ファイル(do.wav)をフーリエ変換してみましょう.
WAVファイルの読み込みにはwavfile.readを利用します.
do = wavfile.read("do.wav") # 261.63Hz
このWAVファイルはステレオになっていますが,
左のチャネル(left_channel)のみを対象とします.
データ数は86,272,サンプリングレートは44,100Hzであることから,
$86272 / 44100 \simeq 1.96$秒の音声データであることがわかります.
rate = do[0]
left_channel = do[1][:,0]
right_channel = do[1][:,1]
size = len(left_channel)
print(size) # データ数
print(rate) # サンプリングレート
print(left_channel[0:10]) # 先頭10個のデータを表示
86272
44100
[-327680 -327680 -196608 -262144 -393216 -196608 -131072 -131072 65536
196608]
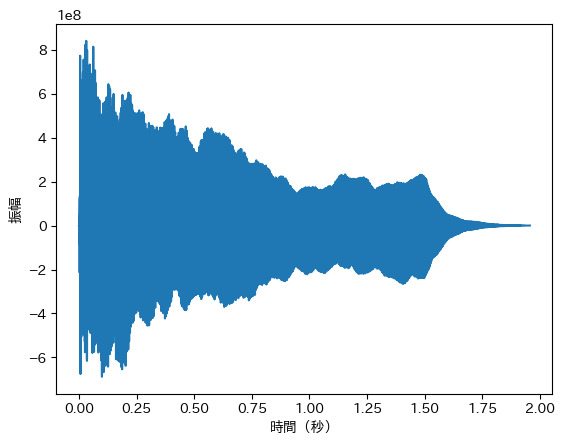
音声データを折れ線グラフで可視化します. 振幅が徐々に減衰する波のデータであることがわかります.
second = np.linspace(0, (size / rate), size) # 横軸
plt.plot(second, left_channel)
plt.xlabel("時間(秒)")
plt.ylabel("振幅")
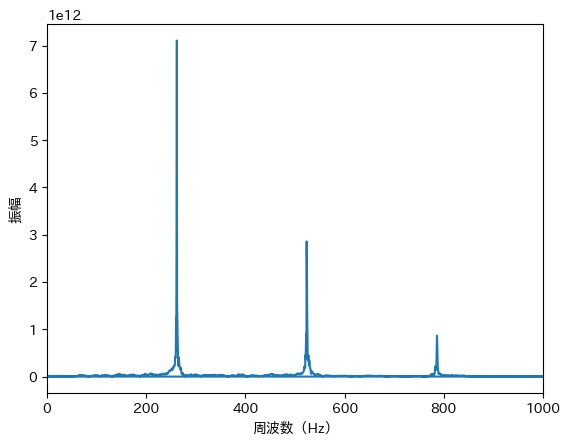
音声データをフーリエ変換します. この結果,261Hz付近に大きな振幅が確認できます. また,その2倍の522Hz,3倍の783Hzにも振幅が表れています. これは 倍音 と呼ばれる現象で,倍音の違いが楽器や歌声の音色を決めると言われます.
fft_data = np.abs(np.fft.fft(left_channel))
fft_freq = np.fft.fftfreq(size, d=1.0/rate)
plt.plot(fft_freq, fft_data)
plt.xlim(0, 1000)
plt.xlabel("周波数(Hz)")
plt.ylabel("振幅")