回帰分析③・ロジスティック回帰
ロジスティック回帰
ロジスティック関数への回帰を利用した分類手法である ロジスティック回帰 を取り上げます. 「回帰」となっていますが,「分類」のためのアルゴリズムであることに注意してください. ここでは,アヤメ(Iris)の分類問題に挑戦します. アヤメは草地に自生している多年草です.
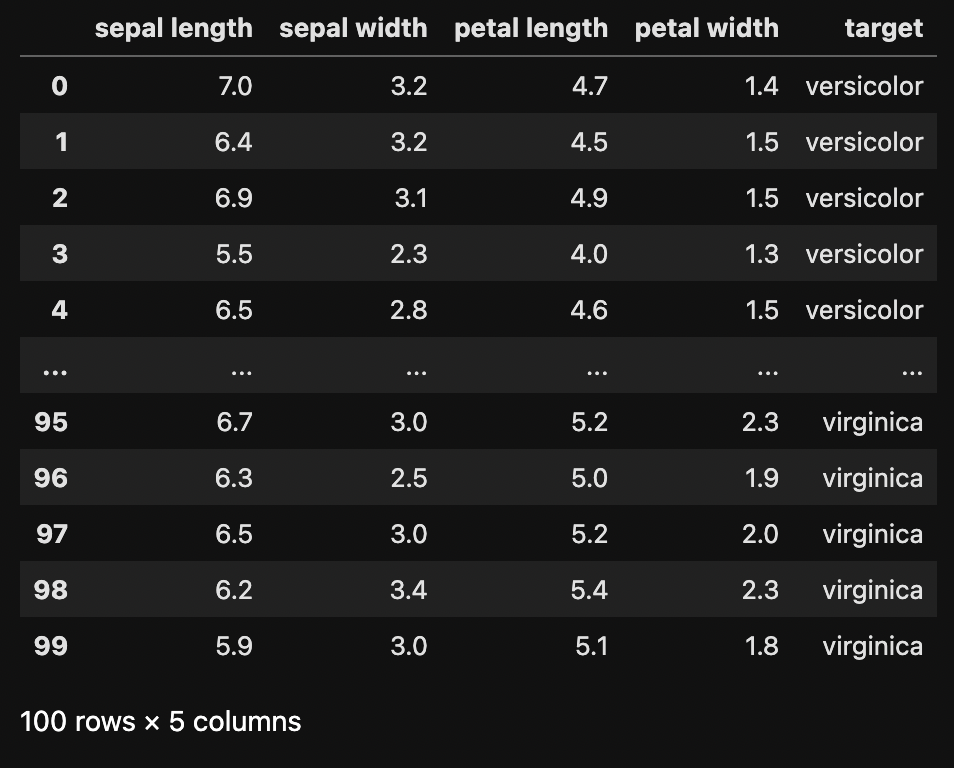
アヤメは種類に応じてがく片と花弁の特徴が異なります. 次の表は Versicolor と Virginica という種類のアヤメのデータです. 各データはがく片の長さ$x_1$,がく片の幅$x_2$,花弁の長さ$x_3$,花弁の幅$x_4$の4つの属性で構成されています. これら4つの変数$x_1, x_2, x_3, x_4$を利用して,アヤメの種類(Versicolor,または,Virginica)を当てることが目的となります.
| がく片の長さ$x_1$ | がく片の幅$x_2$ | 花弁の長さ$x_3$ | 花弁の幅$x_4$ | 種類 |
|---|---|---|---|---|
| 7.0 | 3.2 | 4.7 | 1.4 | versicolor |
| 6.9 | 3.1 | 4.9 | 1.5 | versicolor |
| 6.3 | 3.3 | 6.0 | 2.5 | virginica |
| 5.8 | 2.7 | 5.1 | 1.9 | virginica |
ここでは,がく片の長さ$x_1$とがく片の幅$x_2$の2種類の変数を利用したロジスティック回帰による分類を考えます. まず,係数$W = \left\{ w_0, w_1, w_2 \right\}$と,変数$X = \left\{ 1, x_1, x_2 \right\}$の内積を$g(x)$とします.
$$ g(X) = W \cdot X = w_0 \cdot 1 + w_1 \cdot x_1 + w_2 \cdot x_2 $$
この$g(x)$を用いて ロジスティック関数 は次のように定義されます.
$$ f(X) = \frac{1}{1 + e^{-g(X)}} = \frac{1}{1 + e^{-(w_0 + w_1 \cdot x_1 + w_2 \cdot x_2})} $$
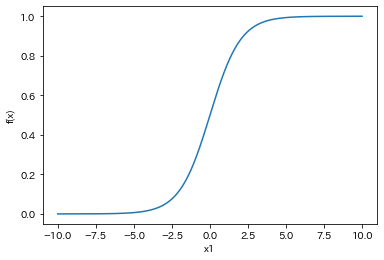
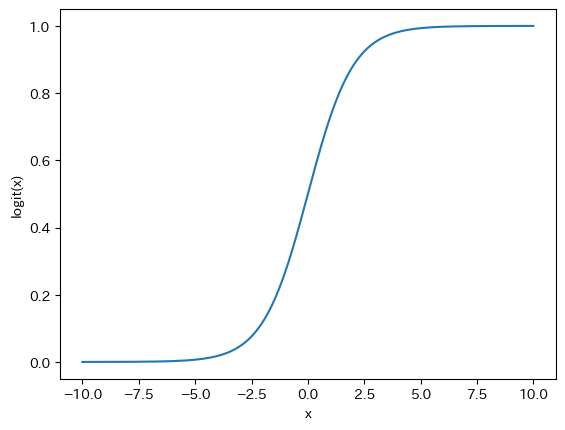
例として,$w_0=0$,$w_1=1$,$w_2=0$のときを考えましょう. このとき,ロジスティック関数$f(x)$は次のように表されます. $x_1$が大きくなると$f(x)$は1に漸近し,$x_1$が小さくなると$f(x)$は0に漸近することがわかります.
$$ f(X) = \frac{1}{1 + e^{-x_1}} $$
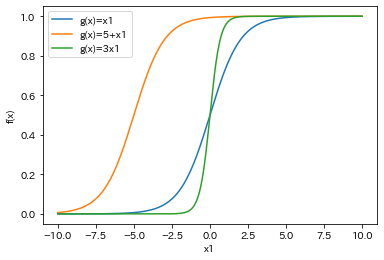
同様に$w_0=5$,$w_1=1$,$w_2=0$と,$w_0=0$,$w_1=3$,$w_2=0$も合わせてプロットしてみます. 係数を変えるとロジスティック関数の傾きの変化や,左右への平行移動が確認できます.
$$ f(X) = \frac{1}{1 + e^{-(5 + x_1)}} $$
$$ f(X) = \frac{1}{1 + e^{-(3 \cdot x_1)}} $$
ロジスティック回帰は2値の分類が基本であり,$f(X)$は一方の値の分類確率を表し,尤度 と呼ばれます.例えば,$f(X)$がvirginicaである尤度(確率)を表すとすると,$1-f(X)$はversicolorである尤度(確率)を表します. この尤度(確率)を観測されたサンプルごとに掛け合わせた 尤度関数(同時確率) $L$ を最大化するような係数$W$を求めることが目的となります. ここで,種類がversinicaのサンプルを$X^{nica}$,versicolorのサンプルと$X^{color}$と表すとすると,$L$は次のように表されます.
$$ L = \prod_{i} f(X_{i}^{nica}) \times \prod_{j} (1 - f(X_{c}^{color})) $$
サンプル数が多い場合,$f(X) \leq 1$であることから,$L$は非常に小さな値になってしまう傾向があります. このため,一般的には$L$の対数を用いた 対数尤度 $log(L)$が用いられます. このとき,$\log(a \times b) = \log(a) + \log(b)$のように,乗算を和算に変換できることも嬉しい点です.
$$ \log(L) = \sum_{i} \log(f(X_{i}^{nica})) + \sum_{j} (1 - \log(f(X_{c}^{color}))) $$
データセット
ここでは,次のCSV形式のデータセットを利用します.
下記のURLからファイルをダウンロードしてください.
アヤメ(Iris)のデータセットであり,がく片の長さ(Sepal Length),がく片の幅(Sepal Width),花弁の長さ(Petal Length),花弁の幅(Petal Width)の4つの属性で構成されます.
ターゲット(target)は,分類目標となる各レコードのカテゴリ(ラベル)であり,versicolorとvirginicaの2種類です.
sepal length,sepal width,petal length,petal width,target
6.4,3.2,4.5,1.5,versicolor
6.9,3.1,4.9,1.5,versicolor
5.5,2.3,4.0,1.3,versicolor
6.5,2.8,4.6,1.5,versicolor
・・省略・・
6.3,3.3,6.0,2.5,virginica
5.8,2.7,5.1,1.9,virginica
7.1,3.0,5.9,2.1,virginica
6.3,2.9,5.6,1.8,virginica
6.5,3.0,5.8,2.2,virginica
・・省略・・
Excelでロジスティック回帰
Excelを利用してロジスティック回帰を試してみましょう. ダウンロードしたファイルをExcelで開いてください, がく片の長さ$x_1$とがく片の幅$x_2$の2つの変数を利用して,アヤメの種類を分類します.
変数
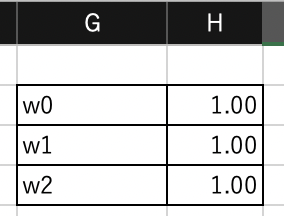
$H3$,$H4$,$H5$に係数$w_0$,$w_1$,$w_2$を入力します. ここでは仮に$w_0=1$,$w_1=1$,$w_2=1$とします.
ロジスティック関数
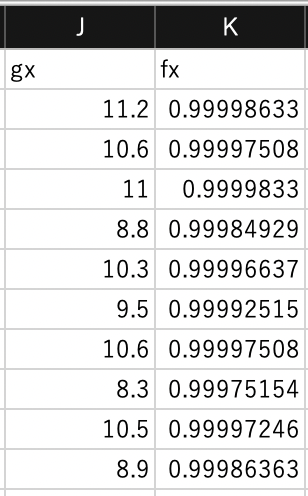
$J$列に内積$g(X)$を計算します. 例えば$J2$には次の式を入力します. 係数の$H3$,$H4$,$H5$は絶対参照となることに注意してください.
=$H$2*1+$H$3*A2+$H$4*B2
$K$列にロジスティック関数$f(X)$を計算します.
例えば$K2$には次の式を入力します.
EXP(x)は$e^{x}$を表す関数です.
=1/(1+EXP(-1*J2))
対数尤度
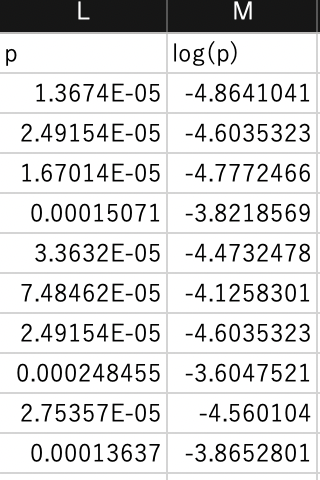
$P$列に尤度を計算します.
例えば,$L2$には次の式を入力します.
IF関数を利用して,種類がversicolorのときは1-K2,virginicaの時はK2を尤度とします.
=IF(E2="versicolor",1-K2,K2)
$Q$列に対数尤度を計算します.
例えば,$Q2$には次の式を入力します.
LOG10(x)関数は$log_{10}(x)$を表す関数です.
=LOG10(L2)
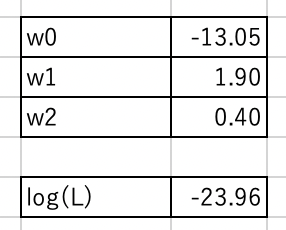
$H6$に対数尤度の和$L$を計算します. 計算結果は$-210.77$になります. この値を最大化することが目的となります.
=SUM(M2:M101)
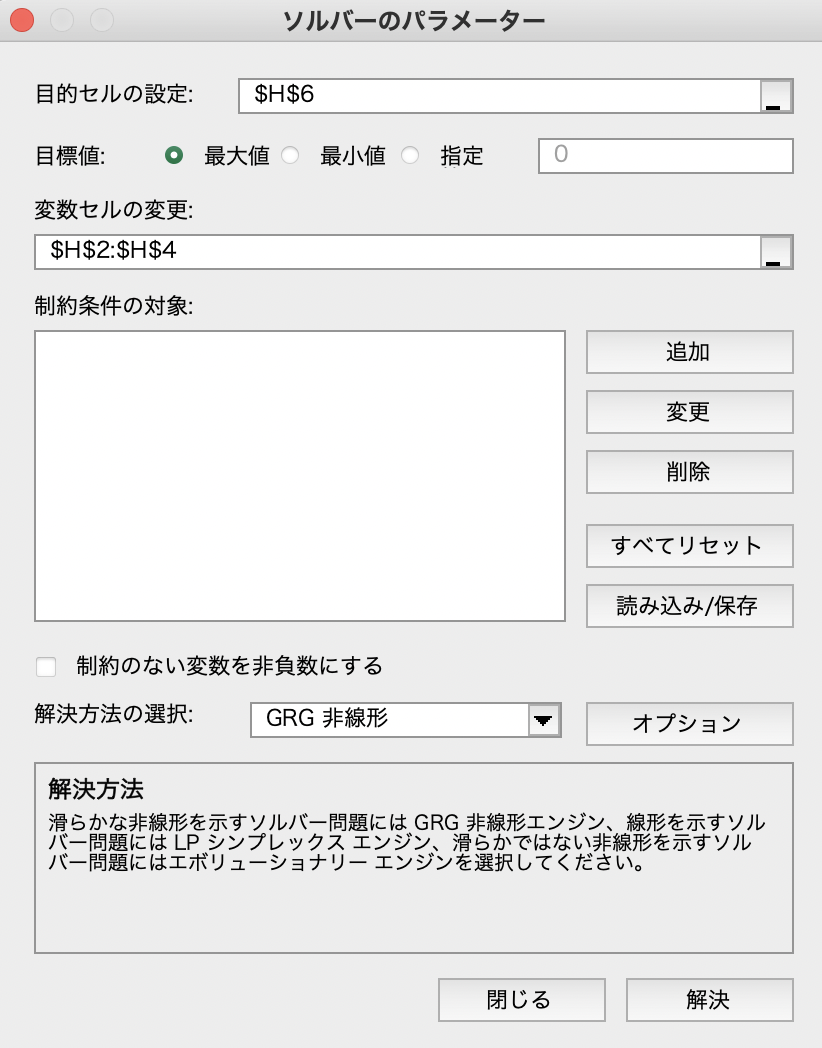
ソルバー
ソルバーを設定します. 目的セルは対数尤度$L$が計算された$H6$です. 変数セルは係数$w_1$,$w_2$,$w_3$が入力された$H2:H4$です. 最後に「制約のない変数を非負数にする」のチェックを外して,「解決」をクリックしてください. この結果,$w_1=-13.05$,$w_2=1.90$,$w_3=0.40$が得られ,対数尤度$L=-23.96$になりました.
正解率
導出された係数を用いて,分類の正解率を算出しましょう.
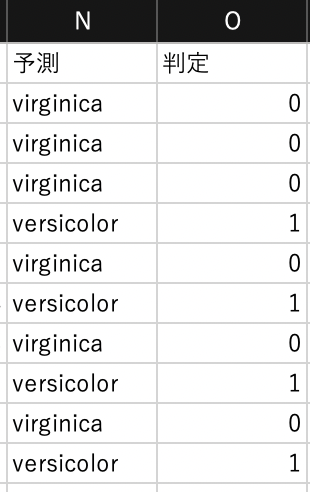
$N$列に分類されたアヤメの種類を計算します.
例えば,$N2$には次の式を入力します.
IF関数を利用して,ロジスティック関数である$K2$が0.5以上ならvirginica,それ以外ならversicolorと判定します.
=IF(K2>=0.5, "virginica","versicolor")
本来のアヤメの種類を表す$E$列と,分類(予測)されたアヤメの種類を表す$N$列が一致しているかどうかを$O$列で表します.
例えば,$O2$には次の式を入力します.
一致するときは1,異なるときは0が設定されます.
=IF(E2=N2,1,0)
$O$列の1が入力されたセルをSUM関数でカウントし,$H8$に入力します.
この結果,$75$件のアヤメの種類が一致したことがわかります.
サンプル数は100件であるため,正解率は$75\%$ということになります(正確には交差検証が必要).
Pythonでロジスティック回帰
Pythonを利用してロジスティック回帰を試してみましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter13.ipynb とします.
pandas,matplotlib,numpy, SciPyなどのライブラリをインポートしておきましょう.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from scipy.optimize import minimize
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset12.csv")
display(df)
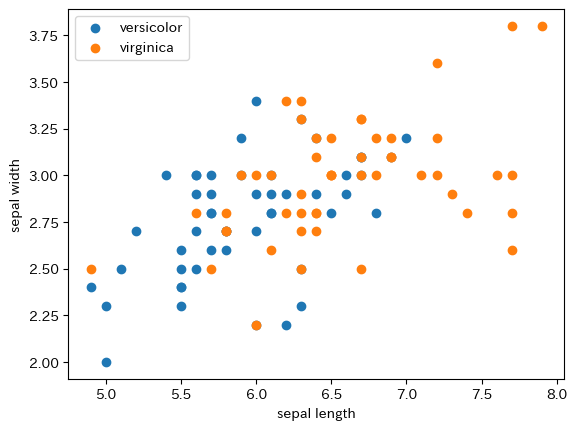
データを散布図で確認してみましょう. 横軸はがく片の長さ(Sepal Length),縦軸はがく片の幅(Sepal Width)を表しています.
df_versicolor = df[df["target"]=="versicolor"]
df_virginica = df[df["target"]=="virginica"]
plt.scatter(df_versicolor["sepal length"], df_versicolor["sepal width"], label="versicolor")
plt.scatter(df_virginica["sepal length"], df_virginica["sepal width"], label="virginica")
plt.legend()
plt.xlabel("sepal length")
plt.ylabel("sepal width")
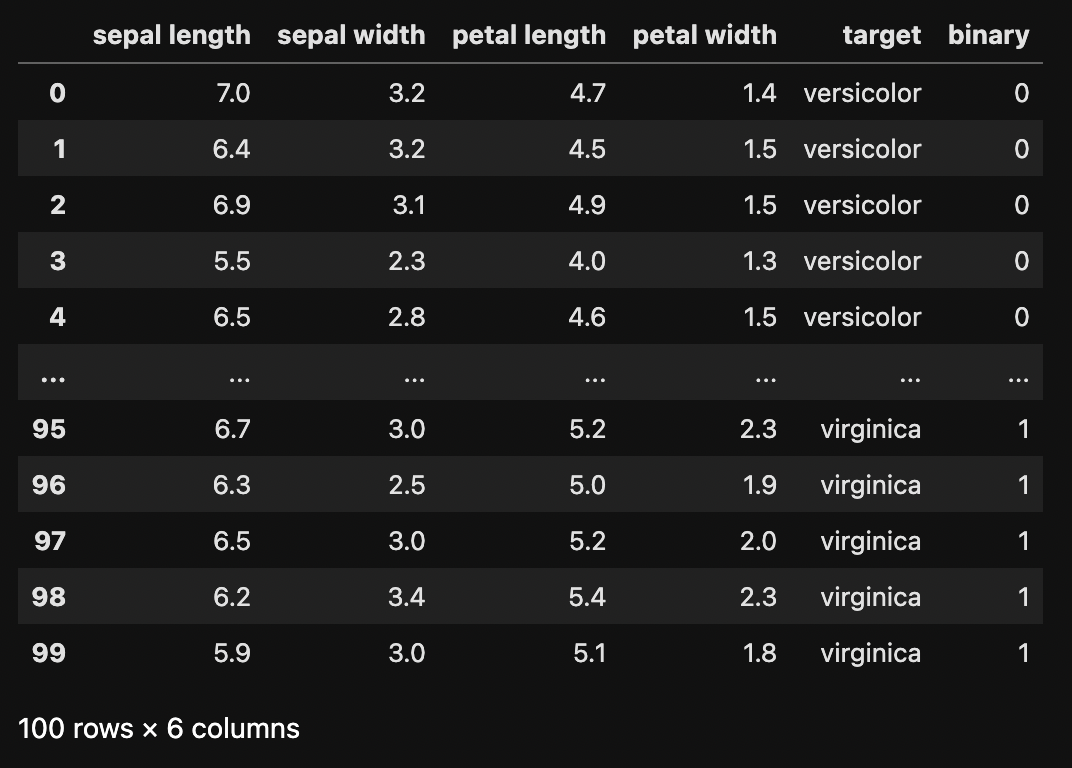
後述で尤度を計算するために,アヤメの種類(target)をバイナリに変換しておきます.
versicolorは0,virginicaは1に変換します.
# ターゲットを0,1に変換
df_target = df[["target"]].replace({"target": {"versicolor": 0, "virginica": 1}})
df = df.assign(binary=df_target)
display(df)
ロジスティック関数
ロジスティック関数を定義します.
# ロジスティック関数
def logit(x):
value = 1 / (1 + np.exp(-x))
return value
ロジスティック関数のグラフを描いてみましょう.
x_ = np.arange(-10, 10, 0.01)
y_ = logit(x_)
plt.plot(x_,y_)
plt.xlabel("x")
plt.ylabel("logit(x)")
係数$W$と変数$X$の内積を,ロジスティック関数の引数とした回帰モデル$f(X)$を定義します.
# ロジスティック関数を利用した回帰モデル
def fx(w, x):
gx = np.sum(w * x, axis=1) # 行方向に加算
y = logit(gx)
return y
変数$X$は,がく片の長さ(Sepal Length)と,がく片の幅(Sepal Wdith)で構成します.
先頭の列に1.0を挿入し,$w_0$と掛け合わせることにします.
最初の要素は$X=(1.0, 7.0, 3.2)$となります.
# x0=1の列を追加
x = df[["sepal length", "sepal width"]].to_numpy()
x = np.insert(x, 0, 1, axis=1)
print(x[0:5])
[[1. 7. 3.2]
[1. 6.4 3.2]
[1. 6.9 3.1]
[1. 5.5 2.3]
[1. 6.5 2.8]]
係数$W=(1, 1, 1)$のときの$f(X)$を算出してみます.
# f(x)の算出
w = np.array([1, 1, 1])
y = fx(w, x)
print(y[0:5])
[0.99998633 0.99997508 0.9999833 0.99984929 0.99996637]
対数尤度
対数尤度を定義します. このとき,対数の底は$10$とします.
引数のtargetには,versicolorのとき0,virginicaのとき1を与えます.
このため,変数$d$は,versicolorのとき,$1 - f(x)$を表します.
$$ d = |0 - (1 - f(x))| = |f(x) - 1| = 1 - f(x) $$
同様に,変数$d$は,virginicaのとき,$f(x)$を表します.
$$ d = |1 - (1 - f(x))| = f(x) $$
# 対数尤度
def likelifood(w, x, target):
d = np.abs(target - (1 - fx(w, x)))
d = np.log10(d)
return np.sum(d)
係数$W=(1, 1, 1)$のときの対数尤度$L$を算出してみます.
# 対数尤度の算出
w = np.array([1, 1, 1])
target = df["binary"].to_list()
likelifood(w, x, target)
-210.76562306473724
最適な係数$W$の算出
minimize関数を利用して,対数尤度$L$を最大化するような$W$を求めます.
minimize関数は最小化しかできないため,対数尤度に$-1$を掛けた関数$lx$を定義することで最大化します.
def lx(w, x, target):
return -1 * likelifood(w, x, target)
最適化手法にはネルダー・ミード法を採用します.
w = np.array([1, 1, 1])
result = minimize(lx, w, args=(x, target), method="Nelder-Mead")
print(result.x) # 係数W
print(result.fun) # 対数尤度
この結果,$w_0=-13.05$,$w_1=1.90$,$w_2=0.40$となり,Excelの算出結果と一致していることがわかります. また,最大化された対数尤度は$-23.96$(符号が逆転する)であり,これもExcelの算出結果と一致しています.
[-13.04600867 1.90237087 0.40466111]
23.95692311546384
正解率
分類の正解率を確認しましょう. 正解数をカウントすると$75$となりました. サンプル数は100件であることから,正解率は$75\%$となり,この結果もExcelと一致します.
# 正解率の算出
y = fx(result.x, x)
y = np.array(list(map(lambda x : 0 if x<=0.5 else 1, y))) #0と1に変換
target = np.array(target)
count = np.sum(y == target)
print(count)
75
補足
Pythonのscikit-learnを利用すると簡単にロジスティック回帰を実行できます.
from sklearn.linear_model import LogisticRegression
X = df[["sepal length", "sepal width"]]
Y = df["target"]
lr = LogisticRegression()
lr.fit(X, Y)
この結果,$w_0=-11.11$,$w_1=1.59$,$w_2=0.41$となりました. 上述の結果と一致はしませんが,よく似た値が算出されています. また,正解率も同じ$75\%$であることから,同程度の精度のモデルと考えることができます.
print(lr.coef_) # w1, w2
print(lr.intercept_) # w0
print(lr.score(X, Y)) # 正解率
[[1.5890194 0.40894657]]
[-11.10589861]
0.75
課題
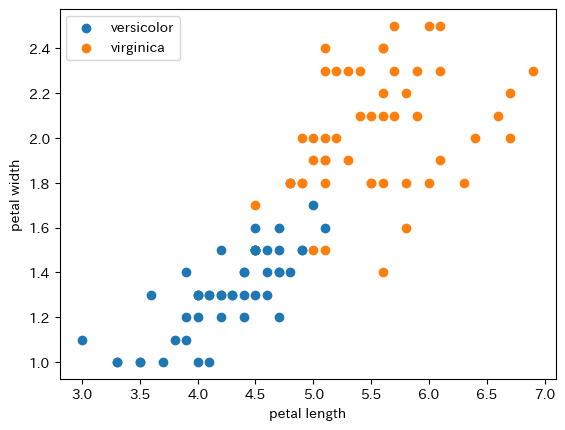
花弁の長さ(Petal Length)$x_3$と,花弁の幅(Petal Width)$x_4$を利用して,アヤメの種類を分類してください.
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter13.ipynb としてください.