回帰分析②・重回帰
重回帰分析と決定係数
説明変数が複数の変数$x_1, x_2, \cdots, x_m$で構成される 重回帰分析 に着目します. 重回帰分析の回帰モデルは次の式で表されます. ここで,$W = \left\{ w_0, w_1, \cdots, w_m \right\}$は回帰モデルの係数です. また,$x_0=1$とみなすことで,説明変数は$X = \left\{ 1, x_1, \cdots, x_m \right\}$のように表すことができます. この結果,回帰係数は$W$と$X$の内積で表されます.
$$ f(X) = W \cdot X = \sum_{i=0}^{m}w_ix_i = w_0 \cdot 1 + w_1 \cdot x_1 + \cdots + w_m \cdot x_m $$
例えば,変数$x_1$を身長,変数$x_2$を座高,変数$y$を体重とした回帰分析を考えます. 次の表はe-Statで公開されている5歳から14歳までの男性の身長,座高,体重の平均です(分かりやすさのため,ここでは多重共線性を考慮しない).
| 年齢 | 身長$x_1$ | 座高$x_2$ | 体重$y$ |
|---|---|---|---|
| 5 | 110.7 | 61.9 | 19.0 |
| 6 | 116.7 | 64.9 | 21.5 |
| 7 | 122.6 | 67.7 | 24.1 |
| 8 | 128.3 | 70.3 | 27.2 |
| 9 | 133.6 | 72.7 | 30.6 |
| 10 | 138.9 | 75.0 | 34.2 |
| 11 | 145.1 | 77.6 | 38.4 |
| 12 | 152.5 | 81.3 | 44.2 |
| 13 | 159.7 | 84.9 | 49.1 |
| 14 | 165.2 | 88.1 | 54.3 |
上記のデータを基に導出した回帰モデルは次の式で表されます. $w_0=-75.47$,$w_1=-0.30$,$w_2=2.03$に対応します.
$$ y = -75.47 + -0.30 \times x_1 + 2.03 \times x_2 $$
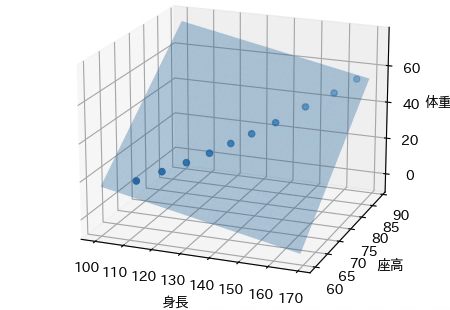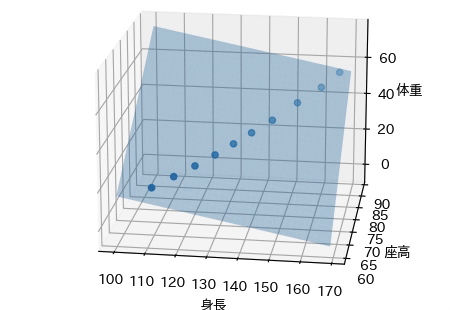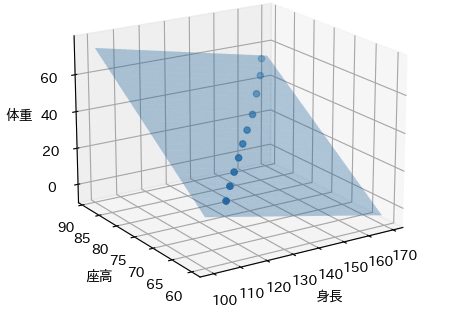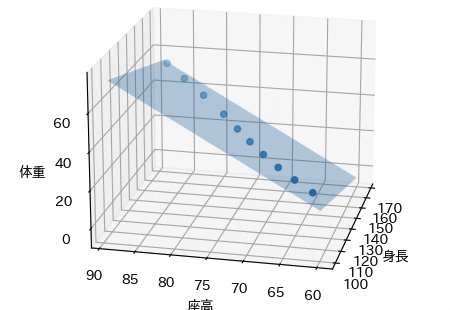
この回帰モデルをグラフで表すと,次の平面で表されます. この平面は,身長・座高と体重との関係を適切に表現できているように思われます.
回帰モデルの適切な係数を導出するには,単回帰と同様に最小二乗法を利用します. 観測された変数$y$と,回帰モデルで算出された値$f(x)$との残差平方和を最小化します.
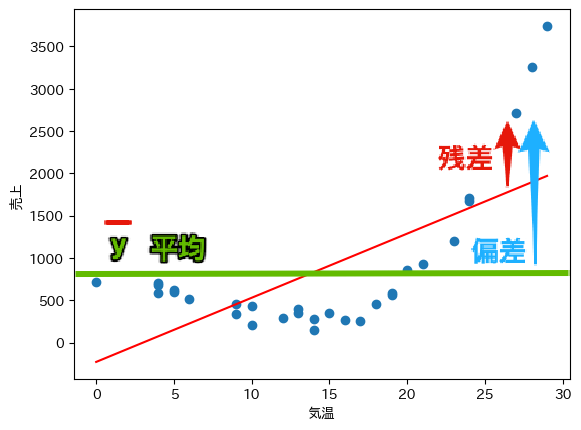
ここでは,算出された回帰モデルの当てはまりの良さを表す 決定係数 $R^2$ について確認しましょう. 決定係数$R^2$は次の式で算出することができます. 分子は残差平方和,分母は偏差平方和($\bar{y}$は$y$の平均値)を表し,$R^2$が1に近ければ相対的に残差が小さいことを示します. 下図に示すように,決定係数は$f(x)=\bar{y}$で表される回帰直線の誤差(偏差)と, $f(x)=w_0+w_1x$で表される回帰直線の誤差(残差)の割合を表す指標と言えます. 最小二乗法は残差平方和を最小化する手法であるため,式中の分子を0に近付ける操作に等しくなります.
$$ R^2 = 1 - \frac{残差平方和}{偏差平方和} = 1 - \sum_{i=0}^{n-1}\frac{(y_i - f(x_i))^2}{(y_i - \bar{y})^2} $$
しかし,重回帰分析においては,説明変数が増えるほど,決定係数$R^2$が大きくなる傾向があります. このため,標本の大きさを$n$,説明変数の数を$m$とするとき,次に示す 自由度調整済みの決定係数 が用いられます.
$$ R^2 = 1 - \sum_{i=0}^{n-1}\frac{(y_i - f(x_i))^2 / (n - m - 1)}{(y_i - \bar{y})^2 / (n-1)} $$
データセット
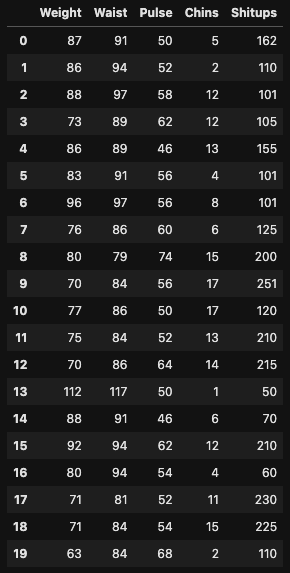
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 運動能力のデータセットであり,体重(Weight[kg]),胴囲(Waist[cm]),心拍(Pulse),懸垂回数(Chins),腹筋回数(Situps)で構成されます.
Weight,Waist,Pulse,Chins,Situps
87,91,50,5,162
86,94,52,2,110
88,97,58,12,101
73,89,62,12,105
86,89,46,13,155
83,91,56,4,101
96,97,56,8,101
76,86,60,6,125
80,79,74,15,200
70,84,56,17,251
77,86,50,17,120
75,84,52,13,210
70,86,64,14,215
112,117,50,1,50
88,91,46,6,70
92,94,62,12,210
80,94,54,4,60
71,81,52,11,230
71,84,54,15,225
63,84,68,2,110
Excelで重回帰分析
Excelの分析ツールを利用して重回帰分析を試してみましょう. ダウンロードしたファイルをExcelで開いてください. 説明変数として,体重$x_1$,胴囲$x_2$,心拍$x_3$,目的変数(被説明変数)として懸垂回数$y$を用います. 回帰モデルは次の式を採用します.
$$ f(x) = w_0 \times 1 + w_1 \times x_1 + w_2 \times x_2 + w_3 \times x_3 $$
分析ツール
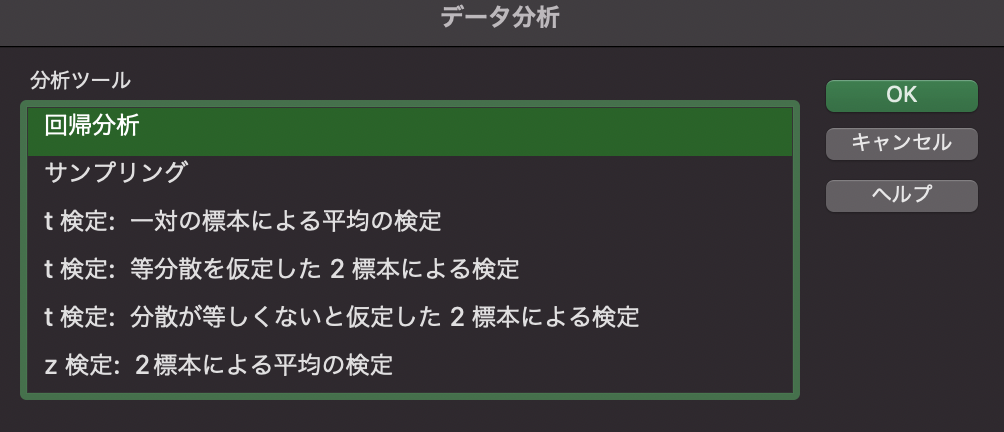
分析ツールから「回帰分析」を選びましょう.
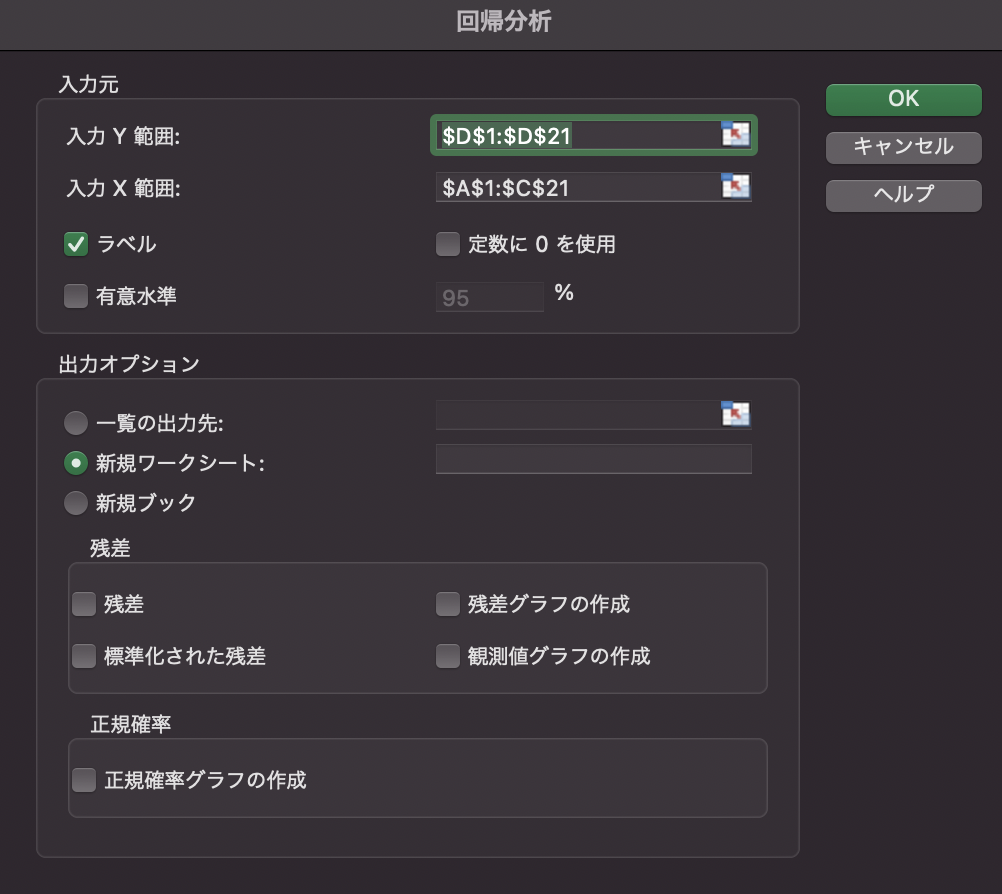
「入力Y範囲」に$D1:D21$,「入力X範囲」に$A1:C21$を入力します. このとき,「先頭行をラベルとして使用」にチェックを入れます.
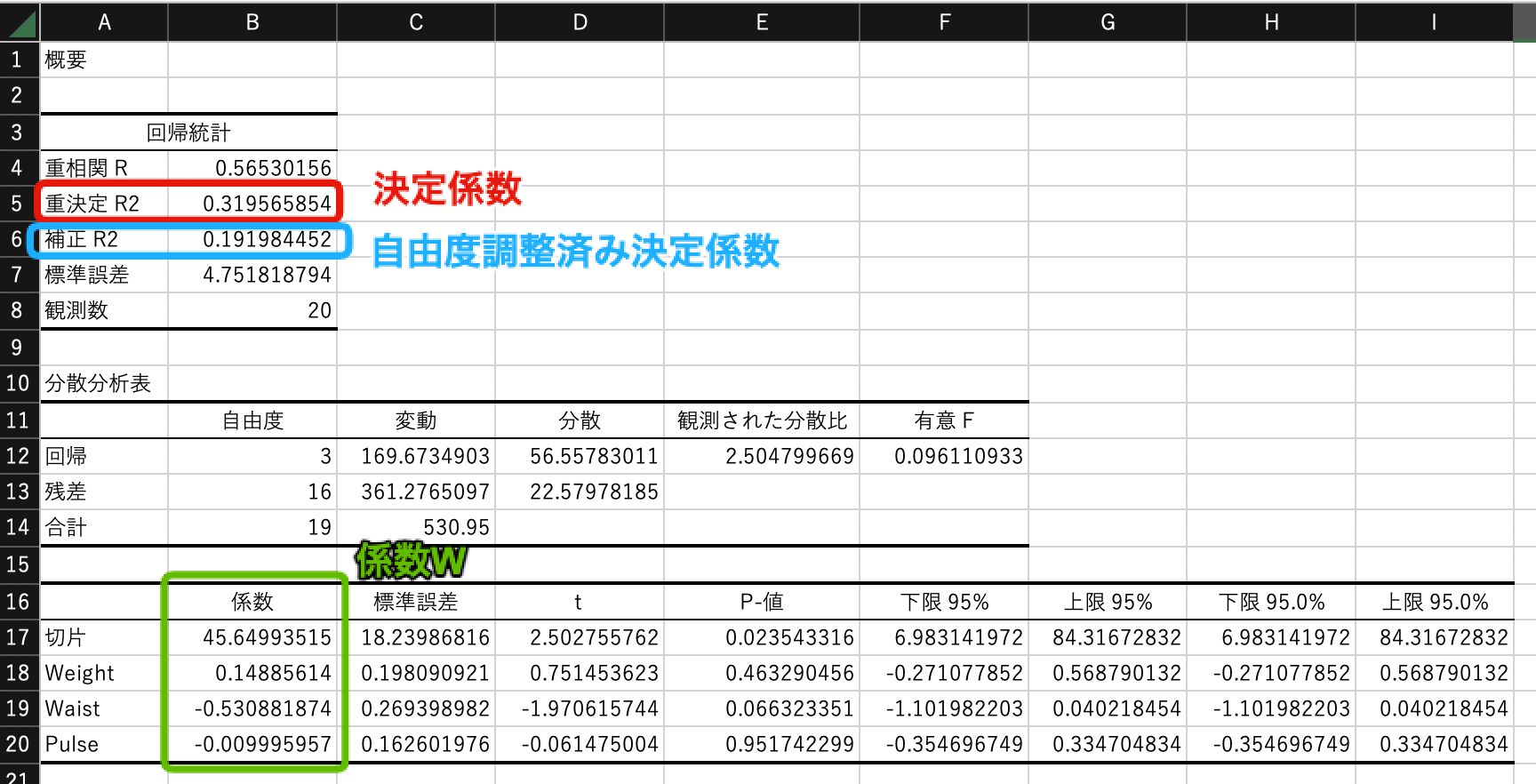
次のような結果が算出されます. 回帰モデルの係数は$w_0=45.65$,$w_1=0.15$,$w_2=-0.53$,$w_3=-0.01$となったことがわかります. また,決定係数$R^2$は0.32,自由度調整済み決定係数$R^2$は0.19となりました. 一般に$R^2 \geq 0.5$のときに当てはまりが良いとみなすため, この回帰モデルの精度は高くないと言えます.
Pythonで重回帰分析
Pythonを利用して重回帰分析を試してみましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter12.ipynb とします.
pandas,matplotlib,numpy, SciPyなどのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import japanize_matplotlib
import numpy as np
from scipy.optimize import minimize
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset11.csv")
display(df)
回帰モデル(重回帰)
重回帰のモデルを利用します.
$$ f(X) = w_0 \cdot 1 + w_1 \cdot x_1 + w_2 \cdot x_2 + w_3 \cdot x_3 $$
回帰式$f(x)$を次のように定義します. 引数の$w$は回帰式の係数を表しています.
# 回帰モデル
def fx(w, x):
y = np.sum(w * x, axis=1) # 行方向に加算
return y
データフレームから体重$x_1$,胴囲$x_2$,心拍$x_3$を抽出し,$x_0=1$を追加した配列を生成します.
# x0=1の列を追加
x = df[["Weight", "Waist", "Pulse"]].to_numpy()
x = np.insert(x, 0, 1, axis=1)
print(x)
[[ 1 87 91 50]
[ 1 86 94 52]
[ 1 88 97 58]
[ 1 73 89 62]
[ 1 86 89 46]
[ 1 83 91 56]
[ 1 96 97 56]
[ 1 76 86 60]
[ 1 80 79 74]
[ 1 70 84 56]
[ 1 77 86 50]
[ 1 75 84 52]
[ 1 70 86 64]
[ 1 112 117 50]
[ 1 88 91 46]
[ 1 92 94 62]
[ 1 80 94 54]
[ 1 71 81 52]
[ 1 71 84 54]
[ 1 63 84 68]]
$w_0=1$,$w_2=2$,$w_2=3$,$w_3=4$として,$f(x)$を計算してみます. 例えば,$x_1=87$,$x_2=91$,$x_3=50$のとき,$f(x)=648$になります.
w = np.array([1, 2, 3, 4])
fx(w, x)
array([648, 663, 700, 662, 624, 664, 708, 651, 694, 617, 613, 611, 655,
776, 634, 715, 659, 594, 611, 651])
残差平方和$E$を次のように定義します.
# 残差平方和(RSS: Residual Sum of Squares)
def rss(w, x, y):
r = (y - fx(w, x))**2
return r.sum()
$w_0=1$,$w_2=2$,$w_2=3$,$w_3=4$として,残差平方和$E$を計算すると,$E=8440451$になります.
w = np.array([1, 2, 3, 4])
rss(w, x, df["Chins"])
8440451
minimize関数を利用して,残差平方和$E$を最小化するような$w$を求めます.
この結果,$w_0=45.65$,$w_1=0.15$,$w_2=-0.53$,$w_3=-0.01$となり,Excelの算出結果と一致しています.
w = np.array([1, 2, 3, 4])
result = minimize(rss, w, args=(x, df["Chins"]), method="Powell")
print(result.x)
[ 4.56500030e+01 1.48856400e-01 -5.30882565e-01 -9.99515930e-03]
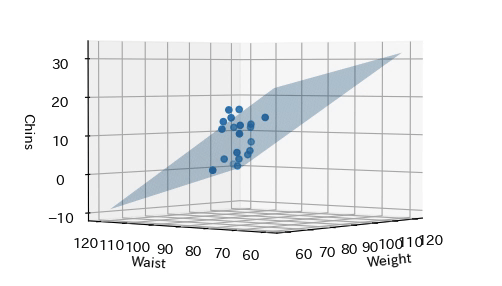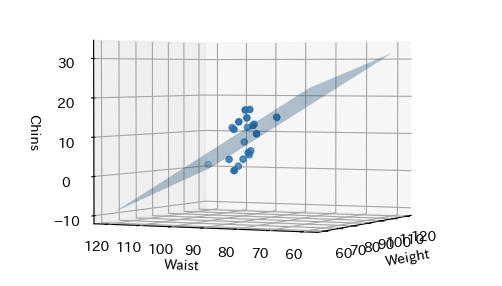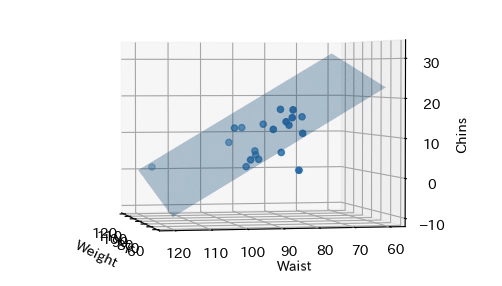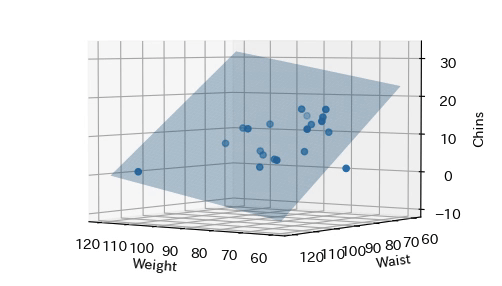
回帰モデル$f(x)$を3次元グラフで可視化します. X軸は体重(Weight),Y軸は胴囲(Waist),Z軸は$f(x)$を表します. 心拍(Pulse)の係数$w_3$は非常に小さな値であり,回帰に寄与していないことから, 可視化対象のデータから除いていることに注意してください. 全体の傾向を平面で表していることが分かります.
# X=Weight Y=Waist Z=Chinsで3次元グラフ(Pulseは用いない)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(df["Weight"], df["Waist"], df["Chins"])
x = np.arange(60, 120, 0.1) # Weight
y = np.arange(60, 120, 0.1) # Waist
X, Y = np.meshgrid(x, y)
Z = []
for j in y:
column = []
for i in x:
array = np.array([1, i, j, 0])
z = fx(result.x, [array])
column.append(z[0])
Z.append(column)
Z = np.array(Z) # 回帰モデル f(x)
ax.plot_surface(X, Y, Z, alpha=0.3)
ax.view_init(-140, 60) # カメラの仰角と方位角
ax.set_xlabel("Weight")
ax.set_ylabel("Waist")
ax.set_zlabel("Chins")
補足
Pythonのscikit-learnを利用すると簡単に重回帰分析を実行できます. 算出された係数と決定係数がExcelの結果と一致していることが分かります.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
X = df[["Weight", "Waist", "Pulse"]].values
Y = df[["Chins"]].values
lr.fit(X, Y)
print(lr.coef_) # 係数 w1 w2 w3
print(lr.intercept_) # 係数 w0
print(lr.score(X, Y)) # 決定係数 R^2
[[ 0.14885614 -0.53088187 -0.00999596]]
[45.64993515]
0.3195658543022284
自由度調整済み決定係数は次のように計算します. この結果もExcelの結果と一致しています.
yss_list = [] # 実測値と平均値の差の2乗
rss_list = [] # 残差の2乗
Z = lr.predict(X)
for y, z in zip(Y, Z):
yss = (y - np.mean(Y))**2
rss = (y - z)**2
yss_list.append(yss)
rss_list.append(rss)
# 決定係数
print(1 - (np.sum(rss_list) / np.sum(yss_list)))
# 自由度調整済み決定係数
N = len(df)
k = 3
print(1 - ((np.sum(rss_list) / (N - k - 1)) / (np.sum(yss_list) / (N - 1))))
0.3195658543022284
0.19198445198389635
課題
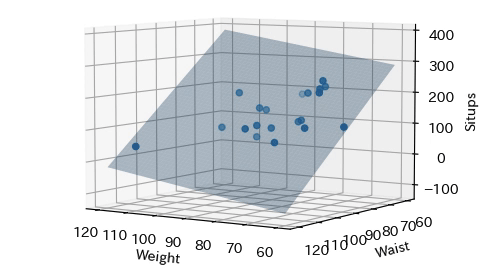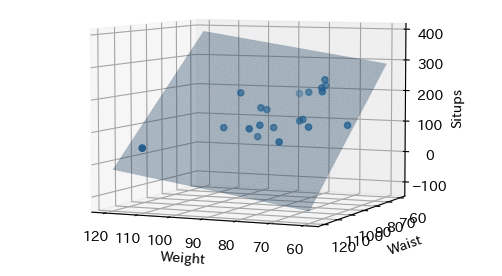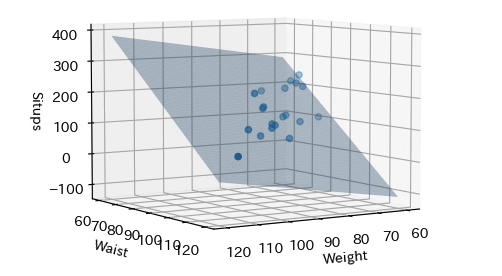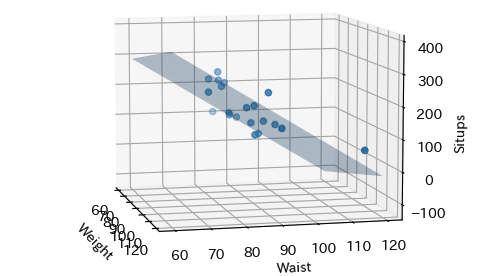
説明変数として,体重$x_1$,胴囲$x_2$,心拍$x_3$,目的変数(被説明変数)として腹筋回数$y$として重回帰分析しなさい.
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter12.ipynb としてください.