回帰分析①・単回帰
回帰分析
回帰 とは,連続値の変数$y$を,変数$x$を用いたモデル(関数)で表現することを意味します. このとき,変数$x$を 説明変数 ,変数$y$を 目的変数(被説明変数) と呼び, 説明変数と目的関数の関係性を明らかにすることが回帰分析の目的となります. 回帰分析には 単回帰分析 と 重回帰分析 の2種類があります. 単回帰分析は説明変数$x$が1つの変数で表される場合です. 一方,重回帰分析は説明変数$x$が複数の変数で構成される場合です. 今回は単回帰分析に着目します.
$$ y = f(x) $$
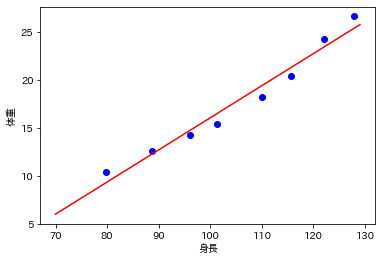
説明変数と目的変数のデータに基づいて, 適切な回帰モデルを導出することで,事象の傾向を把握し,未来を予測することが可能となります. 例えば,変数$x$を身長,変数$y$を体重とした回帰分析を考えます. 次の表はe-Statで公開されている1歳から8歳までの男性の身長と体重の平均です.
| 年齢 | 身長$x$ | 体重$y$ |
|---|---|---|
| 1 | 79.7 | 10.4 |
| 2 | 88.6 | 12.6 |
| 3 | 96.0 | 14.2 |
| 4 | 101.2 | 15.4 |
| 5 | 110.0 | 18.2 |
| 6 | 115.6 | 20.4 |
| 7 | 122.0 | 24.2 |
| 8 | 127.8 | 26.6 |
上記のデータを基に導出した1次式の回帰モデルは次の式で表されます. この1次式で表される直線は,身長と体重の関係を適切に表現できているように思われます.
$$ y = 0.33 \times x - 17.44 $$
では,上記の回帰モデルを導出するにはどうすれば良いでしょうか. ここでは, 最小二乗法 を採用してみましょう. 最小二乗法では,観測された変数$y$と,回帰モデルで算出された値$f(x)$との残差(誤差)の2乗を最小化することで, 回帰モデルの適切な係数を導出する手法です. 1次式の回帰モデルを次のように定義します. ここで,$w_0$と$w_1$が回帰モデルの係数であり,$w_1$が傾き,$w_0$が切片を表します.
$$ f(x) = w_1 \times x + w_0 $$
このとき,残差の2乗は 残差平方和$E$ と呼ばれ,次の式で計算できます. この残差平方和を最小化するような$w_0$と$w_1$を求めれば良いということになります.
$$ E = \sum_{i=0}^{n-1}(y_i - f(x_i))^2 = \sum_{i=0}^{n-1}(y_i - (w_1 \cdot x_i + w_0))^2 $$
データセット
ここでは,次のCSV形式のデータセットを利用します. 下記のURLからファイルをダウンロードしてください. 気温$x$とアイスクリームの売上$y$のデータです.
気温,売上
24,1706
23,1195
29,3741
14,146
4,698
9,459
24,1671
5,616
4,588
15,353
(省略)
Excelで単回帰分析
Excelのソルバーを利用して,アイスクリームの売上$y$と気温$x$の関係を回帰分析しましょう. ダウンロードしたファイルをExcelで開いてください. 回帰モデルは次の1次式を採用します.
$$ f(x) = w_1 \times x + w_0 $$
変数
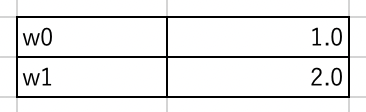
$G3$と$G4$に変数$w_0$と$w_1$を入力します. 初期状態では,$w_0=1$と$w_1=2$に設定しましょう.
回帰モデル
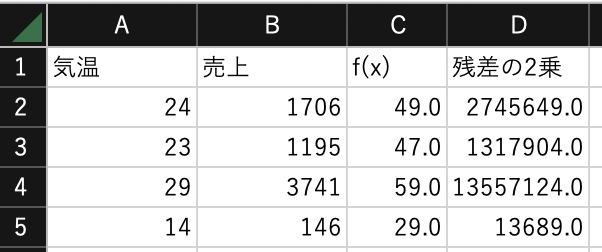
C列に回帰モデル$f(x)$を計算しましょう. 例えば$C2$には次の式を入力します. このとき,$G2$と$G3$は絶対参照にします.
$$ =$G$2+$G$3*A2 $$
残差の2乗
D列に残差の2乗$(y-f(x))^2$を計算しましょう. 例えば,$D2$には次の式を入力します.
$$ =(B2-C2)^2 $$
目的関数
$G5$に目的関数となる残差平方和を計算します. この値を最小化することが目的となります. 初期状態の残差平方和は43,615,578です.
$$ =SUM(D2:D31) $$
ソルバー
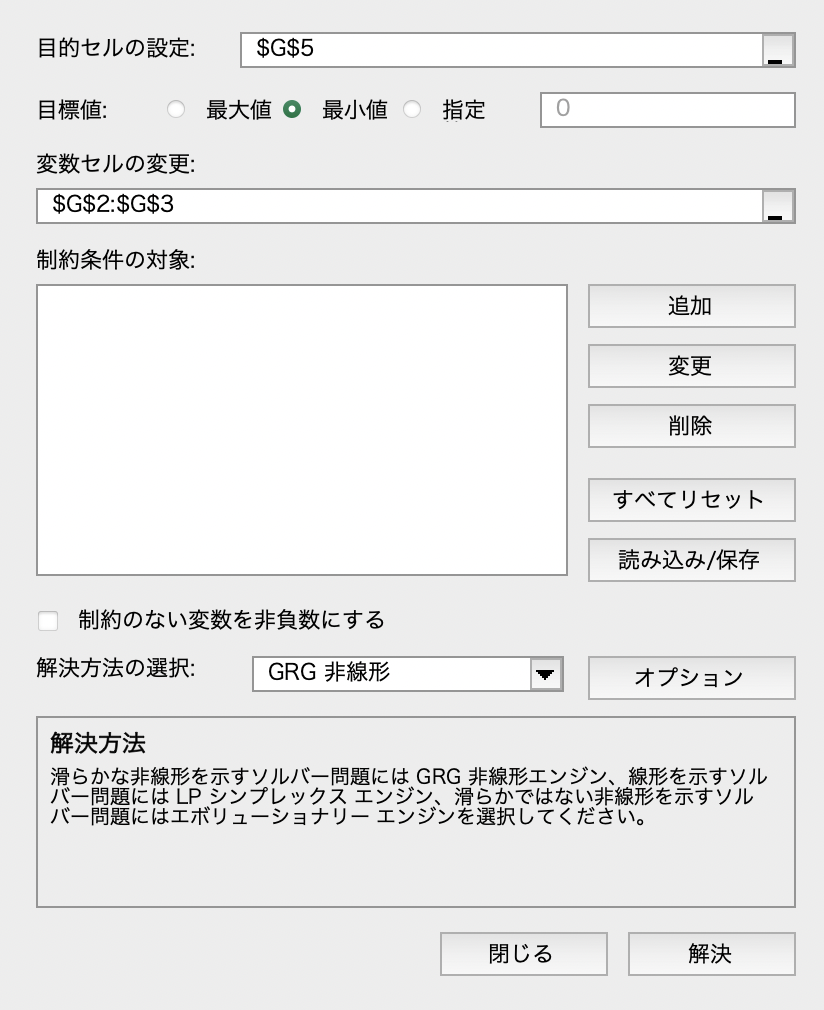
データ・タブからソルバーを選択します. ソルバーのパラメータに,目的セル(目的関数),変数セル(変数)を設定します. 解決方法はGRG非線形を選択します.
最後に解決ボタンをクリックすると,次の結果が導出されます. $w_0=-229.2$,$w_1=75.8$となり,残差平方和は12,799,069です.
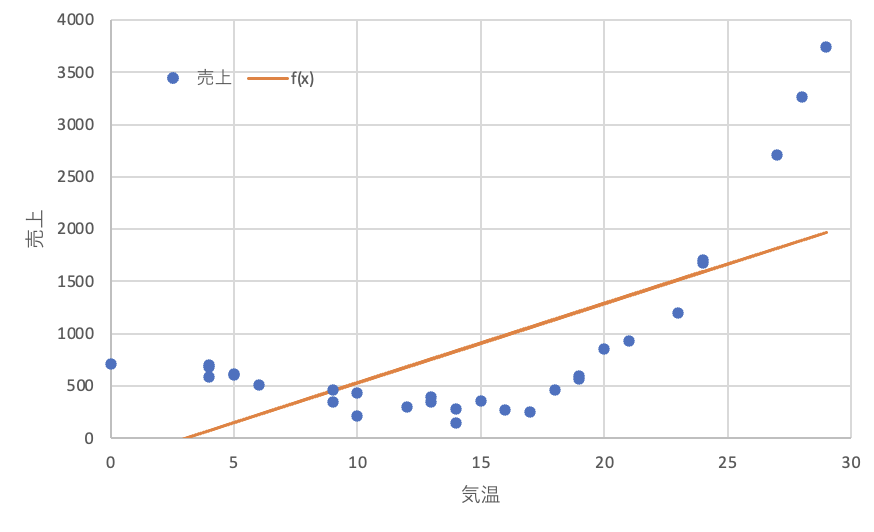
グラフの作成
売上と回帰モデル$f(x)$を折れ線グラフにしましょう. このとき,$f(x)$の方はマーカーではなく線で表示することにします. 算出された回帰モデルは,おおまかに全体の傾向を近似していることがわかります. 後述のPythonでは,直線を表す1次式ではなく,2次式,3次式を用いることで,より誤差の小さな回帰モデルを導出します.
Pythonで単回帰分析
Pythonを利用して,アイスクリームの売上$y$と気温$x$の関係を回帰分析しましょう.
Jupyter Labを起動して,Python 3のノートブックを開きます.
ノートブックの名前は chapter11.ipynb とします.
pandas,matplotlib,numpy, SciPyなどのライブラリをインポートしておきましょう.
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
from scipy.optimize import minimize
データセットの読込
read_csv関数でデータセットを読み込みます.
df = pd.read_csv("dataset10.csv")
display(df)
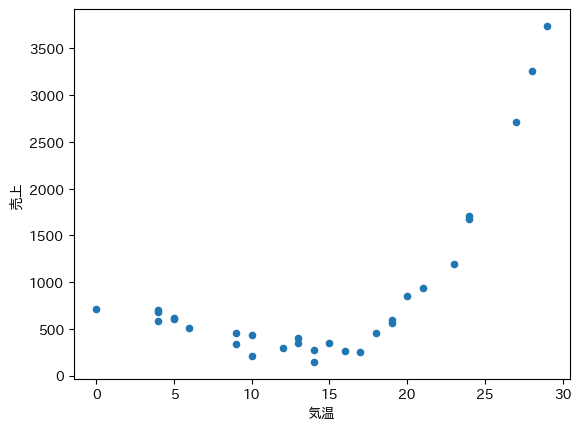
データを散布図で確認してみましょう.
df.plot.scatter(x="気温", y="売上")
回帰モデル(1次式)
1次式の回帰モデルを利用します.
$$ f(x) = w_1 \times x + w_0 $$
回帰式$f(x)$を次のように定義します. 引数の$w$は回帰式の係数を表しています.
# 回帰式(1次式)
def fx(w, x):
y = w[0] + w[1] * x
return y
$w_0=1$,$w_1=2$として,$f(x)$を計算してみます. 例えば,$x=24$のとき,$f(x)=49$になります.
w = np.array([1, 2])
fx(w, df["気温"])
0 49
1 47
2 59
3 29
4 9
...省略...
残差平方和$E$を次のように定義します.
# 残差平方和(RSS: Residual Sum of Squares)
def rss(w, x, y):
r = (y - fx(w, x))**2
return r.sum()
$w_0=1$,$w_1=2$として,残差平方和$E$を計算すると,$E=43615578$になります. この値はExcelで計算した値と一致しています.
w = np.array([1, 2])
rss(w, df["気温"], df["売上"])
43615578
minimize関数を利用して,残差平方和$E$を最小化するような$w$を求めます.
この結果,$w_0=-229.2$,$w_1=75.8$となり,Excelの算出結果と一致しています.
w = np.array([1, 2])
result = minimize(rss, w, args=(df["気温"], df["売上"]), method="Powell")
print(result.x)
[-229.17387211 75.79448188]
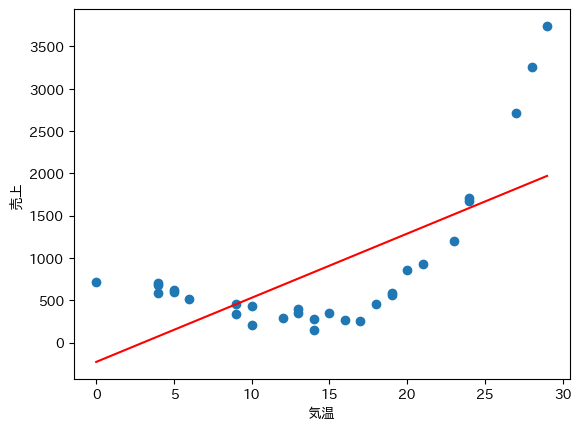
回帰モデル$f(x)$を折れ線グラフで可視化します. 全体の傾向を直線で表していることが分かります.
x = np.arange(0, 30)
plt.plot(x, fx(result.x, x), c="red")
plt.scatter(df["気温"], df["売上"])
plt.xlabel("気温")
plt.ylabel("売上")
回帰モデル(2次式)
2次式の回帰モデルを利用します.
$$ f(x) = w_2 \times x^2 + w_1 \times x + w_0 $$
回帰式$f(x)$を次のように定義します.
# 回帰式(2次式)
def fx(w, x):
y = w[0] + w[1] * x + w[2] * x**2
return y
$w_0=1$,$w_1=2$,$w_2=3$として,$f(x)$を計算してみます. 例えば,$x=24$のとき,$f(x)=1777$になります.
w = np.array([1, 2, 3])
fx(w, df["気温"])
0 1777
1 1634
2 2582
3 617
4 57
...省略...
minimize関数を利用して,残差平方和$E$を最小化するような$w$を求めます.
この結果,$w_0=1334.5$,$w_1=-216.5$,$w_2=9.8$となりました.
w = np.array([1, 2, 3])
result = minimize(rss, w, args=(df["気温"], df["売上"]), method="Powell")
print(result.x)
[1334.514003 -216.53725371 9.8457794 ]
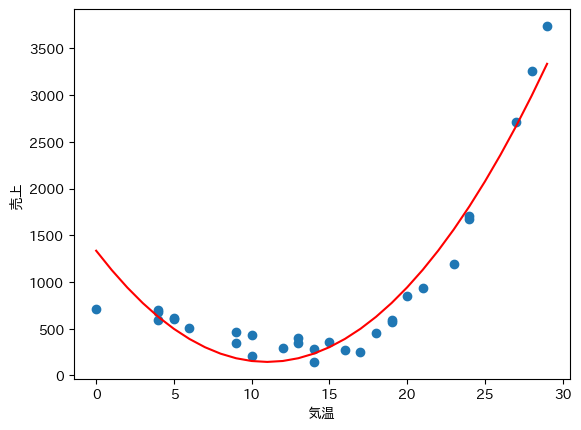
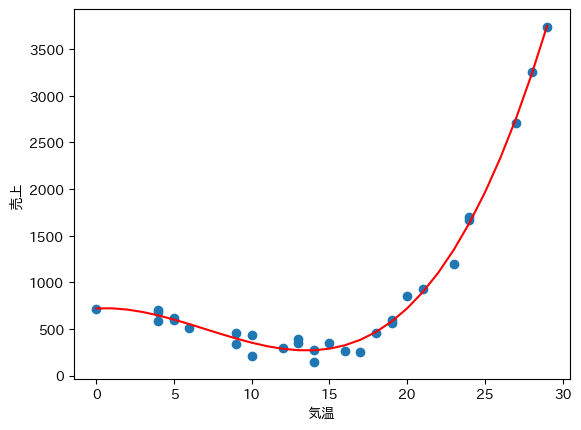
回帰モデル$f(x)$を折れ線グラフで可視化します. 1次式よりも2次式の方が表現力が向上するため, より全体の傾向を表した曲線が得られていることが分かります.
x = np.arange(0, 30)
plt.plot(x, fx(result.x, x), c="red")
plt.scatter(df["気温"], df["売上"])
plt.xlabel("気温")
plt.ylabel("売上")
課題
3次式の回帰モデルを利用して回帰分析しなさい.
$$ f(x) = w_3 \times x^3 + w_2 \times x^2 + w_1 \times x + w_0 $$
Jupyter Labで作成したノートブックを保存し,ダウンロードして提出してください. ノートブックをダウンロードするには,メニューから Download を選択します. ノートブックのファイル名は chapter11.ipynb としてください.