線形計画法③・巡回セールスマン問題

巡回セールスマン問題

計算量が多くNP困難な問題として知られる 巡回セールスマン問題 に挑戦しましょう． 前回の最短経路問題と同様に，線形計画問題の一つとして扱うことが可能です．

例題

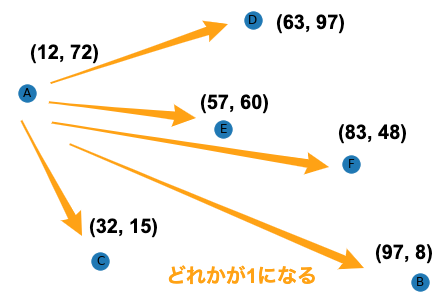
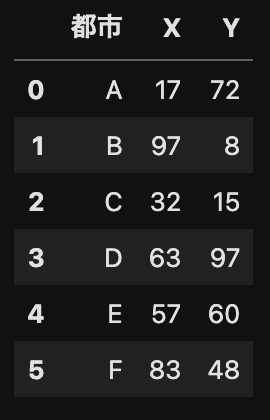
次の図に示されるようにAからFまでの6つの都市が点在している． 各都市の位置（座標）は$(X, Y)$で表されている． このとき，Aからスタートし，全ての都市を一度ずつ訪れてから， Aに戻ってくる経路のうち，最短の経路を求めよ．

Image from Gyazo

まずは，6つの都市を巡る経路が幾つあるか数えてみましょう． 最初の都市はAで確定しているため，2番目に訪れる都市は5通りです． 同様に3番目に訪れる都市は4通りです． よって，都市数$n$における候補となる経路数は次の式で与えられます．

$$ (n-1)! = 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 $$

このとき，$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A$と， 訪れる順番を逆さまにした$A \rightarrow F \rightarrow E \rightarrow D \rightarrow C \rightarrow B \rightarrow A$は同じ距離になるため，実質的な候補となる経路は上記の半分となります．

$$ \frac{(n-1)!}{2} = \frac{5!}{2} = \frac{5 \times 4 \times 3 \times 2 \times 1}{2} = \frac{120}{2} = 60 $$

この経路数は，階乗のオーダーで急激に大きくなってしまうため，$n$が大きくなると有限時間で解を得ることが困難になることが知られています（組合わせ爆発）． 日本科学未来館の動画「『フカシギの数え方』おねえさんといっしょ！みんなで数えてみよう」が面白いので時間があれば視聴してみましょう．

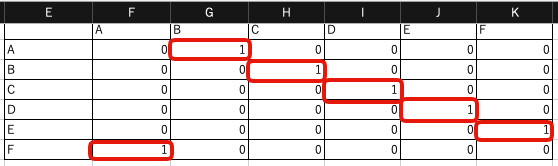
問題を定式化するために，変数$x_{ij}$を導入します． ノード$i$からノード$j$の経路を含むときは$x_{ij}=1$，経路を含まないときは$x_{ij}=0$とします． 例えば，経路$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A$は， 次の行列$x_{ij}$で表すことができます．

i ＼ j A B C D E F
A $x_{AA}=0$ $x_{AB}=1$ $x_{AC}=0$ $x_{AD}=0$ $x_{AE}=0$ $x_{AF}=0$
B $x_{BA}=0$ $x_{BB}=0$ $x_{BC}=1$ $x_{BD}=0$ $x_{BE}=0$ $x_{BF}=0$
C $x_{CA}=0$ $x_{CB}=0$ $x_{CC}=0$ $x_{CD}=1$ $x_{CE}=0$ $x_{CF}=0$
D $x_{DA}=0$ $x_{DB}=0$ $x_{DC}=0$ $x_{DD}=0$ $x_{DE}=1$ $x_{DF}=0$
E $x_{EA}=0$ $x_{EB}=0$ $x_{EC}=0$ $x_{ED}=0$ $x_{EE}=0$ $x_{EF}=1$
F $x_{FA}=1$ $x_{FB}=0$ $x_{FC}=0$ $x_{FD}=0$ $x_{FE}=0$ $x_{FF}=0$

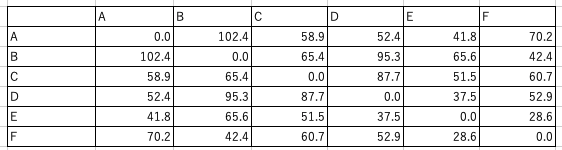
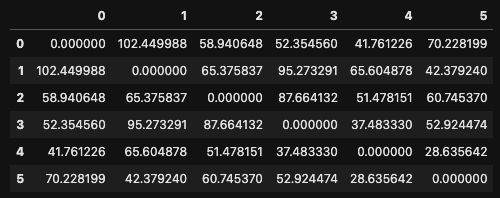
同様にノード$i$からノード$j$までの距離（コスト）を行列$w_{ij}$で表します． 2ノード間の距離はノードの座標から算出します． $w_{AA}$など同じノードの距離は$0$になります．

i ＼ j A B C D E F
A $w_{AA}=0$ $w_{AB}=102$ $w_{AC}=58$ $w_{AD}=52$ $w_{AE}=41$ $w_{AF}=70$
B $w_{BA}=102$ $w_{BB}=0$ $w_{BC}=65$ $w_{BD}=95$ $w_{BE}=65$ $w_{BF}=42$
C $w_{CA}=58$ $w_{CB}=65$ $w_{CC}=0$ $w_{CD}=87$ $w_{CE}=51$ $w_{CF}=60$
D $w_{DA}=52$ $w_{DB}=95$ $w_{DC}=87$ $w_{DD}=0$ $w_{DE}=37$ $w_{DF}=52$
E $w_{EA}=41$ $w_{EB}=65$ $w_{EC}=51$ $w_{ED}=37$ $w_{EE}=0$ $w_{EF}=28$
F $w_{FA}=70$ $w_{FB}=42$ $w_{FC}=60$ $w_{FD}=52$ $w_{FE}=28$ $w_{FF}=0$

上記の$x_{ij}$と$w_{ij}$を用いて目的関数である経路長は次のように定義できます． この目的関数を最小化することを狙います．

$$ 経路長 = \sum_{i, j \in E} w_{ij} \cdot x_{ij} $$

例えば，経路$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A$の経路長は次のように計算できます（$x_{ij}=0$の項は省略）．

$$ 経路長 = 1 \times 102 + 1 \times 65 + 1 \times 87 + 1 \times 37 + 1 \times 28 + 1 \times 70 = 389 $$

次に制約条件を定義します． 制約条件は，出発条件，到着条件，ループの禁止 の3種類に分類されます（部分経路を回避するには，後述の MTZ制約(Miller-Tucker-Zemlin Formulation) が必要）．

出発条件は次の式で表されます． ここで，$\forall i$は任意のノード$i$を表します． 例えば，ノード$A$から出発とすると，その次には$B,C,D,E,F$のいずれかに遷移します． このため，$x_{AA}+x_{AB}+x_{AC}+x_{AD}+x_{AE}+x_{EF}$は常に1となります．

$$ \sum_{j} x_{ij} = 1, \forall i $$

Image from Gyazo

到着条件は次の式で表されます． ここで，$\forall j$は任意のノード$j$を表します． 例えば，ノード$A$に到着すると，その前には$B,C,D,E,F$のいずれかに滞在してるはずです． このため，$x_{AA}+x_{BA}+x_{CA}+x_{DA}+x_{EA}+x_{FA}$は常に1となります．

$$ \sum_{i} x_{ij} = 1, \forall j $$

Image from Gyazo

ループの禁止は次の式で表されます． 例えば，ノード$A$から，同じノード$A$に遷移することはあり得ません． このため，$x_{AA}$は常に0です．

$$ x_{ii} = 0, \forall i $$

上記の目的関数と制約条件を利用して，巡回セールスマン問題を解いてみましょう．

データセット

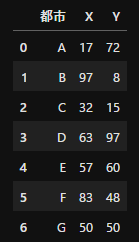
ここでは，次のCSV形式のデータセットを利用します． 下記のURLからファイルをダウンロードしてください． 上述と同じ巡回セールスマン問題であり，各都市の座標を表しています．

dataset9.csv

都市,X,Y
A,17,72
B,97,8
C,32,15
D,63,97
E,57,60
F,83,48

Excelで巡回セールスマン問題

Excelのソルバーを利用して巡回セールスマン問題を解きましょう． ダウンロードしたファイルをExcelで開いてください．

変数

$E1:K7$に変数$x_{ij}$を入力します． 初期状態では，経路$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A$を表すために，$x_{AB}=1$，$x_{BC}=1$，$x_{CD}=1$，$x_{DE}=1$，$x_{EF}=1$，$x_{FA}=1$に設定しましょう．

Image from Gyazo

距離行列

$E9:K15$に距離行列$w_{ij}$を入力します． ノード間のコストはユークリッド距離で計算します． 例えば，ノード$A$とノード$B$の距離を求める$G10$には次の式を入力します．

$$ =SQRT(($B$3-$B2)^2+($C$3-$C2)^2) $$

Image from Gyazo

目的関数

$F17$に，SUMPRODUCT関数を利用して，目的関数を入力します． 初期状態の経路$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow A$の距離は$391.8$であることが分かります．

$$ =SUMPRODUCT(F2:K7,F10:K15) $$

Image from Gyazo

制約条件

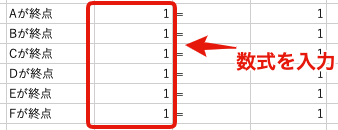
$E19:H24$に出発条件を入力します． 例えば，Aから出発する条件を入力する$F19$には次の式を入力します．

$$ =SUM(F2:K2) $$

Image from Gyazo

$E26:H31$にの到着条件を入力します． 例えば，Aに到着する条件を入力する$F26$には次の式を入力します．

$$ =SUM(F2:F7) $$

Image from Gyazo

$E33:H38$にループの禁止の制約条件を入力します． 例えば，AからAに戻るループを禁止する条件を入力する$F33$には次の式を入力します．

$$ =F2 $$

Image from Gyazo

ソルバー

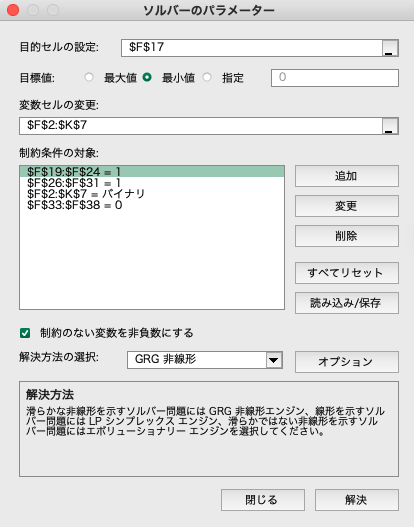
データ・タブからソルバーを選択します． ソルバーのパラメータに，目的セル（目的関数），変数セル（変数），制約条件の対象（制約条件）を設定します． このとき，$x_{ij}$は，0と1の2値であるため， 制約条件としてバイナリ（bin）を設定しておきます． また，解決方法はGRG非線形を選択します．

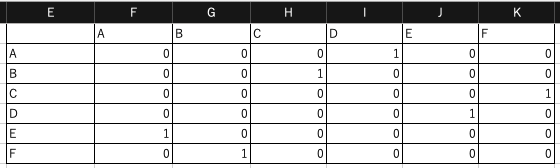
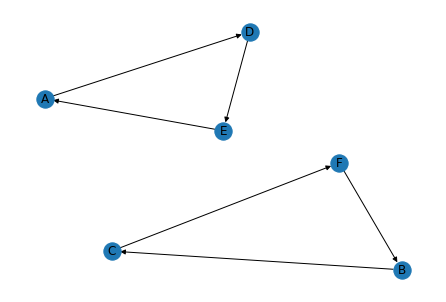
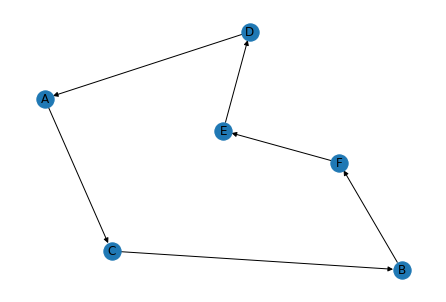
Image from Gyazo

最後に解決ボタンをクリックすると，次の結果が導出されます． この結果は，$A \rightarrow D \rightarrow E \rightarrow A$と，$B \rightarrow C \rightarrow F \rightarrow B$の2つの部分経路を表しており，巡回セールスマン問題の解として条件を満たしていません． この部分経路を回避するには，MTZ制約 を導入する必要があります．

Image from Gyazo

Image from Gyazo

Pythonで巡回セールスマン問題

Pythonを利用して巡回セールスマン問題を解きましょう． ここでは MTZ制約 を導入して部分経路の生成を回避します． Jupyter Labを起動して，Python 3のノートブックを開きます． ノートブックの名前は chapter10.ipynb とします． pandas，matplotlib，numpy，PuLPなどのライブラリをインポートしておきましょう． ユークリッド距離を計算するscipy.spatial，ネットワークを可視化するnetworkxもインポートします．

import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
import numpy as np
from pulp import *
from scipy.spatial import distance
import networkx as nx

データセットの読込

read_csv関数でデータセットを読み込みます．

df = pd.read_csv("dataset9.csv")
display(df)

Image from Gyazo

グラフの描画

6都市の位置関係をグラフで表示します．

# グラフの作成
graph = nx.DiGraph()

# ノードのラベル
node_list = ["A", "B", "C", "D", "E", "F"]
graph.add_nodes_from(node_list)
	
# ノードの座標
pos_list = {}
for i, row in df.iterrows():
    city, x, y = row
    pos_list[city] = (x, y)
       
# グラフの描画
nx.draw(graph, pos=pos_list, with_labels=True)

Image from Gyazo

距離行列

距離行列$w_{ij}$を定義します． distance.euclidian((x1, y1), (x2, y2))関数で，2点間のユークリッド距離を算出します．

# 距離行列
w = np.zeros((len(df), len(df)))

for i,row1 in df.iterrows():
    for j, row2 in df.iterrows():
        city1, x1, y1 = row1[0], row1[1], row1[2]
        city2, x2, y2 = row2[0], row2[1], row2[2]
        dist = distance.euclidean((x1, y1), (x2, y2))
        w[i][j] = dist

Image from Gyazo

変数

PuLPを利用して変数$x_{ij}$を隣接行列として定義します． データのカテゴリとしてcat=binaryを指定します．

# 変数（隣接行列）
x = []

for i in range(len(df)):
    tmp = []
    for j in range(len(df)):
        tmp.append(LpVariable(f"x_{i}{j}", cat="Binary"))
    x.append(tmp)
	
print(x)

[[x_00, x_01, x_02, x_03, x_04, x_05], [x_10, x_11, x_12, x_13, x_14, x_15], [x_20, x_21, x_22, x_23, x_24, x_25], [x_30, x_31, x_32, x_33, x_34, x_35], [x_40, x_41, x_42, x_43, x_44, x_45], [x_50, x_51, x_52, x_53, x_54, x_55]]

後述するMTZ制約のために，ノードを訪問する順番を表す変数$u_{i}$を定義します． データのカテゴリとしてcat=Integerを指定します． また，対象の問題が6都市であることから，最小値は0，最大値は5に設定します．

# 変数（ノードを訪問する順番）
u = []

for i in range(len(df)):
    u.append(LpVariable(f"u_{i}", cat="Integer", lowBound=0, upBound=len(df)-1))
	
print(u)

[u_0, u_1, u_2, u_3, u_4, u_5]

問題

巡回セールスマン問題を定義します． ここで，LpMinimizeを指定し，目的関数を最小化することを指定します．

# 問題
problem = LpProblem("巡回セールスマン問題", LpMinimize)

目的関数

目的関数を定義します．

# 目的関数
cost = 0

for i in range(len(df)):
    for j in range(len(df)):
        cost += w[i][j] * x[i][j]

problem += cost

制約条件

出発条件を定義します． 隣接行列の行方向の加算を1に制約します．

# 制約条件（出発条件）
for i in range(len(df)):
    sum = 0
    for j in range(len(df)):
        sum += x[i][j]
        
    problem += sum == 1, f"{i}から出発"

終点の条件を定義します． 隣接行列の列方向の加算を1に制約します．

# 制約条件（到着条件）
for j in range(len(df)):
    sum = 0
    for i in range(len(df)):
        sum += x[i][j]
        
    problem += sum == 1, f"{j}に到着"

ループの禁止の条件を定義します． 同じノードに留まることを禁止します．

# 制約条件（ループの禁止）
for i in range(len(df)):
    problem += x[i][i] == 0, f"{i}に留まることを禁止"

部分経路を禁止するためのMTZ制約を定義します． MTZ制約は次の式で表されます． $M$は任意の大きな整数ですが，ここでは都市数の5を設定します．

$$ u_i - u_j \leq M \times (1 - x_{ij}) - 1 $$

MTZ制約の意味を考えてみます． 例えば$A \rightarrow B$に遷移するときは，$x_{AB}$は1になります． このとき，Aはスタート地点であるため，Aの訪問順番を表す$u_A$は0です．

$$ u_A - u_B \leq 5 \times (1 - x_{AB}) - 1 $$

これを$u_B$について解くと，$u_B \geq 1$となり，Bの訪問順番は1以上に制約されます．

$$ u_B \geq 1 $$

次に$B \rightarrow C$に遷移するときは，$x_{BC}$は1になります． このとき，Bの訪問順番を表す$u_B$は1以上に制約されています． ここで，Bの訪問順番が2番目だとすると$u_B=1$であり，Cの訪問順番は2以上に制約されます．

$$ u_B - u_C \leq 5 \times (1 - x_{BC}) - 1 $$

$$ u_C \geq 2 $$

これを繰り返すと，経路の訪問順番に従って$u_i$は決定されることになり，部分経路の生成を回避することができます． ただし，スタート地点であるAはゴール地点でもあることから，最後に2度目の訪問を認めるため，MTZ制約の対象からは除きます．

# 制約条件（部分経路を禁止）
for i in range(len(df)):
    for j in range(len(df)):
        if i != j and j != 0:
            problem += u[i] - u[j] <= len(df) * (1 - x[i][j]) - 1, f"{i}の次に{j}に到達"

# A（0）をスタート地点に設定
problem += u[0] == 0, "0をスタート地点に設定"

問題の確認

定義した問題を確認してみましょう． 目的関数，制約条件，変数の条件などを確認することができます．

print(problem)

解決

solve()関数で問題を解きます． この関数の戻り値が1(Optimal)のときは，最適解が得られたことを表します．

status = problem.solve()
print(LpStatus[status])

Optimal

導出された最適解を確認しましょう． $A \rightarrow C \rightarrow B \rightarrow F \rightarrow E \rightarrow D$が最短経路として導出されたことが分かります． また，この経路の距離（コスト）が285.17であることも確認できます．

# 最適化された変数の確認
for i in range(len(df)):
    for j in range(len(df)):
        value = x[i][j].varValue
        print(f"x[{i}][{j}]={value}")
        
for i in range(len(df)):
    value = u[i].varValue
    print(f"u[{i}]={value}")
    
# 距離
print(problem.objective.value())

x[0][0]=0.0
x[0][1]=0.0
x[0][2]=1.0
x[0][3]=0.0
x[0][4]=0.0
x[0][5]=0.0
x[1][0]=0.0
x[1][1]=0.0
x[1][2]=0.0
x[1][3]=0.0
x[1][4]=0.0
x[1][5]=1.0
x[2][0]=0.0
x[2][1]=1.0
x[2][2]=0.0
x[2][3]=0.0
x[2][4]=0.0
x[2][5]=0.0
x[3][0]=1.0
x[3][1]=0.0
x[3][2]=0.0
x[3][3]=0.0
x[3][4]=0.0
x[3][5]=0.0
x[4][0]=0.0
x[4][1]=0.0
x[4][2]=0.0
x[4][3]=1.0
x[4][4]=0.0
x[4][5]=0.0
x[5][0]=0.0
x[5][1]=0.0
x[5][2]=0.0
x[5][3]=0.0
x[5][4]=1.0
x[5][5]=0.0
u[0]=0.0
u[1]=2.0
u[2]=1.0
u[3]=5.0
u[4]=4.0
u[5]=3.0
285.1692570340933

最短経路の描画

導出された最適解を描画してみましょう． 隣接行列$x_{ij}$が1となっている部分をエッジとして表示します．

# 経路に含まれるエッジのリスト
edge_list = []

for i in range(len(df)):
    for j in range(len(df)):
        value = x[i][j].varValue
        if value == 1:
            edge = (node_list[i], node_list[j])
            edge_list.append(edge)
            
print(edge_list)

# グラフの作成
graph = nx.DiGraph()
graph.add_nodes_from(node_list)

# 最短経路の描画
graph.add_edges_from(edge_list)
nx.draw(graph, pos=pos_list, with_labels=True)

Image from Gyazo

課題

新たに都市Gを追加し，Aをスタート地点とする巡回セールスマン問題の最短経路を算出しなさい．

# 課題
df_temp = pd.DataFrame({"都市":["G"], "X":[50], "Y":[50]})
df2 = pd.concat([df, df_temp]).reset_index(drop=True)
display(df2)

Image from Gyazo

Image from Gyazo

Image from Gyazo

Jupyter Labで作成したノートブックを保存し，ダウンロードして提出してください． ノートブックをダウンロードするには，メニューから Download を選択します． ノートブックのファイル名は chapter10.ipynb としてください．

愛知県名古屋市にある椙山女学園大学 文化情報学部 向研究室の公式サイトです． 専門は情報科学であり，人工知能やデータベースなどの技術要素を指導しています． この公式サイトでは，授業で使用している教材を公開すると共に， ベールに包まれた女子大教員のミステリアスな日常を４コマ漫画でお伝えしていきます． サイトに関するご意見やご質問はFacebookまたはTwitterでお問い合わせください．