オーバーフィッティングと交差検証
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. また,numpy,matplotlib.pyplot,random,scikit-learn を導入しておいてください.
import numpy as np
import matplotlib.pyplot as plt
import random
from sklearn.model_selection import KFold
オーバーフィッティング(過学習)
オーバーフィッティング とは 過学習 または 過剰適合 と呼ばれることもある現象で, サンプルデータに過剰に適合してしまい, データ全体に対しての汎用的な能力を失った状態を指します. ここでは,回帰問題を例に挙げて,オーバーフィッティングを再現してみましょう.
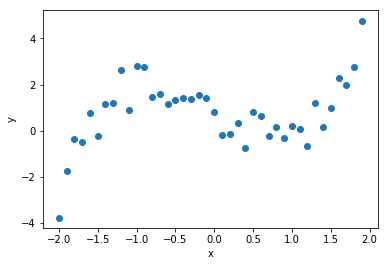
まずは,$x^3 - 2x$に従った40点のデータを生成します. これに,ノイズとなる乱数を加え,対象のデータ全体とします.
x = np.arange(-2, 2, 0.1) # 40点を生成
y = x ** 3 - 2* x
r = np.random.rand(len(y)) * 2 # 乱数を生成
y = y + r # 乱数を加算
data = np.stack([x, y])
plt.scatter(data[0], data[1])
plt.xlabel("x")
plt.ylabel("y")
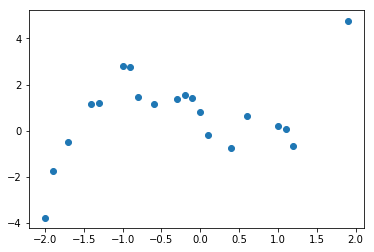
このデータ全体から,20点をランダムに抽出します. これをサンプルデータとして回帰の学習に用いることにします.
sample = np.array(random.sample(list(data.transpose()), 20)).transpose() # 20点をランダム抽出
plt.scatter(sample[0], sample[1])
回帰式の係数の導出にはNumpyのpolyfitを用います.
多項式回帰の次数$d$を変えて回帰式と2乗誤差を求めるため,
新たにregressionという関数を定義します.
関数regressionの返値は回帰式のY軸の値と2乗誤差のタプルです.
def regression(data, sample, d):
w = np.polyfit(sample[0], sample[1], d) #回帰式の係数
y_ = 0
for i in range((d+1)):
y_ += w[i] * (data[0] ** (d - i))
e = sum((data[1] - y_) ** 2) # 2乗誤差
return y_, e
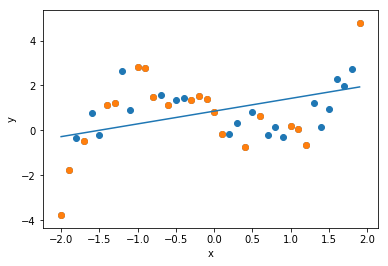
最初に次数$d=1$の回帰式(回帰直線)を求めます. 1本の直線で全体の傾向を近似していることがわかります.
y, e = regression(data, sample, 1)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], y)
plt.xlabel("x")
plt.ylabel("y")
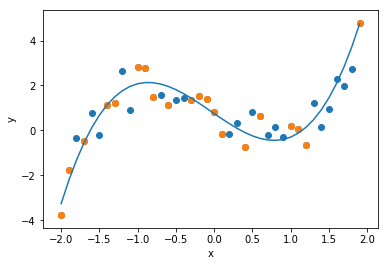
次に次数$d=3$の回帰式を求めます. データにはノイズが加わっていますが, 真の関数である$x^3 - 2x$を,よく近似できていることがわかります.
y, e = regression(data, sample, 3)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], y)
plt.xlabel("x")
plt.ylabel("y")
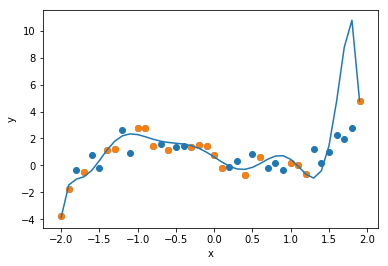
次に次数$d=10$の回帰式を求めます. 一般に次数を上げると近似の精度が上がります. グラフを確認すると,確かにサンプルデータに対しては, 誤差を最小化することができています. しかし,データ全体に対してはどうでしょうか. 上述の$d=3$より近似精度が落ちていないでしょうか.
y, e = regression(data, sample, 10)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], y)
plt.xlabel("x")
plt.ylabel("y")
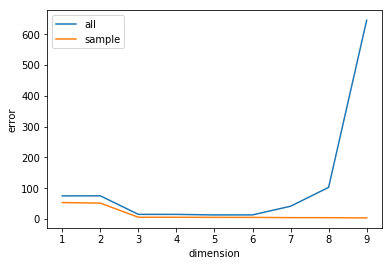
最後に,次数$d$に伴う2乗誤差の推移を可視化してみましょう. 次数が増えるとサンプルデータに対する2乗誤差は減少するのに対し, データ全体に対しては2乗誤差が増加してしまうことがわかります. これが オーバーフィッティング です. これは回帰問題に限らず,サンプルデータを用いて学習する手法では, 起こり得る現象です.
dimension = np.arange(1, 10, 1)
errors_all = [] # データ全体に対する2乗誤差
for i in dimension:
y, e = regression(data, sample, i)
errors_all.append(e)
errors_sample = [] # サンプルに対する2乗誤差
for i in dimension:
y, e = regression(sample, sample, i)
errors_sample.append(e)
plt.plot(dimension, errors_all, label="all")
plt.plot(dimension, errors_sample, label="sample")
plt.xlabel("dimension")
plt.ylabel("error")
plt.legend()
交差検証(クロスバリデーション)
オーバーフィッティングの影響を減らし,回帰式の妥当な精度を得ることを目的として, 交差検証(Cross-Validation) と呼ばれる方法が用いられます. 特に十分なデータセットが用意できないときに,汎用性を向上させる手段として, 有効な方法とされています.
ここでは,機械学習でよく用いられる k-分割交差検証(k-fold cross validation) を取り上げます.
この方法では,データセットをk個に分割し, k-1個 を学習に,残りの 1個 をテストに用います.
KFold関数に分割数$k=5$を指定して分割します(データの順番もシャッフルします).
この結果,5パターンの学習用とテスト用のサンプルが生成されます.
各サンプルは,学習用に32,テスト用に8のデータが用意されていることがわかります.
[IN:]
kf = KFold(n_splits=5, shuffle=True, random_state = 0) #k-分割交差検証(k=5)
for train_set, test_set in kf.split(data[0]):
print("train_set: "+ str(train_set) + " test_set: " + str(test_set))
[OUT:]
train_set: [ 0 1 2 3 4 5 6 8 10 11 12 13 14 15 16 17 18 19 22 24 26 27 28 29
30 32 33 35 36 37 38 39] test_set: [ 7 9 20 21 23 25 31 34]
train_set: [ 0 1 2 3 6 7 8 9 12 15 17 18 19 20 21 22 23 24 25 26 27 28 29 31
32 33 34 35 36 37 38 39] test_set: [ 4 5 10 11 13 14 16 30]
train_set: [ 0 1 2 3 4 5 7 8 9 10 11 12 13 14 16 17 19 20 21 22 23 24 25 28
29 30 31 32 34 36 38 39] test_set: [ 6 15 18 26 27 33 35 37]
train_set: [ 1 2 3 4 5 6 7 9 10 11 13 14 15 16 18 19 20 21 23 24 25 26 27 29
30 31 33 34 35 36 37 39] test_set: [ 0 8 12 17 22 28 32 38]
train_set: [ 0 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 20 21 22 23 25 26 27 28
30 31 32 33 34 35 37 38] test_set: [ 1 2 3 19 24 29 36 39]
次に,KFold関数を利用して,多項式回帰の2乗誤差を求めるvalidate関数を定義します.
5パターンのデータセットで,それぞれ2乗誤差を求め,その 平均値 を最終的な評価とします.
例えば,分割数$k=5$で,3次の多項式回帰の2乗誤差の平均は 2.78 となりました.
def validate(k, dimension):
kf = KFold(n_splits=k, shuffle=True, random_state = 0)
errors = []
for train_set, test_set in kf.split(data[0]):
train = np.array([data[0][train_set], data[1][train_set]])
test = np.array([data[0][test_set], data[1][test_set]])
y, e = regression(test, train, dimension)
errors.append(e)
avg = np.mean(errors) # 2乗誤差の平均
return avg
[IN:]
avg = validate(5, 3) # 5分割, 3次の多項式回帰
print("Average Error: " + str(avg))
[OUT:]
Average Error: 2.781161227904894
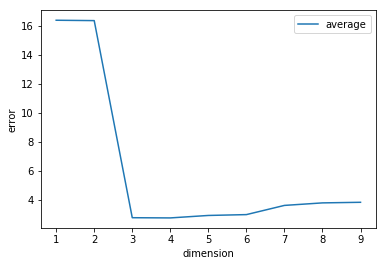
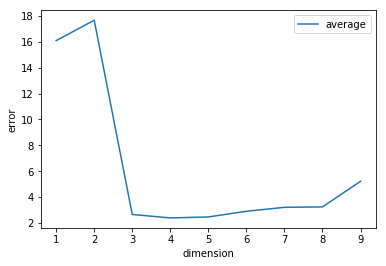
最後に,k-分割交差検証を利用して,次数$d$に伴う2乗誤差の推移を可視化してみましょう. 全体的な傾向はk-分割交差検証を用いない場合と同様ですが, オーバーフィッティングの影響が小さくなるため, 次数が増えても2乗誤差は極端に増加していません.
dimension = np.arange(1, 10, 1)
errors_avg = []
for i in dimension:
e = validate(5, i)
errors_avg.append(e)
plt.plot(dimension, errors_avg, label="average")
plt.xlabel("dimension")
plt.ylabel("error")
plt.legend()
課題
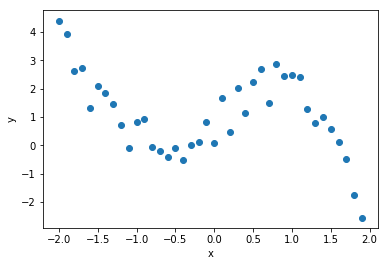
下記のデータセットを利用し,$k=5$のk-分割交差検証で多項式回帰の精度を評価しなさい.
x2 = np.array([-2.00000000e+00, -1.90000000e+00, -1.80000000e+00, -1.70000000e+00,
-1.60000000e+00, -1.50000000e+00, -1.40000000e+00, -1.30000000e+00,
-1.20000000e+00, -1.10000000e+00, -1.00000000e+00, -9.00000000e-01,
-8.00000000e-01, -7.00000000e-01, -6.00000000e-01, -5.00000000e-01,
-4.00000000e-01, -3.00000000e-01, -2.00000000e-01, -1.00000000e-01,
1.77635684e-15, 1.00000000e-01, 2.00000000e-01, 3.00000000e-01,
4.00000000e-01, 5.00000000e-01, 6.00000000e-01, 7.00000000e-01,
8.00000000e-01, 9.00000000e-01, 1.00000000e+00, 1.10000000e+00,
1.20000000e+00, 1.30000000e+00, 1.40000000e+00, 1.50000000e+00,
1.60000000e+00, 1.70000000e+00, 1.80000000e+00, 1.90000000e+00])
y2 = np.array([ 4.39898556e+00, 3.93435081e+00, 2.61498259e+00, 2.72044213e+00,
1.30362037e+00, 2.08098975e+00, 1.85633410e+00, 1.44865881e+00,
7.29089005e-01, -9.42380345e-02, 8.39806492e-01, 9.13725511e-01,
-6.89556978e-02, -1.88622122e-01, -4.17447107e-01, -8.50096595e-02,
-5.10447688e-01, -1.18019152e-03, 1.36162277e-01, 8.31331709e-01,
9.37694167e-02, 1.68726072e+00, 4.71255186e-01, 2.02384997e+00,
1.12543648e+00, 2.23950532e+00, 2.69476804e+00, 1.50769218e+00,
2.86140345e+00, 2.46208705e+00, 2.46640709e+00, 2.40690140e+00,
1.29052071e+00, 7.78084009e-01, 1.01201918e+00, 5.94619852e-01,
1.27863784e-01, -4.80496436e-01, -1.75028230e+00, -2.54273399e+00])
data2 = np.stack([x2, y2])
課題を完成させたら,ノートブックを保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定