分類③・ロジスティック回帰

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter9 とします． また，numpy，matplotlib.pyplot，scipy.optimize を導入しておいてください．

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

データの準備

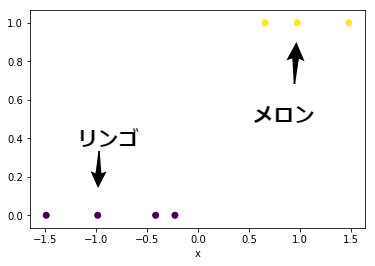
これまでは，リンゴとメロンの 大きさ（$x_1$） と 重さ（$x_2$） という2次元のデータを用いていました． 今回は単純化のため，大きさ（$x$） のみに注目して分類します． また，グラフで可視化するために，リンゴを$0$，メロンを$1$と表現することにします．

x = np.array([9.5, 11.2, 10.3, 11.5, 13.4, 12.9, 14.2]) #大きさ（cm）
label = np.array([0, 0, 0, 0, 1, 1, 1]) #カテゴリ
x = (x - x.mean()) / x.std() #標準化
plt.scatter(x, label, c=label)
plt.xlabel("x")

ロジスティック回帰

今回取り上げる手法は ロジスティック回帰 です． 「回帰」という文字列が含まれますが，実際は前回の線形判別分析と同様に 分類 を目的とした手法です． 確率モデルとして用いられる ロジスティック関数（シグモイド関数） に， 対象のデータを回帰させることから，その名前が付けられています．

ロジスティック関数

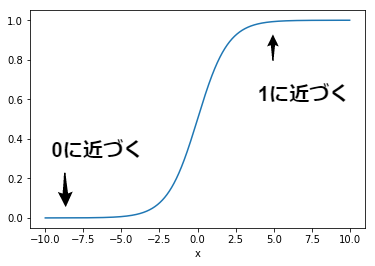
まずは，ロジスティック関数$p(x)$の定義を確認しましょう． ロジスティック関数$p(x)$は，$x$が増加すると$1$に漸近し，また，$x$が減少すると$0$に漸近するという特徴を持ちます．

$$ p(x) = \frac{1}{1 + e^{-x}} $$

def px(x):
    value = 1 / (1 + np.exp(-x))
    return value

x_ = np.arange(-10, 10, 0.01)
y_ = px(x_)
plt.plot(x_,y_)    
plt.xlabel("x")

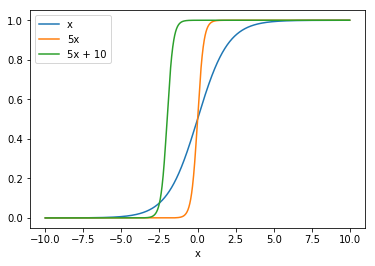
次に，入力$x$に依存して，関数の形状がどのように変化するか見てみましょう． 下記のグラフは$x$，$5x$，$5x + 10$を入力としたときのロジスティック関数の比較です． 入力が変化すると，傾き や 変曲点の位置 が変わることがわかります．

$$ p(5x) = \frac{1}{1 + e^{-(5x)}} $$

$$ p(5x + 10) = \frac{1}{1 + e^{-(5x + 10)}} $$

x_ = np.arange(-10, 10, 0.01)

y1_ = px(x_)
y2_ = px(5 * x_)
y3_ = px(5 * x_ + 10)

plt.plot(x_,y1_, label="x")
plt.plot(x_,y2_, label="5x")
plt.plot(x_,y3_, label="5x + 10")
plt.xlabel("x")
plt.legend() #判例を表示

そこで，ロジスティック関数の入力の一般式$f(x)$を下記のように定義します． $w_1$は傾き，$w_0$は変曲点の位置を決めるパラメータです． これらのパラメータを調整することで，ロジスティック関数の形状を自由に変えることができます．

$$ f(x) = w_1 \cdot x + w_0 $$

$$ p(f(x)) = p(w_1 \cdot x + w_0) = \frac{1}{1 + e^{-(w_1 \cdot x + w_0)}} $$

尤度

次にもっともらしさを表す指標である 尤度 について考えます． ロジスティック回帰では，この 尤度 を最大化するようなパラメータを求めることが目的となります．

最初に，$f(x)=x$を入力とした場合を考えます（$w_1 = 1$，$w_0 = 0$ ）． このとき，リンゴとメロンの大きさ$x$に対する，ロジスティック関数$p(x)$の値を計算します．

[In:]

p = px(1*x + 0)
print(x)
print(p)
print(1-p)

[Out:]

[-1.49090975 -0.41564757 -0.98490402 -0.22589542  0.9758682   0.65961462
  1.48187394]
[0.18378522 0.39755872 0.2719198  0.44376508 0.72628761 0.65917381
 0.81485546]
[0.81621478 0.60244128 0.7280802  0.55623492 0.27371239 0.34082619
 0.18514454]

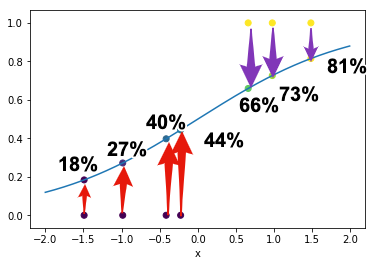
計算された値は，ロジスティック関数の特徴から，$0$から$1$の範囲に収まります． ロジスティック回帰では，この値を 大きさが$x$であるときのメロンである確率 とみなします． 例えば，$x=-1.49$がメロンである確率は$18.4\%$， $x=0.98$がメロンである確率は$72.6\%$となります． また，大きさが$x$であるときのリンゴである確率 は $1-p(x)$であるため， 例えば，$x=-1.49$がリンゴである確率は$81.6\%$， $x=0.98$がリンゴである確率は$27.4\%$となります．

x_ = np.arange(-2, 2, 0.01)
y_ = px(x_)
p = px(x)
plt.scatter(x, label, c=label)
plt.scatter(x, p, c=p)
plt.plot(x_,y_)
plt.xlabel("x")

このときの尤度$L(x)$は下記のように定義します． 尤度は，$x_1 \cdots x_4$がリンゴ，また，$x_5 \cdots x_7$がメロンであるときの尤もらしさを表現しています． つまり，前方の4つの項は，$x_1 \cdots x_4$がリンゴであるときの同時確率， また，後方の3つの項は，$x_5 \cdots x_7$がメロンであるときの同時確率であり， これらの同時確率を掛け合わせた値が尤度$L(x)$となります．

$$ L(x) = (1 - p(x_1)) \cdot (1 - p(x_2)) \cdot (1 - p(x_3)) \cdot (1 - p(x_4)) \cdot p(x_5) \cdot p(x_6) \cdot p(x_7) $$

$$ L(x) = 0.82 \cdot 0.60 \cdot 0.72 \cdot 0.56 \cdot 0.73\cdot 0.66 \cdot 0.81 $$

$$ L(x) =0.078 $$

[In:]

def lx(w, x): #尤度
    apple = np.where(label==0)
    melon = np.where(label==1)
    p_apple = np.prod(1 - px(w[1] * x[apple] + w[0])) #リンゴである確率
    p_melon = np.prod(px(w[1] * x[melon] + w[0])) #メロンである確率
    l = p_apple * p_melon
    return l

w = np.array([0, 1])
l = lx(w, x)
print(l)

[Out:]

0.07768654594308204

ここで，求めたのは$w_1=1$，$w_0=0$のときの尤度$L(x)$です． 当然，このパラメータの値が変われば，尤度の値も変わります． そこで，尤度$L(x)$を最大化するような，$w_1$，$w_0$を求めます． このような手法は 最尤推定 と呼ばれ，ロジスティック回帰で主に用いられます．

数値解の導出

それでは，数値解を導出してみましょう． 前回も用いた minimize 関数を利用します． 今回も目的は尤度の 最大化 です． そこで，符号を反転した目的関数$g(x)$を定義しています． 求めた数値解は$w_0 = -8.95$，$w_1 = 34.54$です． このパラメータで尤度を求めると$L(x) \simeq 1$となり， ロジスティック関数で，ほぼ正確に回帰（近似）できたことが分かります．

[In:]

def gx(w, x):
    value = -1 * lx(w, x)
    return value

w_init = np.array([0, 1])
result = minimize(gx, w_init, args=(x), method="SLSQP")
print(result.x)

[Out:]

[-8.94836536 34.53672525]

[In:]

w = result.x
print(lx(w, x))

[Out:]

0.99999896366082

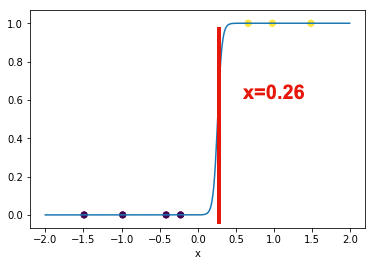
最後にグラフを描いて可視化してみましょう． ロジスティック関数により，リンゴとメロンが正確に分類されていることがわかります． 決定境界は$f(x) = 34.54 \cdot x - 8.95 = 0$を解くことで求めることができます． これは，ロジスティック関数の変曲点の値が1/2であることが理由です． これを解くと$x = 0.26$となり，$x<0.26$であればリンゴ，$x>0.26$であれば メロンと分類することができます．

x_ = np.arange(-2, 2, 0.01)
y_ = px(w[1] * x_ + w[0])
p = px(w[1] * x + w[0])
plt.scatter(x, label, c=label)
plt.scatter(x, p, c=p)
plt.plot(x_,y_)
plt.xlabel("x")

課題

下記のデータを分類する決定境界をロジスティック回帰で求めよ．

x = np.array([10, 13, 15, 19, 23, 25])
label = np.array([1, 1, 1, 0, 0, 0])

課題を完成させたら，chapter9.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定