分類②・線形判別分析

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter8 とします． また，numpy，matplotlib.pyplot，scipy.optimize を導入しておいてください．

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

データの準備

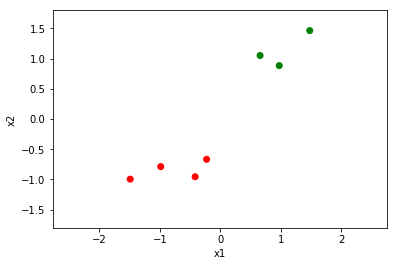
前回と同じリンゴとメロンの 大きさ（$x_1$） と 重さ（$x_2$） を用います（未知のデータ$u$をリンゴとしてデータに追加）． 各要素はベクトル${\bf x} = (x_1,x_2)$として表すことに注意してください． ここでは，あらかじめデータを標準化しておきます．

[In:]

x1 = np.array([9.5, 11.2, 10.3, 11.5, 13.4, 12.9, 14.2]) #大きさ（cm）
x2 = np.array([278, 298, 382, 443, 1221, 1305, 1512]) #重さ（g）
label = np.array(["red","red","red","red","green","green","green"]) #カテゴリ
x1 = (x1 - x1.mean()) / x1.std()
x2 = (x2 - x2.mean()) / x2.std()
print(x1)
print(x2)

[Out:]

[-1.49090975 -0.41564757 -0.98490402 -0.22589542  0.9758682   0.65961462
  1.48187394]
[-0.99454837 -0.95468671 -0.78726775 -0.66568969  0.88492881  1.05234778
  1.46491594]

plt.scatter(x1, x2, c=label)
plt.gca().set_aspect("equal", "datalim")
plt.ylim([-1.8, 1.8])
plt.xlabel("x1")
plt.ylabel("x2")

線形判別分析

前回は 分類 における 決定境界 と ベクトル の役割について解説しました． 今回は，決定境界を決めるベクトル${\bf w}=(w_1, w_2)$の導出方法について考えます． 分類のためのアルゴリズムは様々ありますが，今回は 線形判別分析（Linear Discriminant Analysis: LDA） に挑戦してみましょう． 線形判別分析は，データを分類するために，線形（直線） の決定境界を求める方法です．

代表ベクトル

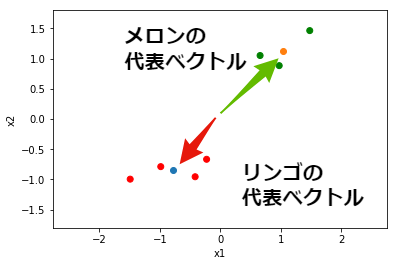
まず最初に，各ラベル（ここでは，リンゴとメロン）の 代表ベクトル を求めます． 代表ベクトルとは重心（平均）のことです． ここで，リンゴの代表ベクトルを${\bf a} = (a_1, a_2)$， メロンの代表ベクトルを${\bf m} = (m_1, m_2)$と表すことにします． 下記のように計算すると，${\bf a} = (-0.78, -0.85)$，${\bf m} = (1.04, 1.13)$となります．

$$ (a_1, a_2) = \left( \frac{-1.49 + -0.42 + -0.98 + -0.23}{4}, \frac{-0.99 + -0.95 + -0.79 + -0.67}{4} \right) $$

$$ (m_1, m_2) = \left( \frac{0.98 + 0.66 + 1.48}{3}, \frac{0.88 + 1.05 + 1.46}{3} \right) $$

[In:]

apple = np.where(label=="red") #リンゴのインデックスを取得
melon = np.where(label=="green") #メロンのインデックスを取得
a = np.array([x1[apple].mean(),x2[apple].mean()])
m = np.array([x1[melon].mean(),x2[melon].mean()])
print(a)
print(m)

[Out:]

[-0.77933919 -0.85054813]
[1.03911892 1.13406417]

plt.scatter(x1, x2, c=label)
plt.scatter(a[0], a[1])
plt.scatter(m[0], m[1])
plt.gca().set_aspect("equal", "datalim")
plt.ylim([-1.8, 1.8])
plt.xlabel("x1")
plt.ylabel("x2")

決定境界

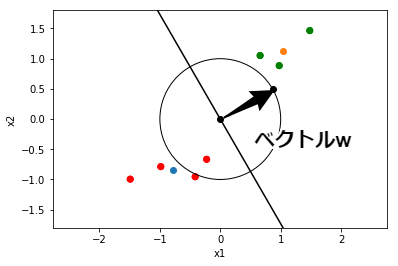
次に，決定境界を決めるベクトル${\bf w}=(w_1, w_2)$について考えます． 前回は${\bf w}=(1, 1)$と勝手に決めてしまいましたが， 線形判別分析では，下記の条件を満たす$w_1$と$w_2$の組み合わせに限定することにします．

$$ |{\bf w}| = w_1^2 + w_2^2 = 1 $$

これは，半径$1$の円周上にベクトル${\bf w}$があることを意味しています． つまりベクトルの 大きさ は固定して，ベクトルの 回転 に注目するということです． 例えば，${\bf w} = \left( \cos(\pi / 6), \sin(\pi / 6) \right) = \left( \frac{\sqrt{3}}{2}, \frac{1}{2} \right)$ は，この条件を満たしています． このとき，決定境界は $x_2 = - \sqrt{3} \cdot x_1$ となります（前回の資料を参照すること）．

[In:]

w1 = np.sqrt(3) / 2
w2 = 1 / 2
w = np.array([w1, w2])
np.linalg.norm(w, ord=2) #ユークリッド距離(ord=2)

[Out:]

0.9999999999999999

目的関数

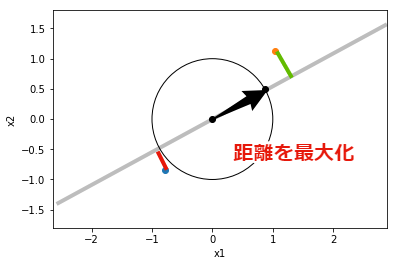
最適な${\bf w}=(w_1, w_2)$を求めるための目的関数を定めます． ここでも内積の概念を利用します． ベクトル${\bf w}$と，リンゴとメロンの代表値である${\bf r}$と${\bf m}$の内積を求めます． $|{\bf w}|=1$であることから，内積はベクトル${\bf w}$に対する，ベクトル${\bf r}$と${\bf m}$の正射影になります． 正射影された2点間の距離を目的関数$g({\bf w})$とし，これが最大となる${\bf w}=(w_1, w_2)$を求めます． 例えば，${\bf w} =\left( \frac{\sqrt{3}}{2}, \frac{1}{2} \right)$ のときは，$g({\bf w}) = 2.57$となります．

$$ g(w) = |{\bf w} \cdot {\bf a} - {\bf w} \cdot {\bf m}| $$

[In:]

# 正射影された2点間の距離
def gw(w, a, m):
  d = np.abs(w.dot(a) - w.dot(m))
  return d

gw(w, a, m)

[Out:]

2.5671370685019306

数値解の導出

最後に数値解を求めていきましょう． 回帰で用いた minimize 関数を利用しますが，少し工夫が必要です．

まず，今回の目的は，$g({\bf w})$の 最大化 が目的です． しかし，minimize関数は 最小化 することしか出来ません． そこで，$g({\bf w})$の符号を反転した目的関数を新たに定義します． 負の値を最小化することは，元の正の値を最大化することに等しくなります．

次に，$|{\bf w}| = 1$を表す条件式を定義します． しかし，minimize関数では，eqという比較演算子で条件を定義する必要があり， この比較演算子は「== 0」を意味します． このため，条件式は$|{\bf w}| - 1 == 0$と変形する必要があります．

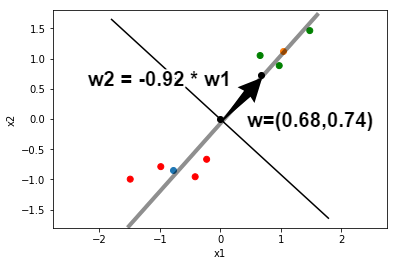
この制約条件の基で，目的関数を最大化すると， ${\bf w} = (0.68, 0.74)$が解として求まります． 決定境界は$x_2 = - 0.92 \cdot x_1$となり， リンゴとメロンを適切に分類出来ていることがわかります．

[In:]

#目的関数（最小化するため符号を反対に）
def gw2(w, a, m):
  d = -1 * gw(w, a, m)
  return d

#条件式（ベクトル長から1を引く）
def norm(w):
  l = np.linalg.norm(w, ord=2) #ベクトルの大きさ
  return l - 1

#制約条件（eqは0と等しいことを表す）
cons = (
  {"type": "eq", "fun": norm}
)

w_init = w
result = minimize(gw2, w_init, args=(a, m), constraints=cons, method="SLSQP")
print(result.x)

[Out:]

[0.67569856 0.73717806]

最後に決定境界を求めプロットしてみましょう．

x1_ = np.arange(-3, 3, 0.01)
x2_ = -1 * (result.x[0] / result.x[1]) * x1_
plt.plot(x1_, x2_) #決定境界
plt.scatter(x1, x2, c=label)
plt.scatter(a[0], a[1])
plt.scatter(m[0], m[1])
plt.gca().set_aspect("equal", "datalim")
plt.ylim([-1.8, 1.8])
plt.xlabel("x1")
plt.ylabel("x2")

課題

下記のデータを分類する決定境界を線形判別分析で求めてください．

x1 = np.array([10, 13, 15, 19, 23, 25])
x2 = np.array([17, 18, 18, 16, 17, 16])
label = np.array(["blue","blue","blue","pink","pink","pink"]) #カテゴリ

課題を完成させたら，chapter8.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定