分類①・決定境界とベクトル
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter7 とします. また,numpy,matplotlib.pyplot,scipy.optimize を導入しておいてください.
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
分類
今回からは 分類 と呼ばれる問題にチャレンジします. これまでの 回帰 では,「アイスクリームの売上」や「インフルエンザの報告数」など連続値を予測対象としましたが, 分類では「リンゴ or メロン」や「Aさんの顔 or Bさんの顔」など離散値を予測対象とします. これら目標データとなる離散値を ラベル,カテゴリ ,または,クラス と呼びます.
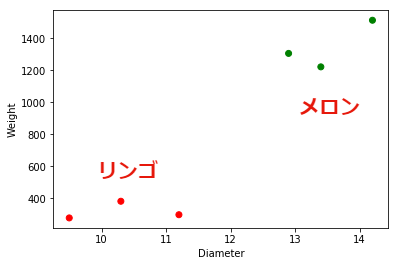
ここでは,下記のデータを例に考えてみましょう. このデータはリンゴとメロンの 大きさ($x_1$) と 重さ($x_2$) を示しています. カテゴリは色で表現されており,red はリンゴ, green はメロンを表しています. 例えば,$x_1=9.5$,$x_2=278$ はリンゴであることを意味します.
x1 = np.array([9.5, 11.2, 10.3, 13.4, 12.9, 14.2]) #大きさ(cm)
x2 = np.array([278, 298, 382, 1221, 1305, 1512]) #重さ(g)
label = np.array(["red","red","red","green","green","green"]) #カテゴリ
plt.scatter(x1, x2, c=label) #カテゴリで色付け
plt.xlabel("Diameter")
plt.ylabel("Weight")
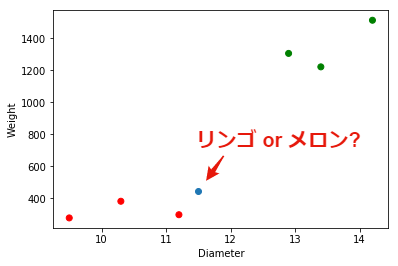
未知のデータ $u_1=11.5$,$u_2=443$が与えられたとき, これはリンゴでしょうか,それともメロンでしょうか. これを当てるのが 分類 と呼ばれる問題です.
u1 = 11.5
u2 = 443
plt.scatter(x1, x2, c=label)
plt.scatter(u1, u2)
plt.xlabel("Diameter")
plt.ylabel("Weight")
分類 のためのアルゴリズムには,線形判別分析,ロジスティック回帰,決定木 などのアルゴリズムがあります. 今回は,分類を理解するために必要な 決定境界 と ベクトル の関係について学びます.
決定境界とベクトル
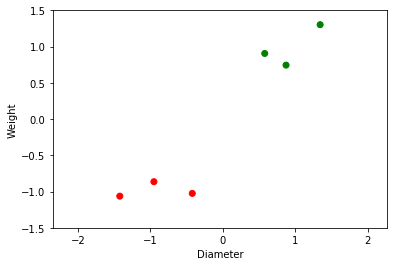
では,分類問題をどのように解けば良いか考えていきましょう. まずは,大きさと重さのデータを 標準化 します. 標準化とは平均を$0$,標準偏差(分散)を$1$に変換する操作を指します. 平均は mean 関数 ,標準偏差は std 関数で求めます. ここで,平均を$\mu$,標準偏差を$\sigma$とすると,標準化は下記の式で与えられます.
$$ x’ = \frac{(x - \mu)}{\sigma} $$
x1 = (x1 - x1.mean()) / x1.std()
x2 = (x2 - x2.mean()) / x2.std()
plt.scatter(x1, x2, c=label)
plt.gca().set_aspect('equal', 'datalim') #縦横比を1:1に変更
plt.ylim([-1.5, 1.5]) #Y軸の範囲
plt.xlabel("Diameter")
plt.ylabel("Weight")
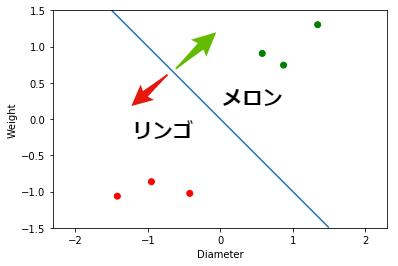
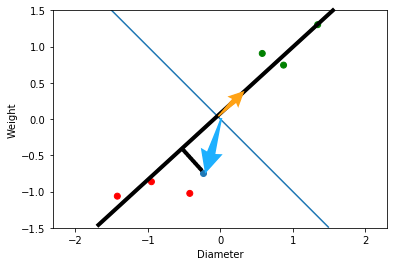
リンゴとメロンはどのように分類することができるでしょうか. 結論を先に述べると下図に示すような境界線を見つければ良いということになります. この境界線を 決定境界 と呼びます. この図の場合は,決定境界より左下にあれば リンゴ,右上にあれば メロン と分類すれば良いことになります.
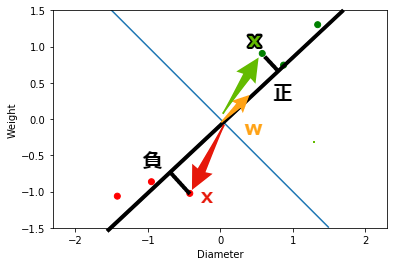
ここで,この決定境界に直交するベクトル${\bf w} = (w_1, w_2)$を考えます. このベクトル${\bf w}$と,大きさと重さを表すベクトル${\bf x} = (x_1, x_2)$の内積を計算します. ベクトルの内積は下記のように定義されます($\theta$は${\bf w}$と${\bf x}$のなす角).
$$ f({\bf x}) = {\bf w} \cdot {\bf x} = w_1 \cdot x_1 + w_2 \cdot x_2 = |{\bf w}| \cdot |{\bf x}| \cdot \cos(\theta) $$
内積は,ベクトル${\bf w}$に対して,ベクトル${\bf x}$を垂直に下ろした, 正射影 を表します(正確には$|{\bf w}| = 1$のとき). ここでの,ポイントは内積した値の 符号 です. 符号が 正 であるとき,$0 < \theta < \frac{1}{2}\pi$, または,$\frac{3}{2}\pi < \theta < 2 \pi$であり,${\bf x}$はメロンとみなすことができます. 一方,符号が 負 であるとき, $\frac{1}{2}\pi < \theta < \frac{3}{2}\pi$であり, ${\bf x}$はリンゴとみなすことができます. このような関数$f({\bf x})$を 識別関数 と呼びます.
また,ベクトル${\bf w}$は決定境界と直交しているため,決定境界を表すベクトル${\bf x}$との内積は$0$になります($\cos(\pi / 2) = 0$であるため). これを変形すると,決定境界の直線を表す式を得ることができます.
$$ {\bf w} \cdot {\bf x} = w_1 \cdot x_1 + w_2 \cdot x_2 = 0 $$
$$ x_2 = -\frac{w_1}{w_2} \cdot x_1 $$
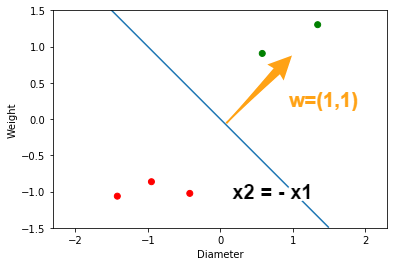
具体例を考えましょう. ベクトル${\bf w} = (1, 1)$とします. すると,決定境界を表す直線は,$x_2 = - x_1$となります.
$$ x_2 = -\frac{1}{1} \cdot x_1 = -x_1 $$
x1_ = np.arange(-1.5, 1.5, 0.01)
x2_ = -1 * x1_
plt.scatter(x1, x2, c=label)
plt.plot(x1_, x2_)
plt.gca().set_aspect('equal', 'datalim')
plt.ylim([-1.5, 1.5]) #Y軸の範囲
plt.xlabel("Diameter")
plt.ylabel("Weight")
次に${\bf w}$と${\bf x}$の内積を計算します. 内積は dot 関数を用います. するとリンゴを表すベクトルとの内積は 負の値 ,メロンを表すベクトルとの内積は 正の値 になっていることが分かります. これにより,ベクトル${\bf w} = (1, 1)$とした識別関数 $f(x)$ は,リンゴとメロンを正しく分類できていることが示されました.
[In:]
w = np.array([1,1])
x = np.array([x1, x2])
p = w.dot(x) #内積(識別関数)
print(p)
[Out:]
[-2.48474564 -1.44663783 -1.81486073 1.61693019 1.48394489 2.64536912]
#リンゴ リンゴ リンゴ メロン メロン メロン
では,未知のデータ$u_1=11.5$,$u_2=443$ではどうでしょうか. $x_1$,$x_2$と同様に標準化し,ベクトル${\bf w} = (1, 1)$との内積を計算します. すると,$-0.99$となり,これは負の値であるため, リンゴ であると分類されることになります.
x1 = np.array([9.5, 11.2, 10.3, 13.4, 12.9, 14.2]) #平均と標準偏差を求めるため
x2 = np.array([278, 298, 382, 1221, 1305, 1512]) #平均と標準偏差を求めるため
u1 = (u1 - x1.mean()) / x1.std()
u2 = (u2 - x2.mean()) / x2.std()
u = np.array([u1, u2])
p = w.dot(u) #内積
print(p)
-0.9921864664330837
今回設定した${\bf w} = (1, 1)$は,たまたま上手く分類が出来ました. 一般的な分類アルゴリズムでは,適切な${\bf w}$を求めることが狙いとなります. 次回は,ベクトルの内積の考えを利用した 線形判別分析 に挑戦します.
課題
下記のデータを分類する決定境界(ベクトル${\bf w}$)を自由に定め, 識別関数$f(x)$の結果が正しいことを示してください.
x1 = np.array([10, 13, 15, 19, 23, 25])
x2 = np.array([17, 18, 18, 16, 17, 16])
label = np.array(["blue","blue","blue","pink","pink","pink"]) #カテゴリ
課題を完成させたら,chapter7.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定