リッジ回帰とラッソ回帰
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter6 とします. また,numpy,random, matplotlib.pyplot,scipy.optimizeを導入しておいてください.
import numpy as np
import random
import matplotlib.pyplot as plt
from scipy.optimize import minimize
オーバーフィッティング(過学習)
オーバーフィッティング とは 過学習 または 過剰適合 と呼ばれることもある現象で, サンプルデータに過剰に適合してしまい, データ全体に対しての汎用的な能力を失った状態を指します. ここでは,回帰問題を例に挙げて,オーバーフィッティングを再現してみましょう.
ここでは,$x^3 - 2x$にノイズとなる乱数を加えた40点のデータを生成します.
x = np.array([-2. ,-1.9,-1.8,-1.7,-1.6,-1.5,-1.4,-1.3,-1.2,-1.1,-1. ,-0.9,-0.8,-0.7, -0.6,-0.5,-0.4,-0.3,-0.2,-0.1, 0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. , 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9])
y = np.array([-3.75,-2.28,-1.16,-1.08,-0.89,-0.08, 0.58, 1.69, 1.6 , 2.17, 2.61, 1.42, 1.33, 1.26, 2.46, 1.5 , 1.42, 1.69, 0.6 , 1.76, 0.55, 1.33, 0.63, 0.93, 0.24, 0.66, 0.08,-0.47, 0.58,-0.76,-0.85, 0.5 ,-0.6 , 1.53, 1.63, 1.46, 0.94, 3.41, 2.99, 5.03])
data = np.stack([x, y])
plt.scatter(data[0], data[1])
plt.xlabel("x")
plt.ylabel("y")
このデータ全体から,ランダムに抽出した20点を回帰の学習に用いることにします.
x = np.array([-0.8, 1.2, 0. , 1.9, 0.4,-0.3,-2. ,-1.5,-1.7, 0.2,-0.6, 0.1, 1.1,-0.5, -1.3,-0.1,-1. , 0.6,-1.1,-1.9])
y = np.array([ 1.33,-0.6 , 0.55, 5.03, 0.24, 1.69,-3.75,-0.08,-1.08, 0.63, 2.46, 1.33, 0.5 , 1.5 , 1.69, 1.76, 2.61, 0.08, 2.17,-2.28])
sample = np.stack([x, y])
plt.scatter(data[0], data[1])
plt.scatter(sample[0], sample[1])
plt.xlabel("x")
plt.ylabel("y")
回帰式の係数の導出にはNumpyのpolyfitを用います.
多項式基底の次数$d$を変えて回帰式と2乗誤差を求めるため,
新たにregressionという関数を定義します.
関数regressionの返値は回帰式のY軸の値と2乗誤差のタプルです.
def regression(data, sample, d):
# サンプルで回帰式の係数
w = np.polyfit(sample[0], sample[1], d)
# f(x)を算出
fx = 0
for i in range((d+1)):
fx += w[i] * (data[0] ** (d - i))
# 平均2乗誤差
e = sum((data[1] - fx) ** 2) / len(data[1])
return fx, e
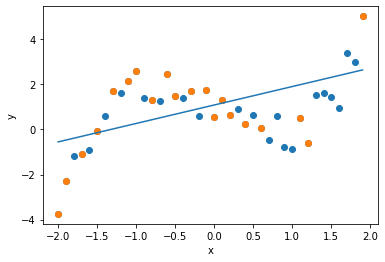
最初に次数$d=1$の回帰式(回帰直線)を求めます. 1本の直線で全体の傾向を近似していることがわかります.
fx, e = regression(data, sample, 1)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], fx)
plt.xlabel("x")
plt.ylabel("y")
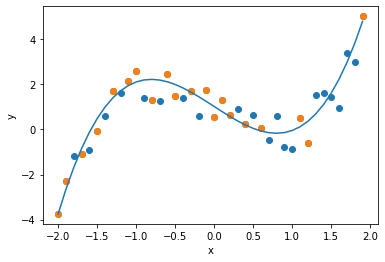
次に次数$d=3$の回帰式を求めます. データにはノイズが加わっていますが, 真の関数である$x^3 - 2x$を,よく近似できていることがわかります.
fx, e = regression(data, sample, 3)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], fx)
plt.xlabel("x")
plt.ylabel("y")
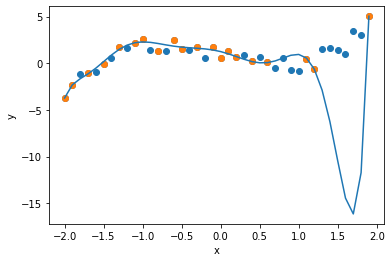
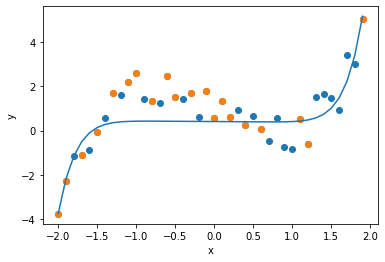
次に次数$d=9$の回帰式を求めます. 一般に次数を上げると近似の精度が上がります. グラフを確認すると,確かにサンプルデータに対しては, 誤差を最小化することができています. しかし,データ全体に対してはどうでしょうか. 上述の$d=3$より近似精度が落ちていないでしょうか.
fx, e = regression(data, sample, 9)
print("Error: " + str(e))
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], fx)
plt.xlabel("x")
plt.ylabel("y")
次数が増えるとサンプルデータに対する誤差は減少するのに対し, データ全体に対しては誤差が増加してしまうことがわかります. これが オーバーフィッティング です. これは回帰問題に限らず,サンプルデータを用いて学習する手法では, 起こり得る現象です.
正則化
オーバーフィッティングを回避する方法の一つに正則化(Regularization)があります. 学習したモデルが複雑になりすぎないように,目的関数(誤差関数)に制約を設ける方法が一般的です. 回帰においては,リッジ回帰(L2ノルム) と ラッソ回帰(L1ノルム) がよく知られています. ノルムを理解するには冬眠氏のブログ「正則化をなるべく丁寧に理解する - 理屈編 -」 がとても参考になります.
平均二乗誤差(正則化なし)
ここでは,上述のように次数$d=9$の多項式基底を考えます. 多項式基底の回帰式$f(x)$を次の関数で定義します.
# 多項式基底
def polynominal(w, x, d):
fx = 0
for i in range(d+1):
fx += w[i] * (x ** i)
return fx
目的関数として平均二乗誤差(Mean Square Error: MSE)を定義します. $y$と$f(x)$の二乗誤差の平均値です.
$$MSE=\frac{1}{N} \sum_{n=0}^{N-1} (y_n - f(x_n))^2$$
# 平均二乗誤差
def mse(w, x, y, d):
y_ = polynominal(w, x, d)
error = np.sum((y - y_) ** 2) / len(y_)
return error
minimize 関数を利用して,平均二乗誤差を最小化する重み $w$ を算出します. このとき次数$d$は9に設定します.
d = 9 # 次数
w_init = np.ones(d+1)
result = minimize(mse, w_init, args=(sample[0], sample[1], d), method="powell")
w = result.x
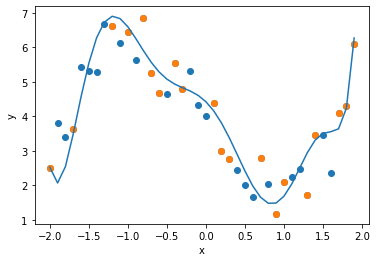
算出された重み$w$を用いて,回帰式をグラフで表します. polyfit と同様に正則化を加えていない状態では, オーバーフィッティングが生じていることが確認できます.
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], polynominal(w, data[0], d))
plt.xlabel("x")
plt.ylabel("y")
リッジ回帰
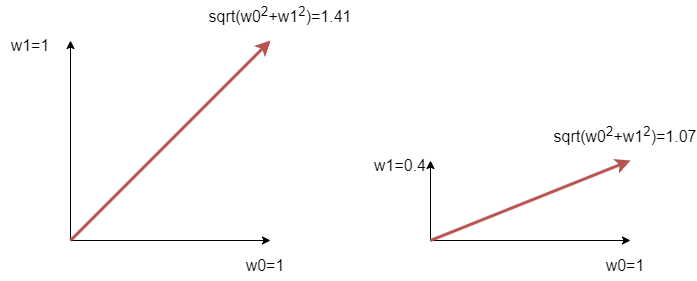
次にリッジ回帰(Ridge Regression)で回帰式を求めます. リッジ回帰では,目的変数として,平均二乗誤差にL2ノルムの正則化項を加算します. L2ノルムはユークリッド距離を表しており,ここでは重みベクトル$w$の長さを表します(平方根は計算しないけど). 正則化により,重みは過剰に大きくならないように制約されます. ここで,$\lambda$は正則化のバランスを調整する係数です.
$$RIDGE=\frac{1}{N} \sum_{n=0}^{N-1} (y_n - f(x_n))^2 + \lambda \sum_{d=0}^{D-1} w_d^2$$
リッジ回帰の目的関数を定義します.
# 正則化を加えた平均二乗誤差(リッジ回帰)
def ridge(w, x, y, d, lam):
y_ = polynominal(w, x, d)
error = np.sum((y - y_) ** 2) / len(y_) + lam * np.sum(w ** 2)
return error
先程と同様に minimize 関数で,リッジ回帰の目的関数を最小化する重み$w$を算出します. このとき,次数$d=9$,正則化の係数$\lambda=1$に設定しています.
d = 9 # 次数
lam = 1 # 正則化項の係数
w_init = np.ones(d+1)
result = minimize(ridge, w_init, args=(sample[0], sample[1], d, lam), method="powell")
w = result.x
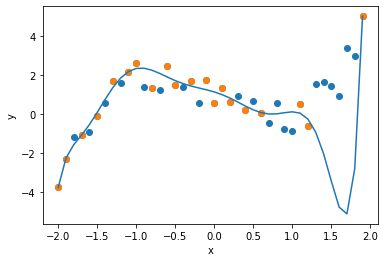
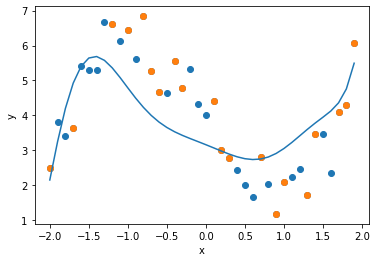
算出された重み$w$を用いて,回帰式をグラフで表します. オーバーフィッティングが回避され,全体の傾向を近似した回帰式が導出されていることが確認できます.
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], polynominal(w, data[0], d))
plt.xlabel("x")
plt.ylabel("y")
ラッソ回帰
最後にラッソ回帰(Lasso Regression)で回帰式を求めます. ラッソ回帰では,目的変数として,平均二乗誤差にL1ノルムの正則化項を加算します. L1ノルムはマンハッタン距離を表しており,ここでは重みベクトル$w$の絶対値の和で求められます. 正則化により,不要な変数の重みが0になるように調整されます(特徴量選択と考えることもできる). ここで,$\lambda$は正則化のバランスを調整する係数です.
$$LASSO=\frac{1}{N} \sum_{n=0}^{N-1} (y_n - f(x_n))^2 + \lambda \sum_{d=0}^{D-1} |w_d|$$
ラッソ回帰の目的関数を定義します.
# 正則化を加えた平均二乗誤差(ラッソ回帰)
def lasso(w, x, y, d, lam):
y_ = polynominal(w, x, d)
error = np.sum((y - y_) ** 2) / len(y_) + lam * np.sum(np.abs(w))
return error
先程と同様に minimize 関数で,ラッソ回帰の目的関数を最小化する重み$w$を算出します. このとき,次数$d=9$,正則化の係数$\lambda=1$に設定しています.
d = 9 # 次数
lam = 1 # 正則化項の重み
w_init = np.ones(d+1)
result = minimize(lasso, w_init, args=(sample[0], sample[1], d, lam), method="powell")
w = result.x
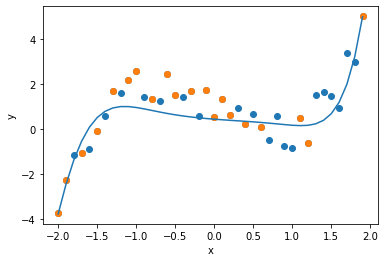
算出された重み$w$を用いて,回帰式をグラフで表します. オーバーフィッティングが回避され,全体の傾向を近似した回帰式が導出されていることが確認できます.
plt.scatter(data[0], data[1] )
plt.scatter(sample[0], sample[1])
plt.plot(data[0], polynominal(w, data[0], d))
plt.xlabel("x")
plt.ylabel("y")
課題
$x^3 - 3x + 3$に従った40点を生成し,そこからランダムに20点を抽出する. この20点をラッソ回帰で学習した回帰式を求めてください. このとき,回帰式は9次の多項式基底とします.
# 40点を生成
x = np.arange(-2, 2, 0.1)
y = x ** 3 - 3 * x + 3
r = np.random.rand(len(y)) * 2 # 乱数を生成
y = y + r # 乱数を加算
data = np.stack([x, y])
# 20点をランダム抽出
sample = np.array(random.sample(list(data.transpose()), 20)).transpose()
課題を完成させたら,chapter6.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定