回帰③・基底関数

基底関数

これまでは回帰式として線形関数（一次式）を採用してきました．

$$f(x) = w_0 + w_1 x $$

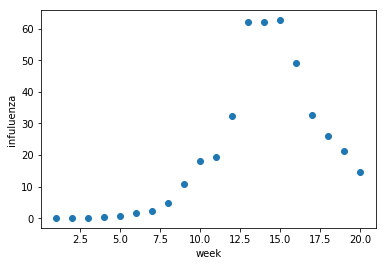
しかし，下記のようなデータを対象とする場合は，直線ではなく曲線を用いた方が，傾向を正しく表現できそうです． このデータは，愛知県衛生研究所が公開しているインフルエンザの発症数です． 変数$x$は 経過週 ，変数$y$は インフルエンザの報告数（定点当たり） を表しています．

x = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]) #週
y = np.array([0.26,0.25,0.19,0.34,0.89,1.78,2.51,4.81,10.97,18.02,19.28,32.42,62.12,62.18,62.60,49.18,32.57,25.93,21.17,14.68]) #報告数

このような場合は，基底関数 を利用します． 線形関数の$x$を，任意の$\phi(x)$という基底関数に置き換えるという方法です． 基底関数には，どんな関数を用いても良いのですが，よく用いられるのは， 多項式基底 や ガウス基底 と呼ばれる関数です． 今回は，これら 基底関数 を利用した回帰について学びます．

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter5 とします． ここでは，numpy と matplotlib.pyplotに加え， 最適化処理のためのScipyをインポートします．

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

多項式基底

多項式基底は下記の式で表されます． ここで，$i$は組み合わせる基底関数の番号を表します．

$$ \phi_i(x) = x^i $$

回帰式

4つの基底関数を組み合わせると，回帰式は下記のように表されます （2つの基底関数を組み合わせた場合は線形関数と一致する）． この回帰式では，$w_0$，$w_1$，$w_2$，$w_3$の4つのパラメータの最適値を求めることが目的です．

$$ f(x) = w_0 \cdot \phi_0(x) + w_1 \cdot \phi_1(x) + w_2 \cdot \phi_2(x) + w_3 \cdot \phi_3(x) $$

$$ = w_0 \cdot x^0 + w_1 \cdot x^1 + w_2 \cdot x^2 + w_3 \cdot x^3 $$

$$ = w_0 + w_1 \cdot x + w_2 \cdot x^2 + w_3 \cdot x^3 $$

この回帰式を関数 fx として定義しておきます．

def fx(w, x): # 回帰式の関数定義
  y_ = w[0]  + w[1] * x + w[2] * x**2  + w[3] * x**3
  return y_

目的関数

目的関数$E$は，これまでと同じ2乗誤差で与えます．

$$E=\sum_{n=0}^{N-1} (y_n - f(x_n))^2$$

この目的関数を関数 gx として定義しておきます．

def gx(w, x, y): # 目的関数（2乗誤差）の関数定義
  y_ = fx(w, x)
  e = np.sum((y - y_) ** 2)
  return e

数値解の導出

数値解の導出には， SciPy を利用します． 同ライブラリの minimize 関数は，指定した関数を最小化するようなパラメータを導出してくれます． 引数には，目的関数 gx ，パラメータの初期値 w_init ， 最適化の対象とならないパラメータ (x, y) ， 最適化アルゴリズム powell を指定します．

[In:]

w_init = np.array([0, 0, 0, 0]) # パラメータの初期値
result = minimize(gx, w_init, args=(x, y), method="powell") # Powell法で最適化
print(result.x) # 導出されたパラメータ

[Out:]

[ 20.22701023 -14.62576848   2.32622593  -0.08134343]

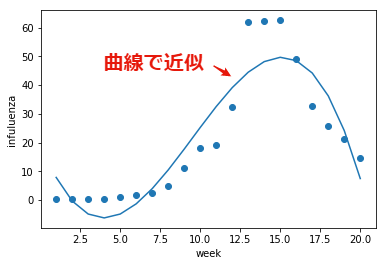
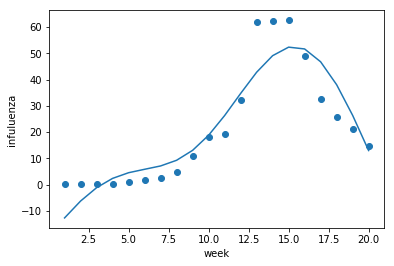
この結果，$w_0 \simeq 20.23$，$w_1 \simeq -14.63$，$w_2 \simeq 2.32$，$w_3 \simeq 0.08$であることがわかりました． この値を基に回帰式をグラフ化すると，曲線を利用して対象のデータを近似していることがわかります．

plt.scatter(x, y)
plt.plot(x, fx(result.x, x))
plt.xlabel("week")
plt.ylabel("infuluenza")

ガウス基底

ガウス基底は下記の式で表されます． ここで，$i$は組み合わせる基底関数の番号を表します． 関数の中心位置（平均）を表す$\mu_i$，関数の広がり（標準偏差）を表す$s$は，事前に適切な値に設定します． また，$s$は全ての関数で共通とします．

$$ \phi_i(x) = \exp \left( - \frac{ (x - \mu_i)^2}{2s^2} \right) $$

ガウス基底を関数 gauss として定義しておきます．

def gauss(x, mu, s):
  g = np.exp( -(x - mu) ** 2 / (2 * s**2))
  return g

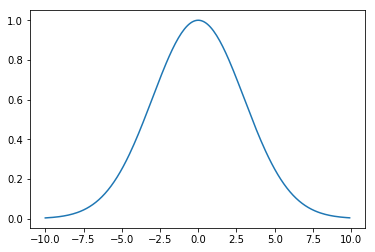
ガウス基底の形状を確認しましょう． $\mu=0$，$s=3$のグラフを描いてみます． ガウス基底は上に凸の分布であり，正規分布（ガウス分布）と同じ形状であることが分かります． 正規分布の正規化（面積の総和を1にする）のための係数を取り除いた式がガウス基底です．

x_ = np.arange(-10, 10, 0.1)
y_ = gauss(x_, 0, 3)
plt.plot(x_, y_)

回帰式

4つの基底関数を組み合わせることにします． このとき，$\phi_0(x)=1$とするため，実際は残りの3つのガウス基底を組み合わせることになります．

$$ f(x) = w_0 \cdot 1 + w_1 \cdot \phi_1(x) + w_2 \cdot \phi_2(x) + w_3 \cdot \phi_3(x) $$

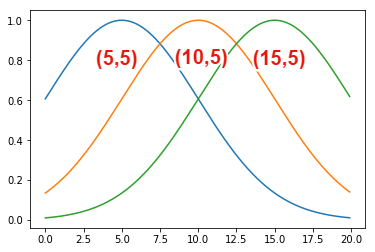
この3つのガウス基底の平均$\mu$と間隔$s$は下記のように設定します．

$$ (\mu_1=5, s_1=5), (\mu_2=10, s_2=5), (\mu_3=15, s_3=5), $$

これは3つのガウス基底を均等な間隔で配置することを意味しています．

この回帰式を関数 fx として定義しておきます．

def fx(w, x): # 回帰式の関数定義
  y_ = w[0]  + w[1] * gauss(x, 5, 5) + w[2] * gauss(x, 10, 5)  + w[3] * gauss(x, 15, 5)
  return y_

目的関数

目的関数$E$は，多項式基底と同じ2乗誤差で与えます．

数値解の導出

多項式基底と同様に SciPy で最適化します．

[In:]

w_init = np.array([0, 0, 0, 0]) # パラメータの初期値
result = minimize(gx, w_init, args=(x, y), method="powell") # Powell法で最適化
print(result.x) # 導出されたパラメータ

[Out:]

[-60.68720705  74.75886194 -44.73746539 130.07080173]

この結果，$w_0 \simeq -60.69$，$w_1 \simeq -74.76$，$w_2 \simeq -44.74$，$w_3 \simeq 130.07$であることがわかりました． この値を基に回帰式をグラフ化すると，多項式基底と同様に曲線で対象のデータを近似していることがわかります．

plt.scatter(x, y)
plt.plot(x, fx(result.x, x))
plt.xlabel("week")
plt.ylabel("infuluenza")

課題

下記のデータの回帰式を求めてください． 回帰式は3次の多項式を基底とすること．

# 経過月
x = np.arange(0, 48, 1)

# 株価
y = np.array([8000,10500,10600,11000,12600,14000,12100,10800,9000,7680,8480,9040,10300,11100,11500,16900,18500,18200,26200,27500,41800,64800,49600,47200,50800,56100,74000,86800,82300,83300,66800,75500,71700,79500,84900,117000,111000,94400,93500,87900,82000,88900,86200,87900,86800,75400,87000,90800])

課題を完成させたら，chapter5.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定