回帰②・最急降下法

解析解と数値解

前回は2変数の関係性を表す 回帰式 と， その回帰式の当てはまり具合を評価するための 最小二乗法 について学びました． 回帰式の形を決める傾き $a$ と切片 $b$ の最適値は， numpy の polyfit 関数を利用して求めましたが，どのように最適値を求めているのでしょうか． 今回はその秘密に迫ってみたいと思います．

回帰式のパラメータ（$a$と$b$のこと）を求める方法には２通りあり， 方程式を解くことによって得られる厳密な解を 解析解， 繰り返しの計算によって得られる近似的な解を 数値解 と呼びます． 特定の処理を繰り返すことが得意なコンピュータでは， 後者の 数値解 を求める方法が良く用いられます． ここでは，数値解を求めるための最もシンプルな方法である 最急降下法（Gradient Descent Method） について学びます．

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter4 とします． 前回と同様に，numpy と matplotlib.pyplot を導入します．

import numpy as np
import matplotlib.pyplot as plt

最急降下法

最急降下法は，目的関数（2乗誤差）の傾き（勾配）を求め， 誤差が小さくなる方向へパラメータを更新するという手法です． 理解するためには 微分 が必要となりますが， 決して難しい計算ではないため，焦らず落ち着いて考えていきましょう．

データ

対象とするデータは前回と同じ，気温 と アイスクリーム のデータを用います． いずれも，numpyのndarray型でリストを作成しておきます．

x = np.array([12, 20, 13, 24, 28, 30, 31, 24, 18, 33]) # 気温
y = np.array([21, 35, 22, 29, 37, 46, 50, 27, 25, 49]) # アイスクリームの売上

回帰式

今回も，線形回帰（一次式）を考えますが， 回帰式は下記のように，一般化した表現で表すことにします（$a$を$w_1$，$b$を$w_0$に置き換えた）． この$w_0$と$w_1$の最適値を求めることが目的です．

$$f(x_n) = w_0 + w_1 x_n $$

目的関数

目的関数$E$を下記のように定義します． $N$はデータの長さを表しています（ここでは，$N=10$）． $y_n - f(x_n)$は誤差であり，その2乗を計算していることが分かります． $1 / 2$が係数となっていますが，これは後ほどの微分計算で役立ちます（得られる結果に影響はない）．

$$E=\frac{1}{2} \sum_{n=0}^{N-1} (y_n - f(x_n))^2$$

式中の$f(x)$を展開すると下記のようになります．

$$E=\frac{1}{2} \sum_{n=0}^{N-1} (y_n - w_0 - w_1 x_n)^2$$

この目的関数が最小となったとき，$w_0$と$w_1$は最適値とみなします．

目的関数とパラメータの関係

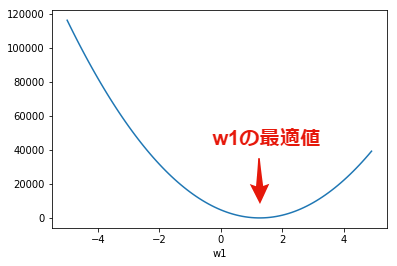
では，この$E$と$w_0$と$w_1$の関係をグラフ化してみましょう． 同時に２つのパラメータ（$w_0$と$w_1$）を考えると難しいため， まずは$w_0=2.52$を固定して考えます（2.52は前回求めた最適値）． $w_1$を-5から5まで変化させたときの，目的関数の値は下記のグラフとなります． グラフは下に凸のお椀型の形状をしており， 誤差が最小となる$w_1 \simeq 1.36$が最適値となることが分かります．

x_ = np.arange(-5, 5, 0.1) # w1の変化
y_ = [] # 空のリスト
w0 = 2.52 # w0を固定

for w1 in x_:
    E = np.sum(1/2 * (y - w0 - w1 * x) ** 2) # 2乗誤差
    y_.append(E) # リストに要素を追加

plt.plot(x_, y_)
plt.xlabel("w1") # 水平軸のラベル

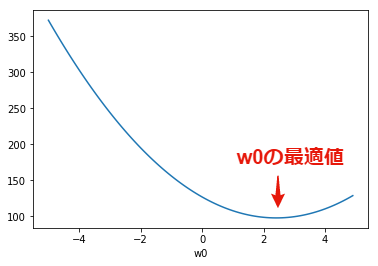
同様に，$w_1=1.36$に固定して考えます（1.36は前回求めた最適値）． $w_0$を-5から5まで変化させたときの，目的関数の値は下記のグラフとなります． グラフは下に凸のお椀型の形状をしており， 誤差が最小となる$w_0 \simeq 2.52$が最適値となることが分かります．

x_ = np.arange(-5, 5, 0.1) # w0の変化
y_ = [] # 空のリスト
w1 = 1.36 # w1を固定

for w0 in x_:
    E = np.sum(1/2 * (y - w0 - w1 * x) ** 2) # 2乗誤差
    y_.append(E) # リストに要素を追加

plt.plot(x_, y_)
plt.xlabel("w0") # 水平軸のラベル  

学習則

目的関数$E$は，$w_0$と$w_1$に対して，下に凸のお椀型の形状をしていることがわかりました． 最急降下法では，初期値として$w_0$と$w_1$に適当な値を設定し，坂を下る方向に$w_0$と$w_1$を更新することで最適値を探します． このためには，誤差$E$を$w_0$と$w_1$で偏微分し，接線の傾きを計算します．

$$ \frac{\partial E}{\partial w_0} = 2 \cdot \frac{1}{2} \sum^{N-1}_{n=0} (y_n - w_0 -w_1 x_n) \cdot -1 $$ $$ = -\sum^{N-1}_{n=0} (y_n - w_0 -w_1 x_n) $$

$$ \frac{\partial E}{\partial w_1} = 2 \cdot \frac{1}{2} \sum^{N-1}_{n=0} (y_n - w_0 -w_1 x_n) \cdot -x_n $$ $$ = -\sum^{N-1}_{n=0} (y_n - w_0 -w_1 x_n) x_n $$

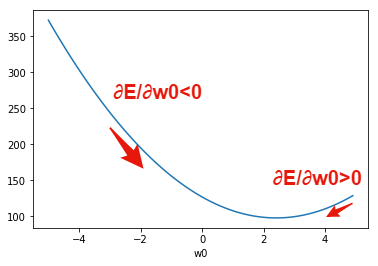
接線の傾き$\frac{\partial E}{\partial w_0} < 0$のときは， $w_0$を増加させることで，より誤差を小さくすることができます． 逆に，接線の傾き$\frac{\partial E}{\partial w_0} > 0$のときは， $w_0$を減少させることで，より誤差を小さくすることができます．

この$w_0$と$w_1$の更新を下記の式で与えます． この式は 学習則 と呼ばれます． ここで，$\alpha$は 学習率 と呼ばれ，$w_0$と$w_1$の更新の幅を調整するパラメータです． 大きな値を設定すると収束は早くなりますが，結果に大きな誤差が含まれる可能性が高くなります． 一方，小さな値を設定すると，結果に含まれる誤差は小さくなりますが，収束が遅くなってしまいます． このため，収束速度と誤差のバランスを調整した適切な値を設定する必要があります．

$$ w_0' = w_0 - \alpha \frac{\partial E}{\partial w_0} $$

$$ w_1' = w_1 - \alpha \frac{\partial E}{\partial w_1} $$

数値解の導出

それでは，最急降下法を利用して，$w_0$と$w_1$の数値解を求めてみましょう． パラメータの初期値は$w_0=0$，$w_1=0$，学習率は$\alpha=0.0001$とします． パラメータの更新を10万回繰り返した後に，$w_0$，$w_1$の値と，目的関数の値を出力しています． この結果，$w_0 \simeq 2.52$，$w_1 \simeq 1.36$となり，前回にpolyfit関数で求めた値とほぼ一致していることが分かります．

[In:]

w0 = 0 # w0の初期値
w1 = 0 # w1の初期値
alpha = 0.0001

for i in range(100000):
    g0 = -1 * np.sum(y - w0 - w1 * x) # w0の偏微分
    g1 = -1 * np.sum((y - w0 - w1 * x) * x) # w1の偏微分
    w0 = w0 - alpha * g0 # w0の更新
    w1 = w1 - alpha * g1 # w1の更新

E = np.sum(1/2 * (y - w0 - w1 * x) ** 2) # 目的関数の計算
print(w0)
print(w1)
print(E)

[Out:]

2.518733969947924
1.3554170191576644
97.5964381152417

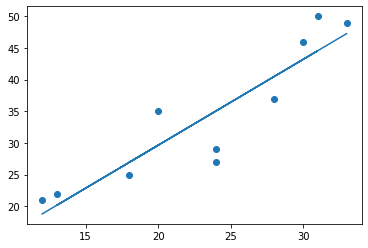
最後に導出した$w_0$と$w_1$を利用して回帰式をグラフで描画してみます． 前回と同様の回帰式が描けていることがわかります．

fx = w0 + w1 * x
plt.scatter(x, y)
plt.plot(x, fx)

課題

下記のデータの回帰式を最急降下法で求めてください． ただし，$\alpha=0.00001$，繰り返し回数を100万回とすること．

x = np.array([50, 55, 62, 68, 75, 88, 90, 92, 94, 99])
y = np.array([89, 86, 77, 80, 68, 73, 58, 62, 58, 60])

課題を完成させたら，chapter4.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定