回帰①・線形回帰

機械学習の分類

機械学習は大別して３種類あるとされています．

• 教師あり学習（Supervised Learning）
• 教師なし学習（Unsupervised Learning）
• 強化学習（Reinforcement Learning）

教師あり学習 は，未知のデータに対する分類や予測などの問題において， 過去のデータに対して正解（教師）が事前に与えられている学習方法です． 過去のデータの正解が分かっているため，未知のデータに対しては， 過去のデータとの類似性を基に判断することになります． 例えば，特定の顔写真をデータとして学習させると， 未知の写真に対して，一致するかどうかを判定できるようになります．

教師なし学習 は，正解（教師）が事前に与えられない学習方法です（もしくは明確な正解が存在しない）． よって，分類や予想ではなく，データに潜む傾向や特徴を抽出する目的で用いられます． データマイニングと呼ばれる研究分野にも関係が深いです． 例えば，POS（Point of Sales）データなどから， 商品売上の傾向（「おむつとビール」が有名）を明らかにすることが出来ます．

強化学習 は，ロボット（エージェント）が，環境や経験からの情報を基に， 最適な行動ルールを獲得するための学習方法です． 一般には，マルコフ決定過程（Marcov Decision Process）というプロセスに従って学習は進行します． 例えば，自動運転自動車が，他の車両や歩行者を回避するための運転操作を， 自動的に獲得することができます．

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter3 とします． グラフを作成するために，Matplotlibといライブラリを用います． ライブラリを導入するには import matplotlib as pltとします． ここで，as plt は，ライブラリのエイリアス（別名）として， plt を用いることを意味しています（省略も可能です）．

import matplotlib.pyplot as plt

同様に，高度な算術計算をサポートするnumpy というライブラリを用います． ここでは，import numpy as npでライブラリを導入し， np というエイリアス（別名）をつけています．

import numpy as np

回帰

今回は，教師あり学習に分類される回帰 に焦点を当てます． 回帰分析 とは，2変数（もしくはそれ以上）の関係性を 数式 で表すという手法です． 例えば，過去の「気温」と「アイスクリームの売上」のデータを基に， それらの関係性を表す数式を導き，将来の売上を予測することができます．

ここでは，下記に示す10日間分のデータで考えましょう． 変数xは気温，変数yはアイスクリームの売上を表しています．

x = [12, 20, 13, 24, 28, 30, 31, 24, 18, 33] # 気温
y = [21, 35, 22, 29, 37, 46, 50, 27, 25, 49] # アイスクリームの売上

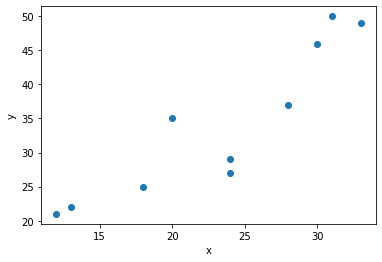
このデータを散布図にしてみます． 横軸を気温，縦軸を売上として，散布図を描くには，plt.scatter(x, y)とします．

plt.scatter(x, y) # 散布図を描く
plt.xlabel("x")
plt.ylabel("y")

グラフから全体の傾向が分かりますね． 予想していたとは思いますが，気温が高いほど，アイスクリームの売上は伸びそうです． この傾向を，客観的な 数式 で表現する方法が回帰分析です．

線形回帰

それでは，売上の傾向を表す数式を求めてみましょう． ここでは，最もシンプルな 線形回帰 で考えます． 線形回帰は下記の一次式（ 回帰式 ）で与えられます．

$$y = a \cdot x + b $$

式中の $a$は傾き，$b$は切片ですよね（中学で学んだはず）． この$a$と$b$を適切に調整してあげれば，売上の傾向を直線で表現できそうです． まずは，$a=1$，$b=10$で考えてみることにします．

$$y = 1 \cdot x + 10 $$

上記の式をグラフにするために，回帰式の関係を満たす$x$と$y$のリストを作成します． Numpyのarange 関数は，指定の条件でリスト（正確にはndarray型）を作成します． np.arange(10, 40, 1)は，10から39まで，間隔（交差）を1とした，リストを作成するという意味です．

[In:]

x2 = np.arange(10, 40, 1) # 10..39のリスト（正確にはndarray型）を作成
y2 = 1 * x2 + 10 # 式を計算
print(x2)
print(y2)

[Out:]

array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26,
       27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39])
array([20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36,
       37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49])

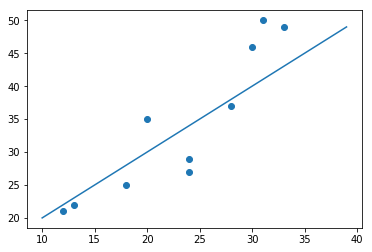
それでは，回帰式の折れ線グラフを描きましょう． 折れ線グラフを描くには，plt.plot(x2, y2)とします． 適当に$a$と$b$を設定しましたが，ある程度は全体の傾向を表現できているようです． データの傾向を近似した最適なaとbを求めるにはどうしたら良いでしょうか．

plt.scatter(x, y)
plt.plot(x2, y2)

最小二乗法

最適な$a$と$b$を求める方法の一つが 最小二乗法 です． これは，データと求める回帰式の 誤差 を最小にするという手法です．

誤差 を定義するために， 気温$x$に対する，式で求めた予測の売上$f(x)$を求めます． このとき，気温と売上のデータは，リストからndarray型に変換しておきます．

$$f(x) = 1 \cdot x + 10 $$

[In:]

x = np.array(x) #気温をndarray型に変換
y = np.array(y) #売上をndarray型に変換
fx = 1 * x + 10
print(x)
print(y)
print(fx)

[Out:]

array([12, 20, 13, 24, 28, 30, 31, 24, 18, 33])
array([21, 35, 22, 29, 37, 46, 50, 27, 25, 49])
array([22, 30, 23, 34, 38, 40, 41, 34, 28, 43])

これを散布図として描きます． このとき，$y$と$f(x)$の差を 誤差 と定義します． この 誤差 が小さければ，回帰式は過去のデータを上手く近似していることになります．

plt.scatter(x, y)
plt.scatter(x, fx)

それでは，誤差 を求めてみます． そのまま$y - f(x)$を計算すると，正と負の値が混在することになり，扱いが難しくなります． そこで，誤差の二乗 を求め，この総和を計算します（np.sum 関数はリストの総和を返す）． 計算結果は 264 となり，この値がデータ全体に対する誤差を表しています． この値を最小にするような，$a$と$b$を求めるのが最小二乗法です．

[In:]

y - fx
(y - fx) ** 2
np.sum( (y-fx) ** 2)

[Out:]

array([-1,  5, -1, -5, -1,  6,  9, -7, -3,  6])
array([ 1, 25,  1, 25,  1, 36, 81, 49,  9, 36])
264

polyfit関数

それでは，numpy の polyfit 関数を利用して，最適な$a$と$b$の値を求めてみましょう（ パラメータ と呼ぶこともあります）． np.polyfit(x, y, 1)は，$x$と$y$を近似する，$1$次式の$a$と$b$を求めます． ここでは，$a \simeq 1.36$，$b \simeq 2.52$となりました． 誤差の二乗を計算すると約 195 となり，先程求めた 264 より小さな値になっていることがわかります．

$$f(x) \simeq 1.36 \cdot x + 2.52 $$

[In:]

(a, b) = np.polyfit(x, y, 1)
print(a)
print(b)

[Out:]

1.3553936450111312
2.5193280712406407

[In:]

fx = a * x + b
print(fx)
np.sum( (y - fx) ** 2)

[Out:]

array([18.78405181, 29.62720097, 20.13944546, 35.04877555, 40.47035013,
       43.18113742, 44.53653107, 35.04877555, 26.91641368, 47.24731836])
195.19287593604543

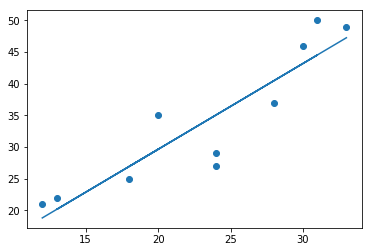
最後に求めた式を折れ線グラフで描画してみましょう． 先程よりも誤差が小さく，データ全体の傾向を近似出来ていることがわかります．

plt.scatter(x, y)
plt.plot(x, fx)

課題

下記のデータの線形回帰を求めてください． 求めた回帰式はグラフで描画すること．

x = [50, 55, 62, 68, 75, 88, 90, 92, 94, 99]
y = [89, 86, 77, 80, 68, 73, 58, 62, 58, 60]

課題を完成させたら，chapter3.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定