Kaggle②・コンペに挑戦しよう！

ノートブックの作成

Colabにアクセスし，新規にノートブックを作成してください． ノートブックのタイトルは chapter15 とします．

パラメータの最適化

機械学習モデルの精度を向上させるには，パラメータの最適化（チューニング）が欠かせません． 例えば，決定木では，分割基準（gini or entropy），木の最大の深さ（max_depth）， 分割可能な最小ノード数（min_samples_split）などが挙げられます． これらのパラメータは ハイパーパラメータ と呼ばれ， 最適化することで最大のパフォーマンスを発揮することができます． ここでは，ハイパーパラメータの 自動最適化フレームワークであるOptunaを取り上げます． このフレームワークは，日本企業のPreferred Networksが開発しており， 国内外の様々なプロジェクトで導入されています．

Optunaをインストールして，必要なライブラリを導入します． ここで，mplot3dは， 散布図や曲面などを3次元空間にプロットするためのライブラリです．

!pip install optuna

import optuna
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D

Optunaで最適化する関数$f(x,y)$を定義します． この関数を最小化するパラメータ$x$と$y$を探索します．

$$ f(x, y) = x^2 + y^2 $$

# 関数f(x, y)を定義
def f(x, y):
  return x**2 + y**2

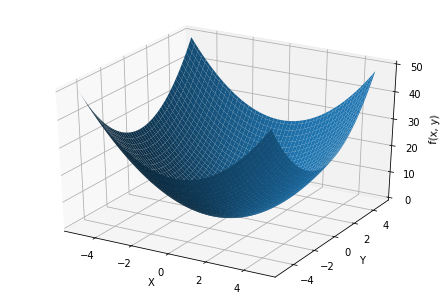
関数$f(x)$を3次元空間にプロットします． 図から分かるように，この問題の最適解は$x=0$，$y=0$です．

# 関数f(x, y)の可視化
x_list = np.arange(-5, 5, 0.1)
y_list = np.arange(-5, 5, 0.1)

X, Y = np.meshgrid(x_list, y_list)
Z =  f(X, Y)

fig = plt.figure()
ax = Axes3D(fig)
ax.plot_surface(X, Y, Z)
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("f(x, y)")

それでは，Optunaの目的関数を定義しましょう． このとき，Trialクラスを利用して，探索するパラメータの空間を指定します． ここでは，$x$の探索空間は-5から5，同様に$y$の探索空間も-5から5に設定します． 整数を探索するときはsuggest_int，実数を探索するときはsuggest_floatなど， 探索空間の種類に応じて異なる関数を用います．

# 目的関数を定義
def objective(trial):
    x = trial.suggest_int("x", -5, 5) #-5〜5までを探索
    y = trial.suggest_int("y", -5, 5) #-5〜5までを探索
    return f(x, y)

目的関数を最小化するパラメータを探索します． 探索回数n_trialsは100に設定しました．

# 最適なパラメータを探索
study = optuna.create_study(direction="minimize") # 最適化処理を管理するstudyオブジェクト
study.optimize(objective, n_trials=100)

[I 2021-09-27 07:09:08,706] A new study created in memory with name: no-name-9c66fd90-bcc3-45ed-9d80-2d8742dcf962
[I 2021-09-27 07:09:08,712] Trial 0 finished with value: 2.0 and parameters: {'x': -1, 'y': 1}. Best is trial 0 with value: 2.0.
[I 2021-09-27 07:09:08,716] Trial 1 finished with value: 17.0 and parameters: {'x': 4, 'y': -1}. Best is trial 0 with value: 2.0.
[I 2021-09-27 07:09:08,720] Trial 2 finished with value: 20.0 and parameters: {'x': 4, 'y': 2}. Best is trial 0 with value: 2.0.
[I 2021-09-27 07:09:08,724] Trial 3 finished with value: 20.0 and parameters: {'x': -4, 'y': -2}. Best is trial 0 with value: 2.0.
[I 2021-09-27 07:09:08,729] Trial 4 finished with value: 41.0 and parameters: {'x': -5, 'y': -4}. Best is trial 0 with value: 2.0.

探索の結果，最適なパラメータである$x=0$，$y=0$が発見されました． このように，機械学習のモデルに合わせて最適なパラメータを探索することで， パフォーマンスを改善させることができます．

# 最適なパラメータ
print(study.best_params)

{'x': 0, 'y': 0}

コンペの紹介

Kaggle

Kaggleで公開されている初学者向けのコンペを紹介します.

スパムメールの分類（Just the Basics - Strata 2013 After-party）

通常のメールとスパムメールを分類する問題です． メール・コーパスによる100種類の特徴量で構成されています（データには属性名が含まれていないので注意）．

https://www.kaggle.com/c/just-the-basics-the-after-party/

手書き数字の分類（Digit Recognizer）

手書き数字（$0〜9$）を分類する問題です． データセットはMNISTとして広く知られています． $28 \times 28$ピクセルの画素値（$0〜255$）がデータとして提供されます．

https://www.kaggle.com/c/digit-recognizer/data?select=train.csv

タクシー料金の予測（New York City Taxi Fare Prediction）

ニューヨークのタクシー料金を回帰アルゴリズムで予測します． データは乗降車の時刻や緯度経度など8属性で構成されています． 回帰問題であることから評価には平均2乗誤差（Root Mean Square Error: RMSE）が用いられます．

https://www.kaggle.com/c/new-york-city-taxi-fare-prediction

住宅価格の予測（House Prices - Advanced Regression Techniques）

住宅価格を回帰アルゴリズムで予測することを目的とします． データは敷地面積（LotArea），建築年（yearBuilt）などの81属性で構成されています． 評価には平均2乗誤差（Root Mean Square Error: RMSE）が用いられます．

https://www.kaggle.com/c/house-prices-advanced-regression-techniques/

SIGNATE

SIGNATEで公開されている初学者向けのコンペを紹介します． SIGNATEは国内企業が主催しているコンペであり，AIやビッグデータを利用した課題解決を目的としています． 賞金が懸けられたコンペに加え，初心者用の練習問題や学習教材も揃っています．

天秤のバランス分類

天秤の左右の重量と距離から，天秤のバランス（左，平衡，右）を分類する問題です． 説明変数が4属性しかなく，初心者が挑戦するには最適です．

https://signate.jp/competitions/130

都市サイクルの燃料消費量予測

重量，加速，車名などから，自動車の燃費（燃料消費量）を予測（回帰）する問題です． 電気自動車や自動運転など注目される分野の問題の一つです．

https://signate.jp/competitions/129

学習アルゴリズムの紹介

コンペでよく使用される学習アルゴリズムを紹介します．

バギング

バギング を利用したアルゴリズムに RandomForest があります． バギングとは，独立した複数の学習器を作成し，それらの多数決で解を定める方法です．

RandomForest

https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html

ブースティング

ブースティング を利用したアルゴリズムには， XGBoost，LightGBM，CatBoost などがあります（参考: 勾配ブースティング決定木（XGBoost, LightGBM, CatBoost）を実装してみた」）． ブースティングは，バギングとは異なり独立した学習器を作成するのではなく， ある学習器から，その弱点を補う学習器を生成する，ということを繰り返し， それらの多数決で解を定める方法です．

XGBoost

https://github.com/dmlc/xgboost/

LightGBM

https://github.com/microsoft/LightGBM/

CatBoost

https://catboost.ai/

課題

自由にコンペを選び，その結果を報告してください． 課題を完成させたら，chapter15.ipynb を保存し， 共有用のリンク と ノートブック（.ipynb） をダウンロードして提出してください． このとき，必ず事前に下記の設定を行ってから提出してください．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定
• 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定