混合ガウスモデル
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter13 とします. また,numpy,matplotlib.pyplot,scikit-learn,SciPyを導入しておいてください.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
from scipy.stats import norm
ガウス分布(正規分布)
ガウス分布(正規分布)は,ドイツの数学者のガウスに由来する確率・統計において最重要な確率分布の一つです. 自然界や社会の様々な現象を表現するモデルとして知られています. Pythonでは,Numpyを利用して,正規分布に従う乱数を生成することが可能です.
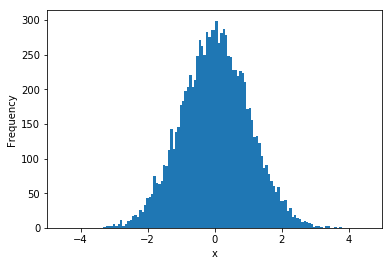
例えば,平均0,標準偏差1の正規分布に従う乱数を生成してみます. 生成した乱数のヒストグラム(度数)は下図のようになります. このヒストグラムからも分かるように,正規分布には下記の特徴があります.
- 平均値がピークとなる
- 平均値を中心として左右対称
- 標準偏差が小さいと尖った形状,大きいと平らな形状
x = np.random.normal(0, 1, 10000) # 10000の乱数を生成
plt.hist(x, bins=100) # 階級数を100に設定したヒストグラム
plt.xlim(-5, 5)
plt.xlabel("x")
plt.ylabel("Frequency")
正規分布に従う特徴量の一つに人間の身長があります. 例えば,日本人男性の平均は167.7cm,標準偏差は6.6cm, また,アメリカ人男性の平均は178.4cmで,標準偏差は7.6cmとされています. それでは,この特徴量を利用して日本人男性とアメリカ人男性の正規分布に従う乱数を生成しましょう. そして,これを重ね合わせてしまいます.
x1 = np.random.normal(167.7, 6.6, 10000)
x2 = np.random.normal(178.4, 7.6, 10000)
x = np.concatenate((x1, x2)) # 結合(重ね合わせ)
plt.hist(x, bins=100)
plt.xlabel("x")
plt.ylabel("Frequency")
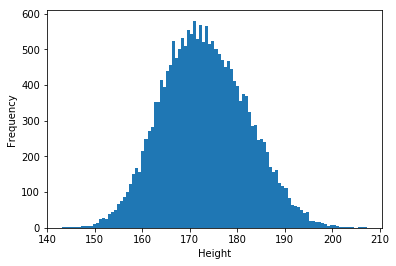
結合された乱数のヒストグラムは下記のようになります. このように複数の正規分布に従う乱数を重ね合わせることで, 多彩な分布を表現することが可能になります. この正規分布を重ね合わせた表現を 混合ガウスモデル(Gaussian Mixture Model) と呼びます. 一方で,重ね合わせた分布からは,元の正規分布の特徴量を得ることは難しくなります. これを得るには EMアルゴリズム と呼ばれる手法が用いられます(詳細は割愛).
scikit-learnで混合ガウスモデル
それでは,scikit-learnを利用して 混合ガウスモデル(Gaussian Mixture Model) の特徴量を推定してみましょう.
まずは,対象のデータをreshapeで2次元配列に変換します(scikit-learnの制限のため).
[In:]
x = np.array(x).reshape(-1, 1)
print(x)
[Out:]
[[162.08389117]
[170.77306785]
[165.28550483]
...
[175.53732234]
[178.69420996]
[177.08352499]]
次に,scikit-learnのGaussianMixtureを利用して特徴量を推定します. このとき,重ね合わせた元の正規分布の 数 と 分散 を指定します. ここでは,各次元の分散が共通である2つの正規分布が重なっているとします(今回のデータは身長のみの1次元).
gmm = GaussianMixture(
n_components=2, # 重ね合わせた分布数
covariance_type="spherical" # 分散は共通(球状)
).fit(x)
推定された 重み,平均,標準偏差を調べてみましょう. 推定された日本人男性の平均は167.4cm,標準偏差は6.4cm,また, 推定されたアメリカ人男性の平均は179.7cm,標準偏差は6.9cmです. かなり高い精度で推定されていることが分かります. また,重みは2つの分布を混合した割合を意味しており, 推定された重みは0.53:0.46となりました. 今回は0.5:0.5で混合したため,これもほぼ一致していることが分かります.
[In:]
weight = gmm.weights_ #重み(足すと1になる)
mean = gmm.means_ #平均
sd = np.sqrt(gmm.covariances_) #標準偏差
print(weight)
print(mean)
print(sd)
[Out:]
[0.46127772 0.53872228] #重み(足すと1になる)
[[179.65302075] [167.4491238 ]] #平均
[6.92751809 6.35107582] #標準偏差
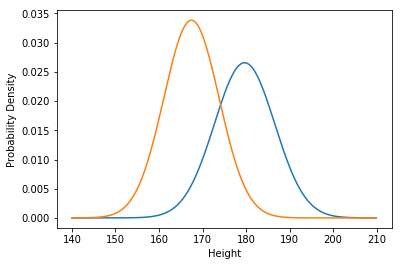
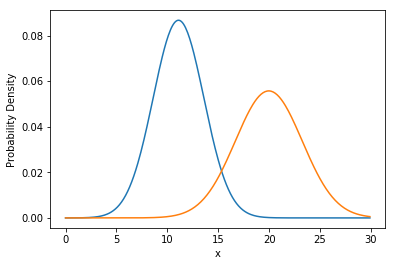
推定された特徴量を用いて,正規分布を描いてみましょう.
正規分布の確率密度を求めるには norm.pdf を利用します.
x_ = np.arange(140, 210, 0.1)
y1 = weight[0] * norm.pdf(x_, mean[0], sd[0])
y2 = weight[1] * norm.pdf(x_,mean[1], sd[1])
plt.plot(x_, y1)
plt.plot(x_, y2)
plt.xlabel("Height")
plt.ylabel("Probability Density")
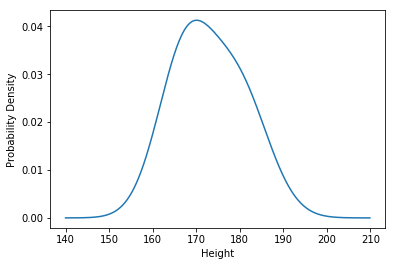
この2つの正規分布を重ねると,元の分布の形状とほぼ一致した確率分布を得ることができます.
y3 = y1 + y2
plt.plot(x_, y3)
plt.xlabel("Height")
plt.ylabel("Probability Density")
さて,今回の混合ガウスモデルは,前回の k平均法 と同じように,
クラスタリングの手法としても用いることができます.
例えば,165cmの男性がどちらの分布(クラスタ)に属するかを predict で判定すると,
日本人の分布に属しているという結果になりました.
同様に,185cmの男性は,アメリカ人の分布に属しているという結果になりました.
[In:]
sample1 = np.array([[165]]) # 165cm
sample2 = np.array([[185]]) # 185cm
result1 = gmm.predict(sample1)
result2 = gmm.predict(sample2)
print(result1) # 日本人
print(result2) # アメリカ人
[Out:]
[1]
[0]
課題
下記のデータから元の正規分布の特徴量を推定しなさい. ただし,正規分布の数は2,また,分散は共通とすること.
x = np.array([14.25503594, 8.83020581, 10.45406782, 12.53819445, 7.86459267,
8.03801485, 11.31295349, 10.09167258, 12.87803092, 14.48622644,
11.99081559, 9.63743057, 10.77132259, 10.50821578, 12.2923627 ,
6.83922144, 11.59345268, 8.38998967, 11.77040723, 8.50230634,
7.3762556 , 11.11177995, 13.57393876, 14.39937259, 8.92640252,
12.62335089, 10.04121407, 11.20886925, 10.53488673, 7.57188571,
19.20054947, 20.67642748, 17.81617885, 24.66817129, 20.9813163 ,
21.92106427, 19.31876107, 17.31019546, 16.69085822, 14.48237459,
20.35137646, 20.19614246, 16.47291945, 18.87417032, 24.24447717,
26.12173461, 27.47509222, 19.05972395, 18.82537232, 18.87784878,
20.60160528, 14.17361497, 18.01530688, 21.87758915, 16.012469 ,
19.69841929, 22.10291163, 15.22297199, 23.14124462, 14.84946092])
課題を完成させたら,chapter13.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定