k平均法
クラスタリング
これまで取り上げた手法は全て 教師あり学習 でした. 今回は,正解(教師)が与えられない 教師なし学習 に注目します. 教師なし学習の一つが クラスタリング と呼ばれる手法です. クラスタリングは,対象データの類似度を基に,グループ(クラスタ)に分けることが目的となります. 分類と混同されがちですが,正解(教師)は存在しないため, 同じクラスタに割り当てられたデータは 似ている とみなすことができますが, その割り当てが 正しい, 正しくない といった判断は出来ないことに注意してください. また,クラスタリングには,階層型手法 と 非階層型手法 に分かれますが, ここでは非階層型手法を取り上げることにします.
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter12 とします. また,numpy,matplotlib.pyplot, scikit-learn,pandas を導入しておいてください.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
import pandas as pd
データの準備
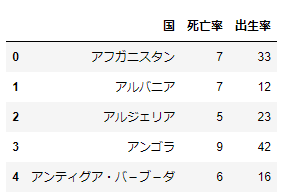
ユニセフ・世界子供白書が公開している人口統計指標のデータを用います. ここでは,世界各国の2016年度の出生率(人口1,000人に対する出生数)と死亡率(人口1,000人に対する死亡数)のデータに着目します. ウェブで公開されているデータを読み込み,pandasのデータフレームを生成します. 例えば,アフガニスタンの死亡率は7,出生率は33であることが分かります.
data = pd.read_csv("http://mukai-lab.info/classes/intelligence_information_system/population2016.csv")
display(data.head()) #最初の5件だけ表示
一方,日本の死亡率は11,出生率は8であり,少子高齢化が進んでいることが読み取れます.
japan = data[data["国"] == "日本"] #日本を表示
display(japan)
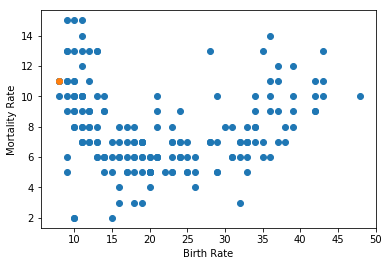
散布図で出生率,死亡率を可視化してみましょう. 他国と比較すると,日本の少子高齢化が極めて大きな問題であることが分かります(この授業の趣旨ではありませんが).
plt.scatter(data["出生率"], data["死亡率"])
plt.scatter(japan["出生率"], japan["死亡率"])
plt.xlabel("Birth Rate")
plt.ylabel("Mortality Rate")
k平均法
今回は,非階層型のクラスタリング手法である k平均法(k-means clustering) を取り上げます( k近傍法 と名前が似ていますが別物です). k平均法では,あらかじめ分割するクラスタ数$k$を決める必要があります. ここでは,$k=3$としましょう.
クラスタの中心ベクトル
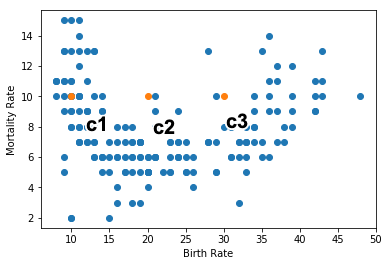
クラスタの位置は,クラスタの中心を表すベクトル ${\bf c} = ( c_1, c_2, c_3 ) $ で表すことにします. ここでは,$c_1 = (10, 10)$,$c_2 = (20, 10)$,$c_3 = (30, 10)$を初期値とします.
[In:]
c1 = np.array([10, 10])
c2 = np.array([20, 10])
c3 = np.array([30, 10])
clusters = np.array([c1, c2, c3])
print(clusters)
[Out:]
[[10 10]
[20 10]
[30 10]]
plt.scatter(data["出生率"],data["死亡率"])
plt.scatter(clusters[:,0], clusters[:,1])
plt.xlabel("Birth Rate")
plt.ylabel("Mortality Rate")
クラスタとの距離
次に,各データがどのクラスタに属するかを調べます. 一般には,各データとクラスタとのユークリッド距離を類似度とみなし, 最も値が小さいクラスタに属すると考えます. ここでは,map 関数と np.linalg.norm 関数を組み合わせて, 各クラスタとの距離を計算しています. 例えば,アフガニスタンの出生率は$7$,死亡率は$33$であるため, クラスタ$c_1$までの距離は下記のように求まります.
$$ \sqrt{(7 - 10)^2 + (33 - 10)^2} = 23.19 $$
[In:]
def distance(data, clusters):
d = []
for index, row in data.iterrows():
x = np.array([row["出生率"], row["死亡率"]])
#clustersの要素cに対するユークリッド距離を計算
value = list(map(lambda c: np.linalg.norm(x - c), clusters))
d.append(value)
return np.array(d)
d = distance(data, clusters) #c1,c2,c3までの距離
print(d[0:5])
[Out:]
[[23.19482701 13.34166406 4.24264069]
[ 3.60555128 8.54400375 18.24828759]
[13.92838828 5.83095189 8.60232527]
[32.01562119 22.02271555 12.04159458]
[ 7.21110255 5.65685425 14.56021978]]
距離が最小となるクラスタの要素番号を調べます. ここは,argmin 関数を用いています. この関数は,配列に記録されている最も小さな値の要素番号を取得します. 例えば,アフガニスタンの場合は,クラスタ$c_3$が最小であり, その要素番号である$2$が取得されます(配列の要素番号は$0$から).
[In:]
def assign(distance):
a = []
for d in distance:
index = np.argmin(d)
a.append(index)
return np.array(a)
a = assign(d)
print(a[0:5])
[Out:]
[2 0 1 2 1]
クラスタの中心ベクトルの更新
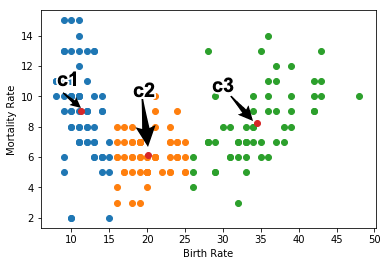
クラスタの中心ベクトルを更新します. 中心ベクトルは,各クラスタに属するデータの 重心(平均) で表されます. この結果,中心ベクトルは,クラスタの中心に移動します. 上記の操作を繰り返し,中心ベクトルの変化がなくなったとき,適したクラスタが得られたとみなします.
[In:]
def updateClusters(data, clusters, a):
updated = []
for i in range(clusters.ndim+1):
index = np.where(a == i)
d = data.iloc[index]
size = np.array(index).size
c = np.array([d["出生率"].sum() / size, d["死亡率"].sum() / size])
updated.append(c)
return np.array(updated)
clusters = updateClusters(data, clusters, a)
print(clusters)
[Out:]
[[11.27941176 9.05882353]
[20.15 6.1 ]
[34.55357143 8.23214286]]
for i in range(clusters.ndim + 1):
index = np.where(a == i)
d = data.iloc[index]
plt.scatter(d["出生率"],d["死亡率"])
plt.scatter(clusters[:,0], clusters[:,1])
plt.xlabel("Birth Rate")
plt.ylabel("Mortality Rate")
上記の操作をクラスタの中心ベクトルが収束するまで繰り返します. 最終的に得られた結果を最適なクラスタリングとみなします.
scikit-learnでK平均法
それでは,機械学習のライブラリである scikit-learn を利用してk平均法によるクラスタリングを実行してみましょう.
k平均法を適用するには cluster.KMeans 関数を用います.
クラスタ数は n_clustersで指定します.
[In:]
km = KMeans(n_clusters=3)
km.fit(data[["出生率", "死亡率"]])
print(km.labels_) # 所属するクラスタ
print(km.cluster_centers_) # クラスタの中心
[Out:]
[1 2 0 1 0 0 2 2 2 0 2 0 0 2 2 2 0 1 0 0 2 0 2 0 2 1 1 0 0 1 2 1 1 2 2 2 1
1 2 1 2 2 2 2 2 1 2 0 0 0 0 0 1 1 2 1 0 2 2 1 1 2 2 1 2 0 0 1 1 0 0 0 2 2
0 0 0 1 2 0 2 0 2 0 0 1 1 0 0 0 2 0 1 1 0 2 2 1 1 0 0 1 2 1 2 0 0 0 2 0 1
0 1 0 2 2 0 1 1 2 0 1 0 1 0 0 0 2 2 2 2 2 2 2 1 2 0 0 1 0 1 2 0 1 2 2 2 1
1 0 1 2 2 1 1 0 1 2 2 0 1 2 2 1 1 0 2 0 0 0 1 2 2 2 1 2 2 0 0 0 0 1 1 1]
[[20.26153846 5.96923077]
[35.03773585 8.41509434]
[11.16666667 9.22727273]]
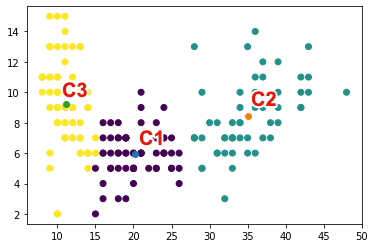
クラスラリングの結果を散布図で可視化してみましょう. 3つのクラスタが構成されていることがわかります.
[In:]
plt.scatter(data["出生率"], data["死亡率"], c=km.labels_)
for x,y in km.cluster_centers_:
plt.scatter(x, y)
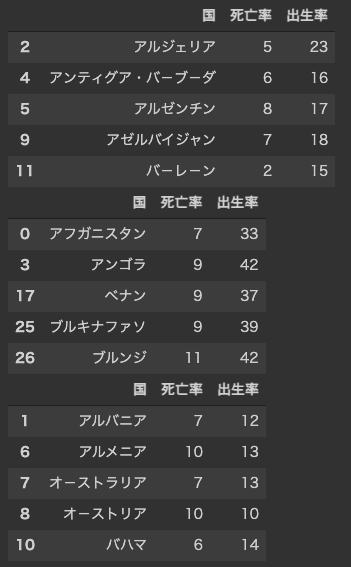
最後に,各クラスタにどのような国が所属しているか確認してみましょう. クラスタ$c_2$は,出生率が高く,死亡率が低いグループです. アフガニスタンなど治安が悪い国や,アンゴラなどの発展途上国が含まれています. クラスタ$c_3$は,出生率が低く,死亡率が高いグループです. オーストラリアやオーストリアなど経済発展が進んだ国が含まれています. クラスタ$c_1$は,その中間であり,アルジェリアやアルゼンチンなどが含まれています.
[In:]
labels = km.labels_
index = np.where(labels==0)
display(data.iloc[index].head())
index = np.where(labels==1)
display(data.iloc[index].head())
index = np.where(labels==2)
display(data.iloc[index].head())
課題
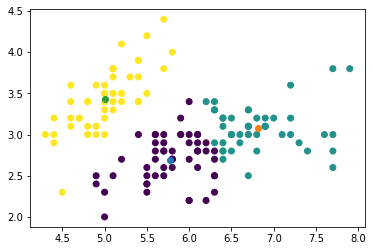
scikit-learnの アヤメの データセットをk平均法でクラスタリングしてください(クラスタ数は3). このとき,がく片の長さ(Sepal Length) とがく片の幅(Sepal Width) のみを対象とすること.
from sklearn.datasets import load_iris
iris = load_iris()
data = pd.DataFrame(iris.data)
data.columns = ["がく片の長さ","がく片の幅","花弁の長さ","花弁の幅"]
課題を完成させたら,chapter12.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定