決定木
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter11 とします.
最初にグラフで日本語表示を可能とするjapanize-matplotlibをインストールします.
!pip install japanize-matplotlib
また,numpy,matplotlib.pyplot ,scikit-learn に加えて, データフレームを処理するための Pandasをインポートします.
import numpy as np
import matplotlib.pyplot as plt
from sklearn import tree
from sklearn.tree import plot_tree
import pandas as pd
import japanize_matplotlib
データの準備
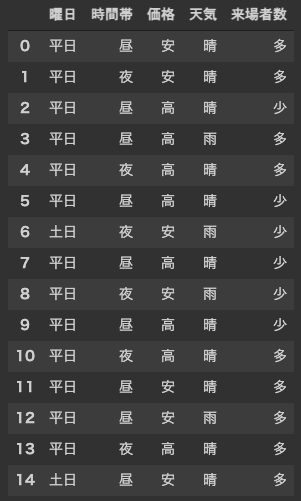
今回は,曜日(平日 or 土日) , 時間帯(昼 or 夜) ,価格(高 or 安), 天気(晴 or 雨) の情報を利用して, イベントの 来場者数(多 or 少) を分類(予測)してみましょう. 学習用のデータには15のサンプルが含まれています. また,学習用のデータの表現のため,データフレーム(Excelの表のようなもの)を利用します. これまでの行列とは異なり,データフレームには 属性名(列名) を設定することが可能です.
[In:]
df = pd.DataFrame(
{
"曜日": ["平日","平日","平日","平日","平日","平日","土日","平日","平日","平日","平日","平日","平日","平日","土日"],
"時間帯":["昼","夜","昼","昼","夜","昼","夜","昼","夜","昼","夜","昼","昼","夜","昼"],
"価格":["安","安","高","高","高","高","安","高","安","高","高","安","安","高","安"],
"天気":["晴","晴","晴","雨","晴","晴","雨","晴","雨","晴","晴","晴","雨","晴","晴",],
"来場者数":["多","多","少","多","多","少","少","少","少","少","多","多","多","多","多",]
}
)
display(df)
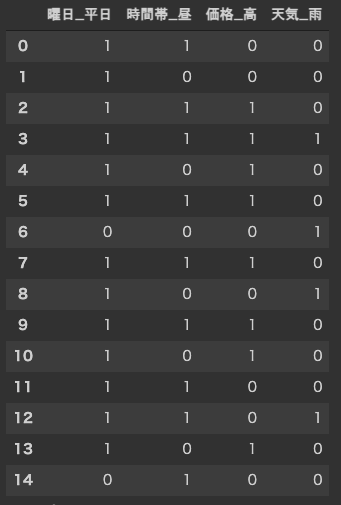
決定木の生成には,機械学習のライブラリである scikit-learn を利用しますが, “平日"や"“土日"などの 質的変数 を扱うことができないため,上記のデータフレームを ダミー変数 に変換する必要があります(R言語の rpart なら質的変数のままでも可能). ダミー変数とは,文字列などの質的変数を,量的変数(数値) で表したものです. 例えば “平日"を"1”,“土日"を"0"として表します. ダミー変数への変換は,Pandasの get_dummies 関数を用いるだけです(多重共線性を避けるため drop_first=True を設定しています).
[In:]
data = df[["曜日","時間帯","価格","天気"]]
target = df["来場者数"]
data = pd.get_dummies(data, drop_first=True) #ダミー変数の生成
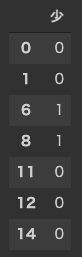
target = pd.get_dummies(target, drop_first=True)
display(data)
display(target)
決定木のアルゴリズム
それでは, 今回のテーマである 決定木 について考えていきましょう. 決定木は,これまでに紹介したロジスティック回帰やK近傍法のように分類(予測)のための手法です. 分類のプロセスが 木構造 で表されることから,その名前が付けられました. 決定木を生成するためには,ID3,C4.5,CART などのアルゴリズムが提案されています. これらのアルゴリズムは,エントロピー(平均情報量) や ジニ係数 を基準に, サンプルの分割することを繰り返すことで,木構造を形成するという特徴を持ちます. ここでは,エントロピーを利用した,サンプルの分割に関して解説します.
情報量
情報量 とは,ある事象が起こった際の,起こりにくさを表す尺度です. 事象を$E$,その事象が発生する確率を$P(E)$とすると,下記の式で情報量$I(E)$を求めることができます(対数の底は$2$とすることが多いです).
$$I(E) = \log_2\left( \frac{1}{P(E)} \right) = - \log_2( P(E) )$$
例えば,いびつな形のサイコロを考えてみましょう. このサイコロは,1の目が出やすく,他の2,3,4,5,6の目は出にくいという特殊な形状だとします(確率は表に記載). ここで,1の目が出る情報量を求めると,
$$I(1の目) = - \log_2( P(1の目) ) = - \log_2( 0.5 ) = 1$$
また,2の目が出る情報量を求めると,
$$I(2の目) = - \log_2( P(2の目) ) = - \log_2( 0.1 ) = 3.32$$
となります. このように,めったに起こることがない事象は情報量が 大きく, 頻繁に起こる事象は情報量が 小さく なるという特徴を持ちます.
| 事象$E$(サイコロの目) | 確率$P(E)$ | 情報量$I(E)$ |
|---|---|---|
| 1 | 0.5 | 1 |
| 2 | 0.1 | 3.32 |
| 3 | 0.1 | 3.32 |
| 4 | 0.1 | 3.32 |
| 5 | 0.1 | 3.32 |
| 6 | 0.1 | 3.32 |
平均情報量(エントロピー)
平均情報量(エントロピー) とは,上記の 情報量 の期待値(平均値)です. 確率変数(サイコロ)を$X$,結果として起こりうる事象(1,2,3,4,5,6の目)を$E_i$とすると,下記の式でエントロピー$H(X)$を求めることができます.
$$H(X) = \sum_{E_i} P(E_i) \cdot I(E_i)$$
例えば,上記のサイコロの例で,エントロピーを求めると,
$$H(サイコロ) = P(1の目) \cdot I(1の目) + \cdots + P(6の目) \cdot I(6の目) $$
$$H(サイコロ) = 0.5 \cdot 1 + (0.1 \cdot 3.32) \times 5 = 2.16$$
となります. エントロピーは,事象の発生確率が,均一であるほど 大きく, 偏りがあるほど 小さく なるという特徴を持ちます.
データセット(分割前)のエントロピー
それでは,来場者数のデータセットのエントロピーを計算してみましょう. 15のサンプルにおいて,来場者が多となる確率は $9 / 15$ ,少となる確率は $6 / 15$ です. この確率を基にエントロピーを計算すると$0.97$となります.
| 事象$E$(来場者数) | 確率$P(E)$ | 情報量$I(E)$ |
|---|---|---|
| 多 | 9 / 15 | 0.74 |
| 少 | 6 / 15 | 1.32 |
[In:]
#エントロピーの定義
def entropy(probs):
value = (probs * -1 * np.log2(probs)).sum()
return value
#分割前のエントロピー
probs = np.array([9/15, 6/15])
e = entropy(probs)
print(e)
[Out:]
0.9709505944546686
データセット(分割後)のエントロピー
ここでは,価格 でデータセットを分割してみましょう. 価格が 高 は8サンプル,安 は7サンプルとなります.
[In:]
high = data[data["価格_高"] == 1]
low = data[data["価格_高"] == 0]
target_high = target.loc[high.index]
display(target_high)
target_low = target.loc[low.index]
display(target_low)
分割したそれぞれのデータセットで,エントロピーを計算すると, 高のエントロピーは $1.00$,安のエントロピーは $0.86$ となりました.
(価格=高)
| 事象$E$(来場者数) | 確率$P(E)$ | 情報量$I(E)$ |
|---|---|---|
| 多 | 4 / 8 | 1 |
| 少 | 4 / 8 | 1 |
(価格=安)
| 事象$E$(来場者数) | 確率$P(E)$ | 情報量$I(E)$ |
|---|---|---|
| 多 | 5 / 7 | 0.49 |
| 少 | 2 / 7 | 1.80 |
[In:]
#分割後(価格_高)のエントロピー
probs_high = np.array([4/8, 4/8])
e_high = entropy(probs_high)
print(e_high)
#分割後(価格_低)のエントロピー
probs_low = np.array([2/7, 5/7])
e_low = entropy(probs_low)
print(e_low)
[Out:]
1.0
0.863120568566631
このエントロピーの期待値を求め,分割前のエントロピーとの差を計算すると$0.035$となります. この値は 情報利得(Information Gain) と呼ばれ,分割後のデータが偏るほど(不純度が減ると),大きな値となります. 例えば,分割後のデータセットが,全て"多”,または,全て"少"となるとき,情報利得は最大となります. 全ての属性(曜日,時間帯,価格,天気)の情報利得を調べると,下記の表のようになり, 最も値の大きい 価格 が分割のための基準として採用されます. この操作を繰り返すことで,決定木が生成されます.
| 属性 | 情報利得 |
|---|---|
| 曜日 | 0.005 |
| 時間帯 | 0.009 |
| 価格 | 0.035 |
| 天気 | 0.011 |
[In:]
#情報利得の定義
def gain(data, target, attr):
probs = np.array([target.sum() / len(target), (len(target) - target.sum()) / len(target)])
e = entropy(probs) #分割前のエントロピー
t = data[data[attr] == 1]
f = data[data[attr] == 0]
target_t = target.loc[t.index]
target_f = target.loc[f.index]
probs_t = np.array([target_t.sum() / len(target_t), (len(target_t) - target_t.sum()) / len(target_t)])
probs_f = np.array([target_f.sum() / len(target_f), (len(target_f) - target_f.sum()) / len(target_f)])
e_t = entropy(probs_t) #分割後のエントロピー
e_f = entropy(probs_f)
g = e - ((len(t) / len(data)) * e_t + (len(f) / len(data)) * e_f) #情報利得
return g
g_price = gain(data, target, "曜日_平日")
print(g_price)
g_price = gain(data, target, "時間帯_昼")
print(g_price)
g_price = gain(data, target, "価格_高")
print(g_price)
g_price = gain(data, target, "天気_雨")
print(g_price)
[Out:]
0.004545537028176172 #曜日_平日
0.008986624929939513 #時間帯_昼
0.03482766245690749 #価格_高
0.010799704414199196 #天気_雨
scikit-learnで決定木
それでは,機械学習のライブラリである scikit-learn を利用して決定木を生成してみましょう. scikit-learnでは, CART と呼ばれるアルゴリズムで決定木を生成します. また, 分割の基準として標準では ジニ係数 が用いられますが,ここでは上記で説明した エントロピー を利用します. 決定木の生成には tree.DecisionTreeClassifier 関数を用います. ここで,基準(criterion)を entropy ,木の最大の深さ(max_depth)を 3 , 乱数のシード(random_state)を 0 に固定しています.
t = tree.DecisionTreeClassifier(criterion="entropy", max_depth=3, random_state=0)
t = t.fit(data, target)
生成された決定木をplt_treeで可視化します.
figsizeはグラフの大きさを設定しています.
[In:]
plt.figure(figsize=(12, 8))
plot_tree(t, feature_names=data.columns, filled=True)
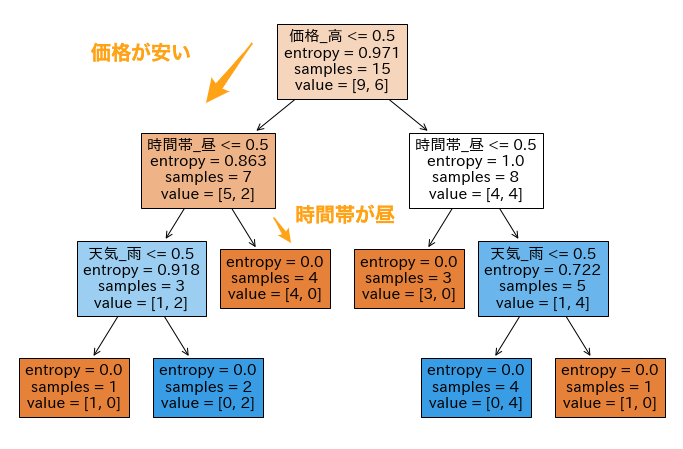
下図が生成された決定木です. 決定木の根(ルート)から,属性に基づき分類し,最終的に到達する葉(リーフ)で 多(0) か 少(1) かを判定します. 例えば,価格_高 <= 0.5 は,チケット価格(価格_高)による分類であり,True は安(0),False は高(1)を表しています. 例えば,価格が安く(価格_高 <= 0.5がTrue),お昼に開催される(時間帯_昼 > 0.5がFalse)ときは,来場者は 多 となることがわかります.
最後に,predict 関数を利用して,決定木に対数する入力と出力の関係を確認します. 例えば,「平日(1),昼(1),安(0),晴(0)」を入力すると,来場者数の予測は「多(0)」という結果が得られます.
[In:]
result = t.predict([[1, 1, 0, 0]]) #平日,昼,安,晴
print(result) #多
result = t.predict([[1, 0, 0, 0]]) #平日,夜,安,晴
print(result) #多
result = t.predict([[1, 1, 1, 0]]) #平日,昼,高,晴
print(result) #少
[Out:]
[0]
[0]
[1]
課題
タイタニックのデータセットを利用して, 生存結果(0:死亡,1:生存)を分類するための決定木を作成してください.
df = pd.DataFrame({
'生存結果': {0: 0, 1: 1, 2: 1, 3: 1, 4: 0, 5: 0, 6: 0, 7: 1, 8: 1, 9: 1, 10: 1, 11: 0, 12: 0, 13: 0, 14: 1, 15: 0, 16: 0, 17: 0, 18: 1, 19: 1},
'階級': {0: 3, 1: 1, 2: 3, 3: 1, 4: 3, 5: 1, 6: 3, 7: 3, 8: 2, 9: 3, 10: 1, 11: 3, 12: 3, 13: 3, 14: 2, 15: 3, 16: 3, 17: 2, 18: 2, 19: 3},
'性別': {0: 'male', 1: 'female', 2: 'female', 3: 'female', 4: 'male', 5: 'male', 6: 'male', 7: 'female', 8: 'female', 9: 'female', 10: 'female', 11: 'male', 12: 'male', 13: 'female', 14: 'female', 15: 'male', 16: 'female', 17: 'male', 18: 'male', 19: 'female'},
'年齢': {0: 22, 1: 38, 2: 26, 3: 35, 4: 35, 5: 54, 6: 2, 7: 27, 8: 14, 9: 4, 10: 58, 11: 20, 12: 39, 13: 14, 14: 55, 15: 2, 16: 31, 17: 35, 18: 34, 19: 15},
'乗船料金': {0: 7.25, 1: 71.2833, 2: 7.925, 3: 53.1, 4: 8.05, 5: 51.8625, 6: 21.075, 7: 11.1333, 8: 30.0708, 9: 16.7, 10: 26.55, 11: 8.05, 12: 31.275, 13: 7.8542, 14: 16.0, 15: 29.125, 16: 18.0, 17: 26.0, 18: 13.0, 19: 8.0292}
})
課題を完成させたら,chapter11.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定