分類④・k近傍法
ノートブックの作成
Colabにアクセスし,新規にノートブックを作成してください. ノートブックのタイトルは chapter10 とします. また,numpy,matplotlib.pyplot に加え,機械学習ライブラリのscikit-LearnとSciPyをインポートします.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.neighbors import KNeighborsClassifier
import scipy.stats as stats
データの準備
あらかじめ用意された機械学習のための データセット を利用することができます. ここでは,scikit-learn ライブラリに収録されている アヤメ(iris) のデータセットを用います. アヤメは草地に生息している植物であり, setosa, versicolor, virginica などの種類があります(和名はよく分かりませんでした). このデータセットには,上記3種類のアヤメの, がく片の長さ(Sepal Length) ,がく片の幅(Sepal Width) , 花弁の長さ(Petal Length) ,花弁の幅(Petal Width) を計測したデータが含まれています.
各種類に50のサンプルがあり,例えば,最初のデータは[5.1,3.5,1.4, 0.2]となっています. これは,がく片の長さが5.1cm,がく片の幅が3.5cm,花弁の長さが1.4cm,花弁の幅が0.2cmを表しています. ラベルは0,1,2のいずれかで与えられ,それぞれsetosa,virsicolor, virginicaを表しています. 最初のサンプルのラベルは0であるため,これは setosa であることがわかります.
[In:]
iris = load_iris()
print(iris.feature_names) #フィールド名
print(iris.data[0:5]) #フィールド・データ
print(iris.target_names) #ラベル名
print(iris.target[0:5]) #ラベル・データ
[Out:]
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]]
['setosa' 'versicolor' 'virginica']
[0 0 0 0 0]
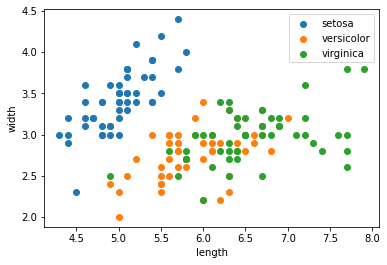
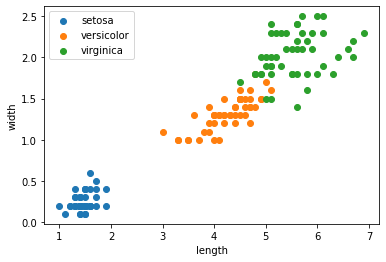
ここでは,簡単化のため,がく片の長さ と がく片の幅 のみ対象とします. 散布図をプロットしてみると,versicolorとvirginicaの分類は難しそうだということがわかります.
length = iris.data[:,0]
width = iris.data[:,1]
target = iris.target
setosa = np.where(target == 0)
versicolor = np.where(target == 1)
virginica = np.where(target == 2)
plt.scatter(length[setosa],width[setosa], label="setosa")
plt.scatter(length[versicolor],width[versicolor], label="versicolor")
plt.scatter(length[virginica],width[virginica], label="virginica")
plt.legend()
plt.xlabel("length")
plt.ylabel("width")
学習データとテストデータ
今回はデータセットに含まれる150のサンプルを 学習データ(訓練データ) と テストデータ(評価データ) に分けることにします. このように,対象のサンプルを学習用とテスト用に分けて, 回帰や分類の妥当性の検証に用いる方法を 交差検証 と呼びます. サンプルを分ける際は,偏りがないように,無作為に抽出することが必要です. ここでは,numpyの shuffle 関数を用いて,サンプルをシャッフルした後で, 前方の100のサンプルを学習データ,後方の50のサンプルをテストデータとします. シャッフルの結果は,実行する度に変化することに注意してください.
[In:]
z = list(zip(length, width, target)) #要素を一つのリストにまとめる
np.random.shuffle(z) #シャッフル
length,width,target = zip(*z) #要素を分割する
length = np.array(length)
width = np.array(width)
target = np.array(target)
print(length[0:5])
print(width[0:5])
print(target[0:5])
[Out:]
[6.2 6.3 5.2 5.4 5.8]
[2.2 2.5 3.5 3. 2.7]
[1 1 0 1 1]
l_length = length[0:100] #学習データ
l_width = width[0:100]
l_target = target[0:100]
t_length = length[100:150] #テストデータ
t_width = width[100:150]
t_target = target[100:150]
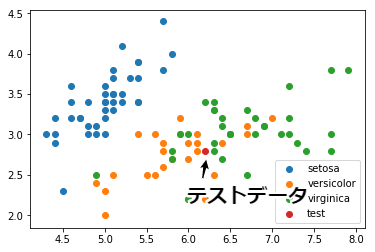
それでは,100の学習データと,1つのテストデータを散布図にプロットしてみます. 図中の赤いサンプルがテストデータです. このテストデータが,どのカテゴリ(setosa,versicolor,virginica)に分類されるかを考えます.
setosa = np.where(l_target == 0)
versicolor = np.where(l_target == 1)
virginica = np.where(l_target == 2)
plt.scatter(l_length[setosa], l_width[setosa], label="setosa")
plt.scatter(l_length[versicolor], l_width[versicolor], label="versicolor")
plt.scatter(l_length[virginica], l_width[virginica], label="virginica")
plt.scatter(t_length[0], t_width[0], label="test") #テスト用のデータ
plt.legend()
k近傍法
今回取り上げる手法は k近傍法(k-Nearest Neighbor: k-NN) です. これまでに解説した,線形判別分析(LDA) や ロジスティック回帰 に比べると, とっても単純な仕組みで動作しますが,サンプル数が十分にあれば,高い精度を得られるとされています. また,ロジスティック回帰など,$w_1 \cdot x + w_0$といった特定の関数(分布)に従うことを前提に, 最適なパラメータを導出する手法は パラメトリック な手法と呼ばれるのに対し, k近傍法は,特定の関数(分布)の前提を持たないことから ノンパラメトリック な手法と呼ばれます. 加えて,パラメータの導出など事前の計算が不要なことから 怠惰学習 とも呼ばれます(なんだか不名誉な印象ですね).
それでは,k近傍法の仕組みを見ていきましょう. まずは,分類対象であるテスト用のサンプルから,距離的に近いサンプルを$k$個抽出します. 距離は様々に定義することが出来ますが,ここでは ユークリッド距離 を採用します. ユークリッド距離はnumpyの norm 関数で求めることができます. map 関数を利用して「テスト用のサンプル」と「他の全てのサンプル」の間の距離を計算しています.
[In:]
v = np.c_[l_length - t_length[0], l_width - t_width[0]] #ベクトルで表現
d = np.array(list(map(lambda x: np.linalg.norm(x), v))) #ユークリッド距離の計算
print(v[0:5])
print(d[0:5])
[Out:]
[[ 0.1 0. ]
[-0.1 0. ]
[ 0.1 0.1]
[-0.1 0.1]
[-0.2 -0.1]]
[0.1 0.1 0.14142136 0.14142136 0.2236068 ]
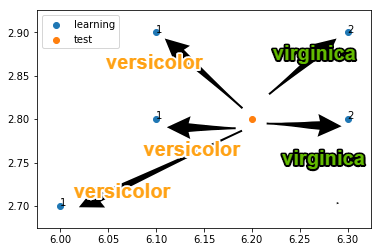
次に,求めた距離を基準として,学習データを昇順でソートします. この結果,ソートされたリストの [0:k] が,距離が近い$k$個のサンプルとなります. ここでは,$K=5$とした結果,そのラベルは$2,1,2,1,1$となったことが分かります($1$はversicolor,$2$はvirginica).
[In:]
z = list(zip(d, l_length, l_width, l_target)) #要素を一つのリストにまとめる
z.sort() #昇順でソート
d,l_length,l_width,l_target = zip(*z) #要素を分割する
d = np.array(d)
l_length = np.array(l_length)
l_width = np.array(l_width)
l_target = np.array(l_target)
k = 5
print(d[0:k])
print(l_target[0:k])
[Out:]
[0.1 0.1 0.14142136 0.14142136 0.2236068 ]
[2 1 2 1 1]
この$k=5$個のサンプルで,ラベルの多数決(最頻値)を行います. このケースでは,多数決の結果, 1(Versicolor) が最も多く,3個の出現頻度であったことがわかります. よって,このテスト用のサンプルを 1(Versicolor) に分類します. このようにk近傍法では,事前に学習は不要であり,多数決という単純な仕組みで結果を得ます.
[In:]
value,number = stats.mode(l_target[0:k]) #最頻値
print(value)
print(number)
[Out:]
[1] #最頻値(Versicolor)
[3] #出現回数
k = 5
plt.scatter(l_length[0:k], l_width[0:k], label="learning")
plt.scatter(t_length[0], t_width[0], label="test")
plt.legend()
for i in range(k):
plt.annotate(l_target[i], (l_length[i], l_width[i]))
分類精度
最後に分類精度を確認しておきましょう. 分類精度を評価するための基準も様々に存在しますが, 今回は 正解率(Accuracy) のみに注目します(この他にも 適合率(Precision) ,再現率(Recall) などがあります). 正解率は,テストデータのうち,予測結果が正解であった割合です. ここでは,50個のテストデータのうち,35個が正解,15個が不正解であったため, 正解率は$35/(35 + 15) = 0.7$となります(この値は交差検証のデータに依存します).
[In:]
positive = 0
negative = 0
for t in zip(t_length, t_width, t_target):
v = np.c_[l_length- t[0], l_width - t[1]]
d = np.array(list(map(lambda x: np.linalg.norm(x), v)))
z = list(zip(d, l_length, l_width, l_target))
z.sort()
d,l_length,l_width,l_target = zip(*z)
d = np.array(d)
l_length = np.array(l_length)
l_width = np.array(l_width)
l_target = np.array(l_target)
k = 5
value,number = stats.mode(l_target[0:k]) #最頻値
if value == t[2]:
positive += 1
else:
negative += 1
print(positive) #正解数
print(negative) #不正解数
print(positive / (positive + negative)) #正解率
[Out:]
35
15
0.7
scikit-learnでk近傍法
最後にscikit-Learnで提供されている k近傍法のライブラリ KNeighborsClassifer を利用して分類してみましょう.
[In:]
# 学習データ
X = np.array(list(zip(l_length, l_width)))
Y = np.array(l_target)
# K=5で学習
k = 5
nn = KNeighborsClassifier(n_neighbors=k)
nn.fit(X, Y)
# 評価データ
T = np.array(list(zip(t_length, t_width)))
# k近傍法で分類を予測
values = nn.predict(T)
print(values)
# 正解率
acc = np.sum(values == t_target) / len(values)
print(acc)
[Out:]
[1 0 2 1 0 0 1 2 2 2 1 0 1 2 1 1 1 1 1 1 0 2 2 2 1 0 0 0 2 2 0 2 1 2 1 2 1
0 1 2 0 0 0 1 1 1 1 0 1 2]
0.74
課題
アヤメ(iris)のデータセットにおいて,花弁の長さ(Petal Length)と花弁の幅(Petal Width)を利用して,k近傍法で分類せよ. データセットをシャッフルした後で,学習用の100サンプルとテスト用の50サンプルに分け,交差検証で正解率を求めよ. このとき,k近傍法のライブラリ KNeighborsClassifier を利用して構わない.
length = iris.data[:,2] # 花弁の長さ
width = iris.data[:,3] # 花弁の幅
target = iris.target
setosa = np.where(target == 0)
versicolor = np.where(target == 1)
virginica = np.where(target == 2)
plt.scatter(length[setosa],width[setosa], label="setosa")
plt.scatter(length[versicolor],width[versicolor], label="versicolor")
plt.scatter(length[virginica],width[virginica], label="virginica")
plt.legend()
plt.xlabel("length")
plt.ylabel("width")
課題を完成させたら,chapter10.ipynb を保存し, 共有用のリンク と ノートブック(.ipynb) をダウンロードして提出してください. このとき,必ず事前に下記の設定を行ってから提出してください.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定
- 共有設定で「学校法人椙山女学園大学」を「閲覧者」に設定