インデックス
インデックスとは
データベースの検索効率を向上させるために用いられるのが インデックス(索引) です. 一般にSQLiteなどのリレーショナル・データベースでは,インデックスは自動的に作成されますが, ユーザが意図してインデックスを作成するためのSQL文も用意されています. インデックスを作成する際の注意点を挙げます.
- データ量の多いデータベースにインデックスを作成する(データが少ない場合はパフォーマンスが低下)
- カーディナリティ(属性に含まれる値のバリエーション)が高い属性でインデックスを作成する
- WHERE区の条件などに用いられる属性でインデックスを作成する.
ここでは,次の16のレコードを含むテーブルを例とします. ID と NAME の属性で構成され,主キーは ID です. このテーブルから Alex を検索するときのパフォーマンスを考えます.
| ID | NAME |
|---|---|
| 23 | Chris |
| 20 | David |
| 9 | Greg |
| 22 | Allen |
| 11 | Carl |
| 29 | Rajiv |
| 6 | Jordan |
| 4 | Alex |
| 26 | Ashly |
| 19 | Nancy |
| 2 | Emily |
| 27 | Norma |
| 18 | Christine |
| 28 | Joy |
| 12 | Maria |
| 3 | Alice |
インデックスはデータ構造に依存して,パフォーマンスが決まります. データベースでは,B木(B-tree) が用いられますが, ここでは比較のため 線形探索 と 2分探索木 を取り上げます.
- 線形探索(Linear Search)
- 2分探索木(Binary Search Tree)
- B木(B-tree)
線形探索
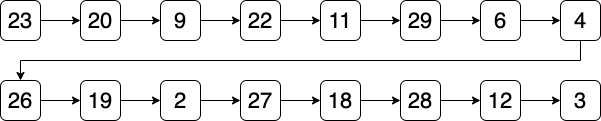
データベースでインデックスが作成されていない状態では,線形探索 となります. 検索キーとなる ID はリスト形式で管理され,リストの先頭から順に比較されます. 例えば,ID=4(Alex) を検索するときは, リストの先頭から23,20 ,9,…という順番で比較し, 8番目の比較で ID=4 を発見できます. 探索回数は最少で1回(ID=23のとき),最多で16回(ID=3のとき)となります. 要素数が$n$のとき,時間計算量を表すO記法では$O(n)$と表されます.
2分探索木
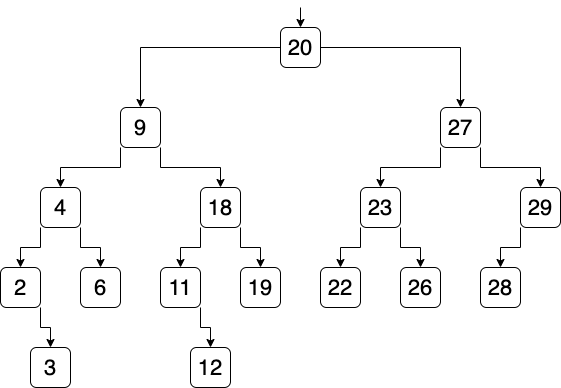
線形探索では効率が悪いため木構造のインデックスが採用されます. まずは基本となる 2分探索木 を紹介します. 2分探索木では,ノードが ID を表しており, 「左の子は親より値が小さく」,「右の子は親より値が大きい」という特徴があります. 木の根(ルート)から探索をスタートし,値の大小を比較しながら,リンクを辿って検索します. 例えば,ID=4(Alex) を検索するときは,木の根の20と比較します. $4 < 20$ であるため,左の子へのリンクを辿って9と比較します. $4 < 9$であるため,左の子へのリンクを辿って4を発見します.
探索回数は最少で1回(ID=20のとき),最多で5回(ID=3またはID=12のとき)となります. 一般に,木の高さは$\lfloor log_2(n) \rfloor= \lfloor log_2(16) \rfloor =4$以上であり(床関数$\lfloor x \rfloor$は「切り捨て」を表す), 最多の探索回数は5回以上となることが知られています(木の高さは0から数えるため,高さが4のとき探索回数は5回となる). また,平衡を維持する2分探索木は AVL木 と呼ばれ,純粋な2分探索木よりも探索効率が向上します. 要素数が$n$のとき,平衡状態の時間計算量を表すO記法は$O(log(n))$と表されます.
| 木の高さ($log_2(n)$) | 下層(葉)のデータ数 | 最大データ数($n$) | 探索回数 |
|---|---|---|---|
| 0 | 1 | 1 | 1 |
| 1 | 2 | 3 | 2 |
| 2 | 4 | 7 | 3 |
| 3 | 8 | 15 | 4 |
| 4 | 16 | 31 | 5 |
| 5 | 32 | 63 | 6 |
| 6 | 64 | 127 | 7 |
| 7 | 128 | 255 | 8 |
| 8 | 256 | 511 | 9 |
| 9 | 512 | 1023 | 10 |
| 10 | 1024 | 2047 | 11 |
B木
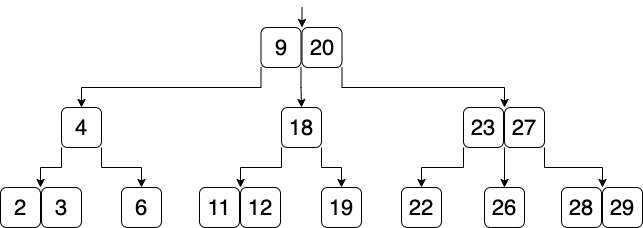
実際のリレーショナル・データベースでは,B木 によるインデックス作成されます(または B+木). B木は,2分探索木の分岐数を最大$m$に一般化したものです. ノードには複数の ID が記録され,値に応じて複数の分岐が存在します. 例えば,ID=4(Alex) を検索するときは,木の根の9と20を比較します. このとき,9より小さければ左の子,9より大きく20より小さいときは中央の子,20より大きいときは右の子を辿ります. $4<9$であるため,左の子へのリンクを辿って,4を発見します. $m$が大きい場合,各ノードで線形探索と同じ計算量が発生するため,2分探索木より効率が悪いように見えます. しかし,ハードディスクなどの外部記憶装置の場合は,ブロック単位でデータを参照する方が効率が良いためB木が採用されます.
SQLでインデックス
google colaboratoryを利用して, リレーショナル・データベース(SQLite)におけるインデックスの効果を検証してみましょう. SQLでインデックスを作成するには,CREATE INDEX文 を用います.
CREATE INDEX インデックス名 ON テーブル名(属名)
また,SQLでインデックスを削除するには,DROP INDEX文 を用います.
DROP INDEX インデックス名
ここでは,PythonのSQLiteのライブラリを導入します.
import sqlite3
import random
1〜200,000までの整数を生成し,ランダムに100,000個の整数を選択します. この100,000個の整数をリレーショナル・データベースに登録することにします.
key_size = 200000 #@param {type: "number"}
sample_size = 100000 #@param {type: "number"}
list = random.sample(range(key_size), sample_size)
リレーショナル・データベースを構築します.
# SQLite
con = sqlite3.connect('sample.db')
cur = con.cursor()
CREATE TABLE文 でIDだけで構成されるテーブルを生成します. ランダムに選ばれた100,000個の整数をレコードとして登録します.
cur.execute("CREATE TABLE IF NOT EXISTS sample(ID integer)")
for key in list:
cur.execute(f"INSERT INTO sample VALUES({key})")
100,000個の整数から,1つの整数を選び, SELECT文 で検索します. 同じ値の整数が検索結果となっていることがわかります.
# 探索対象
target = random.sample(list, 1)[0]
print(f"target={target}")
# SELECT文
result = cur.execute(f"SELECT * FROM sample where ID={target}")
print(f"result={result.fetchone()[0]}")
target=188372
result=188372
上記と同じ検索を1,000回繰り返し,応答時間を計測します. 応答時間は 2.9秒 となりました.
%%time
# SELECT文を1000回繰り返す
for step in range(1000):
target = random.sample(list, 1)[0]
result = cur.execute(f"SELECT * FROM sample where ID={target}")
CPU times: user 2.8 s, sys: 91.6 ms, total: 2.89 s
Wall time: 2.9 s
次にIDでインデックスを作成し,同じように1,000回の検索を行います. 応答時間は 30.5ミリ秒(0.03秒) となりました. インデックスがあると約100倍の高速化が確認できます.
# インデックスの作成
cur.execute("CREATE INDEX myindex ON sample(id)")
%%time
# SELECT文を1000回繰り返す
for step in range(1000):
target = random.sample(list, 1)[0]
result = cur.execute(f"SELECT * FROM sample where ID={target}")
CPU times: user 23.9 ms, sys: 947 µs, total: 24.8 ms
Wall time: 30.5 ms
確認のため,インデックスを削除し,再度,1000回の検索を行います. 応答時間は 2.85秒 となりました. インデックスによる高速化が確認できました.
# インデックスの削除
cur.execute("DROP INDEX myindex")
%%time
# SELECT文を1000回繰り返す
for step in range(1000):
target = random.sample(list, 1)[0]
result = cur.execute(f"SELECT * FROM sample where ID={target}")
CPU times: user 2.75 s, sys: 94.3 ms, total: 2.84 s
Wall time: 2.85 s
2分探索木とB木の可視化
サンフランシスコ大学が2分探索木とB木の可視化ツールを公開しています.