局所探索アルゴリズム・シミュレーテッドアニーリング

ノートブックの作成

Google Colaboratory を起動し，新規にノートブックを作成してください． ノートブックのタイトルは AI-9 とします． ノートブックの作成方法に関しては第1回の資料を参考にしてください．

最初に Simple AI をインストールします． セルで下記のコマンドを実行してください．

!pip install simpleai

最適化問題

今回も 最適化問題 を取り上げます．

最適化問題の状態空間モデルを確認しておきます．

シミュレーテッド・アニーリング（Simulated Annealing）

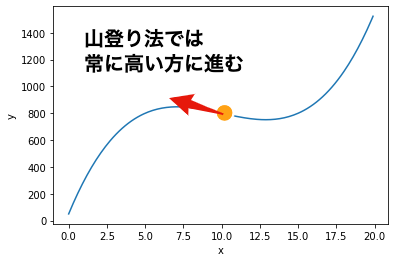
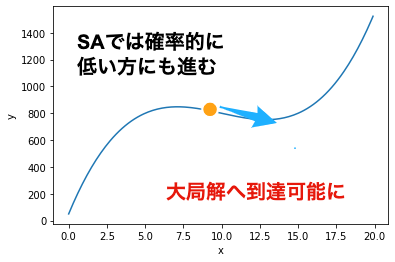
シミュレーテッド・アニーリングは日本語では焼きなまし法と呼ばれる手法で， 金属加工において，金属を熱した後で徐々に冷やしながら，金属の形状を安定させる方法に由来しています． 山登り法は評価の高い方向に必ず進むのに対し，シミュレーテッド・アニーリングでは， 遷移確率$p$に応じて評価が低い場合も受け入れることが特徴です． これにより，局所解に陥ることなく，大局解を発見できる可能性が高くなります． 一般に，遷移確率$p$は，ステップ数（時間）が経過するとともに小さな値となり， 最終的には山登り法と同様に評価が高い方向に探索を進めます．

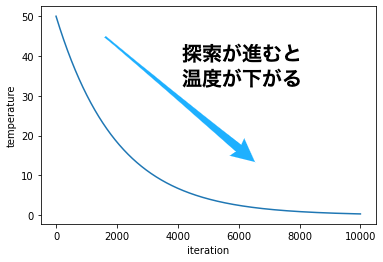
遷移確率$p$を定義するため，まずは温度パラメータ$t$を次のように定義します． ここで，$k$は温度の最大値，$\lambda$は温度の変化を決めるパラメータであり，$i$は探索数（ステップ数）を表しています． 例えば，$k=50$，$\lambda=0.0005$としたとき，下図のように温度パラメータは変化します． 最初は$t=50$から始まり，探索数（ステップ数）が経過すると，$t=0$に漸近します．

$$ t = k \cdot e^{- \lambda \cdot i} $$

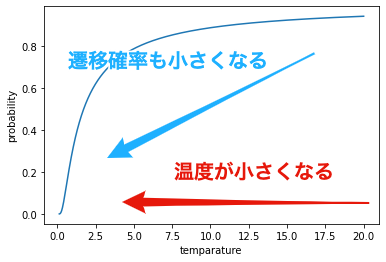
上述の温度パラメータ$t$を用いて，遷移確率$p$を次のように定義します． ここで，$\Delta f=f(x') - f(x)$であり，遷移後と遷移前の 評価の差 を表しています． $\Delta f \geq 0$のときは，評価が改善されるため遷移確率$p=1$となります． 一方で，$\Delta f < 0$のときは，評価が改悪されるため遷移確率$p<1$となります． このとき，温度パラメータ$t$が小さくなると，遷移確率$p$も小さくなるように設計されています．

$$ p = 1　(\Delta f \geq 0) $$

$$ p = e^{ \frac{\Delta f}{t}}　(\Delta f< 0) $$

実装

最初にライブラリをインポートします． 探索問題の型 を表すSearchPrblemに加え， 山登り法 を表す hill_climbingと シミュレーテッド・アニーリングを表すsimulated_annealingをインポートします． また，数値計算やグラフ描画のために，Numpy，Matplotib，random, mathもインポートします．

import numpy as np
import matplotlib.pyplot as plt
import random
import math

from simpleai.search import SearchProblem, hill_climbing, simulated_annealing

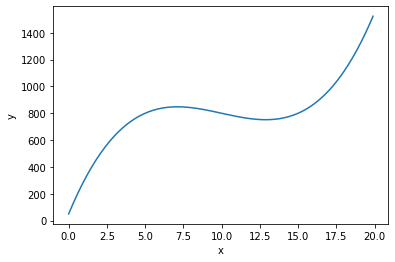
最初に関数$f(x)$を定義します． ここでは，$f(x) = f(x) = x^3 - 30 x^2 + 275x + 50$とします．

def fx(x):
    y = x**3 - 30 * x**2 + 275 * x + 50
    return y

関数をグラフに描画してみましょう． グラフの描画にはMatplotlibを用います．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("y")

次に 初期状態 を定義します． 初期状態は$x=0$に固定します．

START = 0

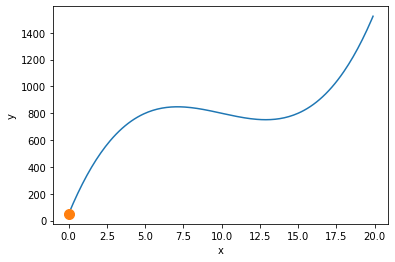
関数と初期状態を合わせてグラフを描画しましょう．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.plot(START,  fx(START),  marker="o", markersize=10)
plt.xlabel("x")
plt.ylabel("y")

インポートしたSearchProblemクラスをオーバライドして， 最適化問題を表すHillProblemを定義します． actions，result，valueは前回の山登り法のときと同じです．

class HillProblem(SearchProblem):

    def actions(self, state):

        list = []

        list.append(min(state + 0.5, 20))
        list.append(max(state - 0.5, 0))

        print("{:.3f} -> [{:.3f} {:.3f}]".format(state, list[0], list[1]))

        return list

    def result(self, state, action):
        return action

    def value(self, state):
        v = fx(state)
        return v

山登り法

まずは山登り法hill_climbingを用いて探索します．

problem = HillProblem(initial_state=START)
result = hill_climbing(problem)

最終状態と評価を確認します． 最終状態は$x=7.0$，また，その評価は$f(7.0)=848.0$であることがわかります．

print("{:.3f}".format(result.state))
print("{:.3f}".format(result.value))

7.000
848.000

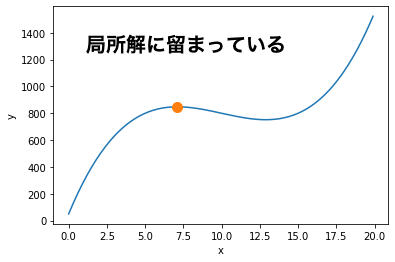
最終状態も合わせてグラフに描画します． 局所解で探索が終了していることがわかります．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.plot(result.state,  result.value,  marker="o", markersize=10)
plt.xlabel("x")
plt.ylabel("y")

シミュレーテッド・アニーリング

次に，シミュレーテッド・アニーリングを用いて探索します． まずは，温度パラメータを表すschedule関数を定義します． $k=50$，$\lambda=0.0005$に設定しています．

def schedule(iteration, k=50, l=0.0005):

    # 温度パラメータ
    t = k * np.exp(-1 * l * iteration)

    return t

温度パラメータ$t$をグラフに描画してみます． ステップ数（時間）が増加するごとに，温度パラメータが$0$に近づくことがわかります．

i  = np.arange(0, 10000, 1)
t = list(map(lambda x: schedule(x), i))

plt.plot(i, t)
plt.xlabel("iteration")
plt.ylabel("temperature")

次に遷移確率を表すprobability関数を定義します． この処理はSimpleAIに組み込まれているため定義しなくとも実行可能です． 評価の差である$\Delta$と温度パラメータ$t$に応じて遷移確率は定まります．

# 遷移確率
def probability(delta, t):
  if delta > 0:
    p = t / t # 評価が高い場合は p=1.0
  else:
    p = np.exp(delta / t)  # 評価が低い場合 p<1.0

  return p

例として，$x=8$から$x'=7$への遷移を考えます． この場合，$\Delta = f(8) - f(7) = 848 - 842 = 6 \geq 0$であり，評価が改善するため， 温度パラメータ$t$とは無関係に遷移確率$p=1$になります． つまり，必ず$x'=7$に遷移します．

# 評価が高くなる場合
y1 = fx(8) # -> 842
y2 = fx(7) # -> 848
delta = y2 - y1 # -> 6
print(f"y1={y1} y2={y2} delta={delta}")

i = np.arange(0, 10000, 1)
t = schedule(i)
p = probability(delta, t)

plt.plot(t, p)
plt.xlabel("temparature")
plt.ylabel("probability")

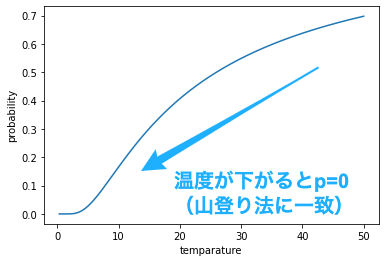
次に，$x=8$から$x'=9$への遷移を考えます． この場合，$\Delta = f(9) - f(8) = 824 - 842 = -18 < 0$であり，評価が改悪するため， 温度パラメータ$t$に応じて遷移確率$p$は定まります． 温度が高い状態では，確率$p$は高い値となりますが， 時間が経過して，温度が低くなった状態では，確率$p$は0に近づきます． つまり，探索の序盤は評価の低い状態に遷移することがありますが， 終盤になると評価の高い状態にのみ遷移するようになります．

# 評価が低くなる場合
y1 = fx(8) # 842
y2 = fx(9) # 824
delta = y2 - y1 # -> -18
print(f"y1={y1} y2={y2} delta={delta}")

i = np.arange(0, 10000, 1)
t = schedule(i)
p = probability(delta, t)

plt.plot(t, p)
plt.xlabel("temparature")
plt.ylabel("probability")

それでは，シミュレーテッド・アニーリングを適用します． 最大ステップ数（繰り返し回数）は$10000$に設定しています．

problem = HillProblem(initial_state=START)
result = simulated_annealing(problem, schedule=schedule, iterations_limit=10000)

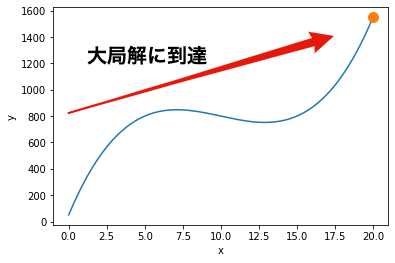
最終状態と評価を確認します． 最終状態は$x=20.0$，また，その評価は$f(20.0)=1550.0$であることがわかります． 実行するごとに異なる結果になる可能性があることに注意してください．

print("{:.3f}".format(result.state))
print("{:.3f}".format(result.value))

20.000
1550.000

最終状態も合わせてグラフに描画します． 局所解に陥ることなく，大局解に到達できたことがわかります．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.plot(result.state,  result.value,  marker="o", markersize=10)
plt.xlabel("x")
plt.ylabel("y")

課題

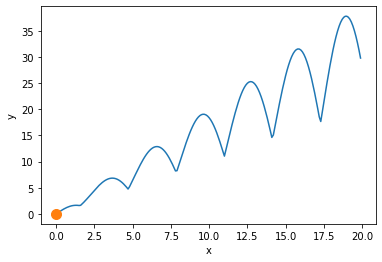
下記の関数に対してシミュレーテッドアニーリングを適用した結果を示せ． ただし，$x$の範囲は$0 \leq x \leq 20$とし，初期値は$x=0$とする．

$$ f(x) = | \cos(x) \cdot x| + x $$

Google Colaboratoryで作成した AI-9.ipynb を保存し， ノートブック（.ipynb） をダウンロードして提出しなさい． 提出の前に必ず下記の設定を行うこと．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定