局所探索アルゴリズム・山登り法

ノートブックの作成

Google Colaboratory を起動し，新規にノートブックを作成してください． ノートブックのタイトルは AI-8 とします． ノートブックの作成方法に関しては第1回の資料を参考にしてください．

最初に Simple AI をインストールします． セルで下記のコマンドを実行してください．

!pip install simpleai

最適化問題

今回は 最適化問題 を取り上げます． 最適化問題は，対象となる関数について， その値が最大（もしくは最小）となる状態を見つけることが目的となります．

最適化問題の状態空間モデルを定義します．

山登り法（Hill Climbing Method）

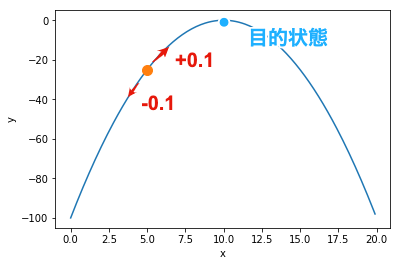
現在の状態の近傍の中で最も評価の高い状態を選択することを， 評価の改善がなくなるまで繰り返す手法です． 局所探索アルゴリズムの一つであり，最もシンプルでポピュラーな手法です．

例えば，初期状態として$x=5.0$が選ばれたとします． この$x$の近傍である$x=4.9$と$x=5.1$において，評価が改善されるかを調べます． $f(5.0)=-25.0$に対し，$f(4.9) \simeq -26.0$，$f(5.1) \simeq -24.0$であり， $x=5.1$のときに評価が改善されることが分かります． この操作を評価の改善がなくなるまで繰り返します． 最終的に$x=10$，$f(10)=0$を見つけることができれば成功です．

実装

最初にライブラリをインポートします． 探索問題の型 を表すSearchPrblemと， 山登り法 を表す hill_climbingをインポートします． また，数値計算やグラフ描画のために，Numpy，Matplotib，randomもインポートします．

import numpy as np
import matplotlib.pyplot as plt
import random

from simpleai.search import SearchProblem, hill_climbing

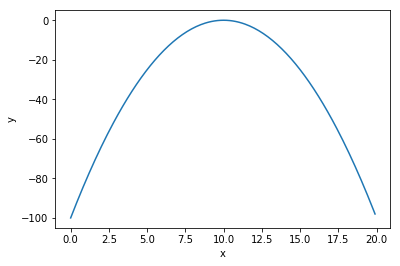
最初に関数$f(x)$を定義します． ここでは，$f(x)=-(x -10)^2$とします．

def fx(x):
    y = -(x-10)**2
    return y

関数をグラフに描画してみましょう． グラフの描画にはMatplotlibを用います． ここでは，np.arange(0, 20, 0.1)を利用して，$0.1$間隔で$0$から$20$までの等差数列を作成しています．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("y")

次に 初期状態 を定義します． 初期状態は，random.randint(0,20)を利用して，$0$から$20$の範囲の整数からランダムに選択します．

START = float(random.randint(0, 20))

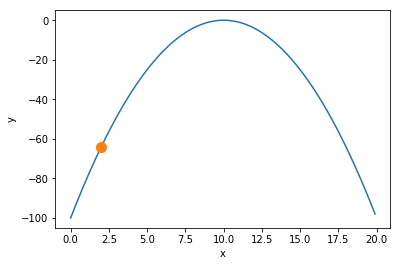
初期状態も合わせてグラフに描画します．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.plot(START,  fx(START),  marker="o", markersize=10)
plt.xlabel("x")
plt.ylabel("y")

インポートしたSearchProblemクラスをオーバライドして， 最適化問題を表すHillProblemを定義します． オーバライドするメソッドは，actions，result，valueの3種類です．

class HillProblem(SearchProblem):

    def actions(self, state):
        ...

    def result(self, state, action):
        ...

    def value(self, state):
        ...

actions(self, state)

実行可能な行動のリストを返します． 行動は$+0.1$と$-0.1$の2パターンです．

def actions(self, state):

    list = []

    list.append(min(state + 0.1, 20))
    list.append(max(state - 0.1, 0))        

    print("{:.3f} -> [{:.3f} {:.3f}]".format(state, list[0], list[1]))

    return list

result(self, state, action)

行動actionを，そのまま次の状態として扱います．

def result(self, state, action):
    return action

value(self, state)

def value(self, state):
    v = fx(state)
    return v

解の探索

山登り法hill_climbingを用いて探索します． 初期状態が$x=2$だったため，$x$を増加させる方向に探索が進んでいることがわかります．

problem = HillProblem(initial_state=START)
result = hill_climbing(problem)

2.000 -> [2.100 1.900]
2.100 -> [2.200 2.000]
2.200 -> [2.300 2.100]
2.300 -> [2.400 2.200]
(省略)
9.700 -> [9.800 9.600]
9.800 -> [9.900 9.700]
9.900 -> [10.000 9.800]
10.000 -> [10.100 9.900]

最終状態と評価を確認してみましょう． 最終状態は$x=10$，また，その評価は$f(10)=0$であることがわかります．

print("{:.3f}".format(result.state))
print("{:.3f}".format(result.value))

10.000
-0.000

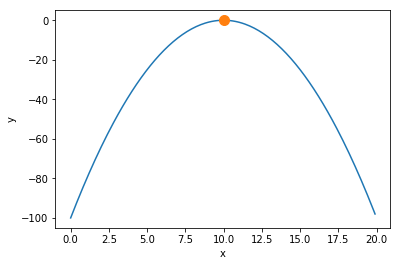
最終状態も合わせてグラフに描画します． 関数のピークを発見できていることがわかります．

x = np.arange(0, 20, 0.1)
y = fx(x)
plt.plot(x, y)
plt.plot(result.state,  result.value,  marker="o", markersize=10)
plt.xlabel("x")
plt.ylabel("y")

課題

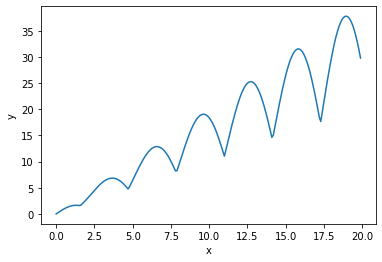
下記の関数を実装し，山登り法を適用した結果を示し，その結果を考察しなさい． ただし，$x$の範囲は$0 \leq x \leq 20$とし，初期値はランダムに選択する． ここで，xの絶対値はnp.abs(x)，余弦（cos）はnp.cos(x)で算出することができる．

$$ f(x) = | \cos(x) \cdot x| + x $$

Google Colaboratoryで作成した AI-8.ipynb を保存し， ノートブック（.ipynb） をダウンロードして提出しなさい． 提出の前に必ず下記の設定を行うこと．

• ノートブックの設定で「セルの出力を除外する」のチェックを外す
• ノートブックの変更内容を保存して固定