探索アルゴリズム・ヒューリスティック探索
ノートブックの作成
Google Colaboratory を起動し,新規にノートブックを作成してください. ノートブックのタイトルは AI-7 とします. ノートブックの作成方法に関しては第1回の資料を参考にしてください.
最初に Simple AI をインストールします. セルで下記のコマンドを実行してください.
!pip install simpleai
迷路問題
今回も前回と同じ 迷路問題を取り上げます.
迷路問題の状態空間モデルを確認しておきましょう.
状態空間モデル
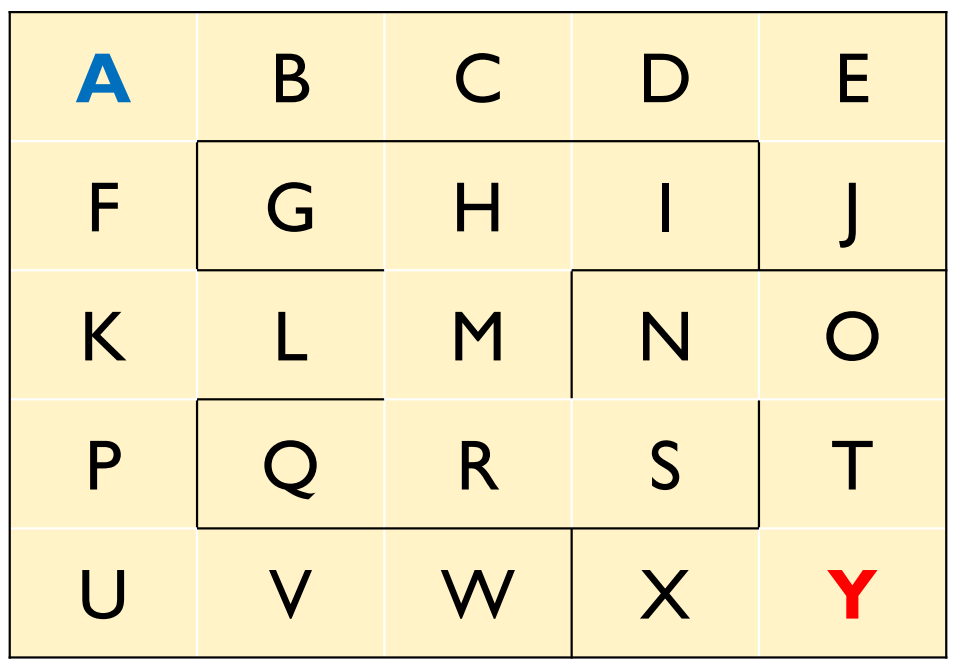
$A$から$Y$までの25の状態から,冗長な状態を取り除く.
例えば,$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E$という経路においては,$B$,$C$,$D$に分岐は存在せず,通り抜けることしかしないため,これらの状態を省略する.
この結果,$S1$から$S17$までの,17通りの状態で問題を表現する.
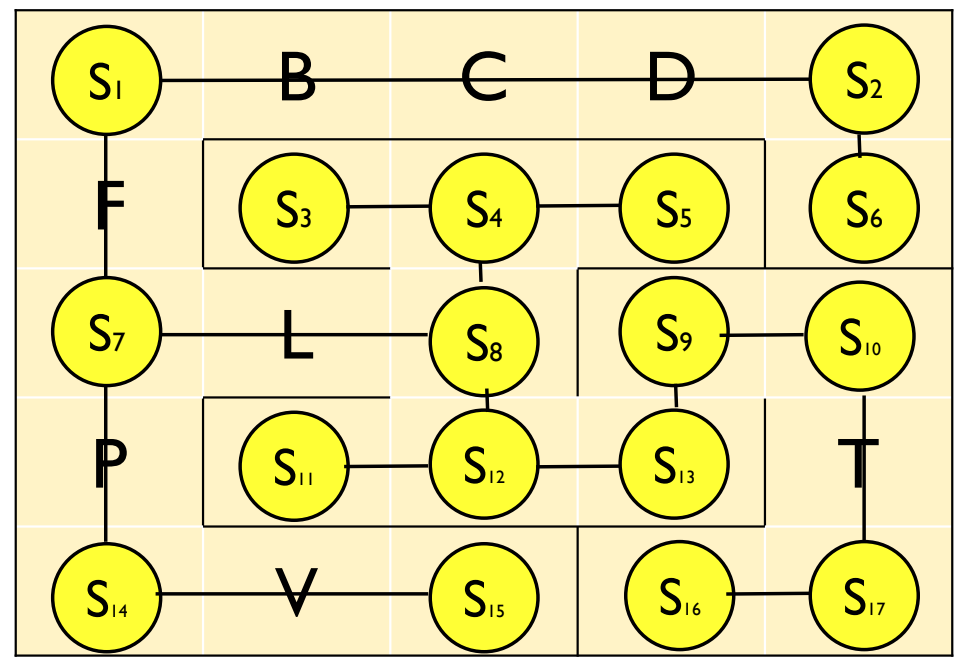 行動は移動可能な状態のペアとして定義する.
例えば,$S1$からは,$S2$と$S7$に移動可能なため,
下記のように表現できる.
行動は移動可能な状態のペアとして定義する.
例えば,$S1$からは,$S2$と$S7$に移動可能なため,
下記のように表現できる.
- $S1 \rightarrow S2$
- $S1 \rightarrow S7$
See the Pen 迷路問題 by Naoto Mukai (@nmukai) on CodePen.
ヒューリスティック探索
前回紹介した幅優先探索と深さ優先探索は知識を用いない探索手法でした. ヒューリスティック探索とは,必ずしも最適とは限られないけれど, 最適であることを推測可能な発見的(経験的な)な知識(ヒューリスティックス)を利用した探索手法のことです.
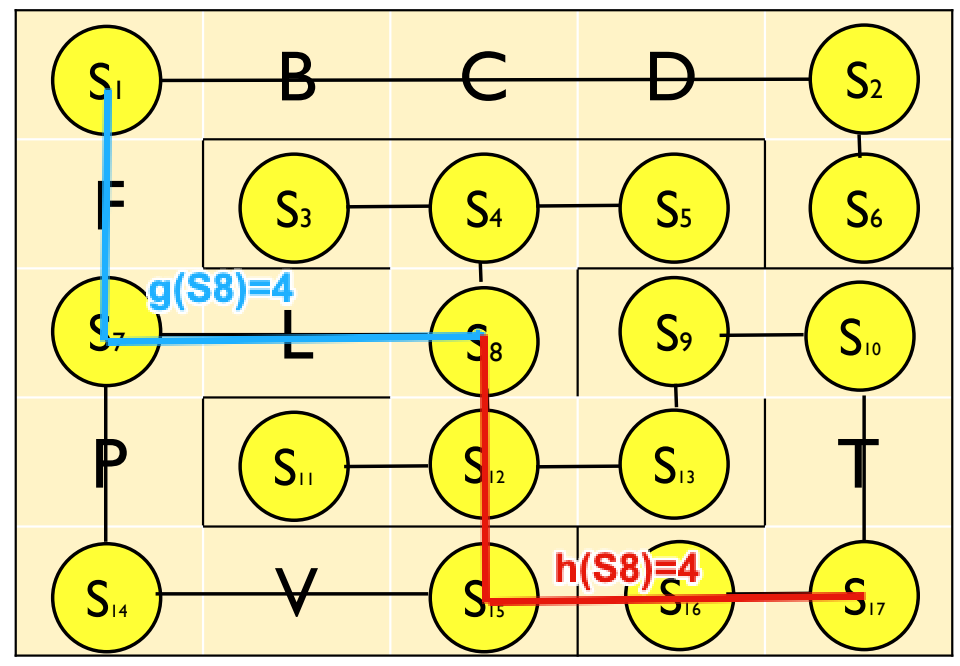
迷路問題におけるヒューリスティックスとしてマンハッタン距離を用います. マンハッタン距離とは,ある状態$S$から目的状態までの各座標(ここでは$x$座標と$y$座標)の 差の総和を距離とする指標であり, ここでは$h(S)$で表します. 例えば,$S1$から$S17$までのマンハッタン距離は, $x$座標の差は$4$,$y$座標の差は$4$であるため, これを合計して$8$になります. $$ h(S1) = 8 $$ 同様に,$S12$から$S17$までのマンハッタン距離は, $x$座標の差は$2$,$y$座標の差は$1$であるため, これを合計して$3$になります. $$ h(S12) = 3 $$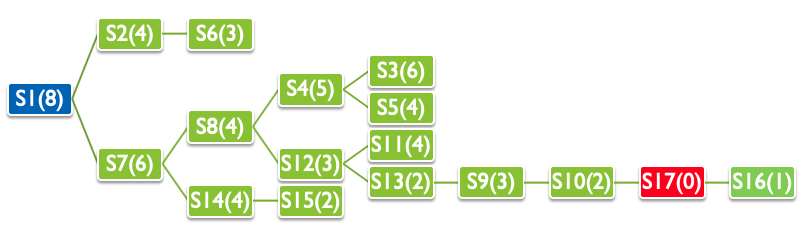
A*アルゴリズム
今回は,ヒューリスティック探索の一つである A*アルゴリズム(エースターアルゴリズム) を紹介します. A*アルゴリズムでは,下記の評価関数$f(S)$が最小となる状態を優先して探索します. $h(S)$は先に述べたマンハッタン距離を表し, $g(S)$は状態$S$に到達するまでにかかったコストを表しています. ここで注意すべきことは, $g(S)$は既に確定したコストであるのに対し, $h(S)$は将来のコストの推定値であるということです.
$$ f(S) = g(S) + h(S) $$
例えば,探索過程で$S8$に到達した場合を考えます. 初期状態の$S1$から$S8$に到達するには,$S1 \rightarrow S7 \rightarrow S8$ を辿る必要があり, そのコストは$g(S8)=4$です. 一方,$S8$から$S17$の将来のコストは,まだ探索しておらず不明であるため, 推定値であるマンハッタン距離$h(S8)=4$を用います(本当は$S8 \rightarrow S12 \rightarrow S13 \rightarrow S9 \rightarrow S10 \rightarrow S17$を辿る必要があり,そのコストは$6$です). よって,$S8$の評価関数は下記のように計算されます.
$$ f(S8) = g(S8)+h(S8) = 4+4 = 8 $$
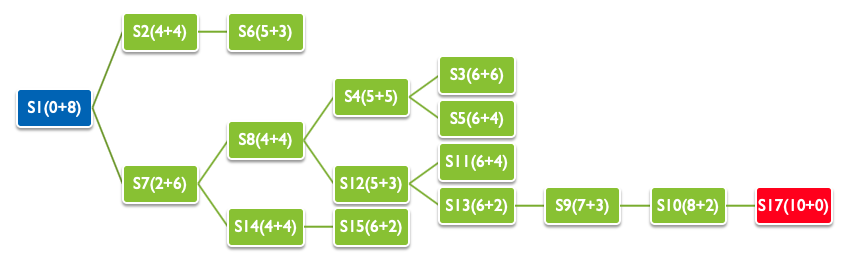
下図は各状態の評価関数$f$を表しています. この値が小さい順番に探索は進行します. A*アルゴリズムの効率は用いるヒューリスティックスに影響されますが, 一般に知識を用いない手法に比べ有効とされています.
実装
最初にライブラリをインポートします.
探索問題の型 を表すSearchPrblem,
A*アルゴリズム のastar ,幅優先探索のbreadth_firstをインポートします.
数値計算ライブラリのnumpyもインポートしておきます.
from simpleai.search import SearchProblem, astar, breadth_first
import numpy as np
最初に各状態の座標を定義します.
S1 = ("S1", 1, 1)
S2 = ("S2", 5, 1)
S3 = ("S3", 2, 2)
S4 = ("S4", 3, 2)
S5 = ("S5", 4, 2)
S6 = ("S6", 5, 2)
S7 = ("S7", 1, 3)
S8 = ("S8", 3, 3)
S9 = ("S9", 4, 3)
S10 = ("S10", 5, 3)
S11 = ("S11", 2, 4)
S12 = ("S12", 3, 4)
S13 = ("S13", 4, 4)
S14 = ("S14", 1, 5)
S15 = ("S15", 3, 5)
S16 = ("S16", 4, 5)
S17 = ("S17", 5, 5)
次に 初期状態 と 目的状態 を定義します. 初期状態は$1$,目的状態は$17$です.
START = S1
GOAL = S17
インポートしたSearchProblemクラスをオーバライドして,
迷路問題を表すMazeProblemを定義します.
オーバライドするメソッドは,actions,result,is_goal,cost,heuristicの5種類です.
class MazeProblem(SearchProblem):
def actions(self, state):
...
def result(self, state, action):
...
def is_goal(self, state):
...
def cost(self, state, action, state2):
...
def heuristic(self, state):
...
actions(self, state)
実行可能な行動のリストを返します. 行動は全部で31パターンが存在します.
def actions(self, state):
list = []
if state == S1:
list = [S2, S7]
if state == S2:
list = [S1, S6]
if state == S3:
list = [S4]
if state == S4:
list = [S3, S5, S8]
if state == S5:
list = [S4]
if state == S6:
list = [S2]
if state == S7:
list = [S1, S8, S14]
if state == S8:
list = [S4, S7, S12]
if state == S9:
list = [S10, S13]
if state == S10:
list = [S9, S17]
if state == S11:
list = [S12]
if state == S12:
list = [S8, S11, S13]
if state == S13:
list = [S9, S12]
if state == S14:
list = [S7, S15]
if state == S15:
list = [S14]
if state == S16:
list = [S17]
if state == S17:
list = [S10, S16]
print(f"{state} -> {list}")
return list
result(self, state, action)
行動actionを,そのまま次の状態として扱います.
def result(self, state, action):
return action
is_goal(self, state)
状態stateがGOALと一致すれば目的状態に達したと判断します.
def is_goal(self, state):
return state == GOAL
cost(self, state, action, state2)
状態間のコストを定義します($g(S)$ではないことに注意). 現在の状態$state$と,遷移先の状態$state2$は, $x$軸または$y$軸に沿って直線的に接続されているため,その座標の差をコストとします. 計算方法は,マンハッタン距離と同じとなりますが, 接続されている状態同士の実際のコストであり,推定値ではないことに注意してください.
def cost(self, state, action, state2):
x1, y1 = state[1], state[2]
x2, y2 = state2[1], state2[2]
c = abs(x1 - x2) + abs(y1 - y2)
return c
heuristic(self, state)
ヒューリスティックス$h(S)$を定義します. 現在の状態$state$から目的状態$GOAL$までのマンハッタン距離です. 上記とは異なり,計算されたコストはあくまで推定値です.
def heuristic(self, state):
x1, y1 = state[1], state[2]
x2, y2 = GOAL[1], GOAL[2]
h = abs(x1 - x2) + abs(y1 - y2)
return h
解の探索
A*アルゴリズムastarを用いて探索します.
探索順番は$S1,S2,S7,\cdots,S5,S10$となっていることがわかります.
problem = MazeProblem(initial_state=START)
result = astar(problem, graph_search=True)
('S1', 1, 1) -> [('S2', 5, 1), ('S7', 1, 3)]
('S2', 5, 1) -> [('S1', 1, 1), ('S6', 5, 2)]
('S7', 1, 3) -> [('S1', 1, 1), ('S8', 3, 3), ('S14', 1, 5)]
('S6', 5, 2) -> [('S2', 5, 1)]
('S8', 3, 3) -> [('S4', 3, 2), ('S12', 3, 4)]
('S14', 1, 5) -> [('S7', 1, 3), ('S15', 3, 5)]
('S12', 3, 4) -> [('S8', 3, 3), ('S11', 2, 4), ('S13', 4, 4)]
('S15', 3, 5) -> [('S14', 1, 5)]
('S13', 4, 4) -> [('S9', 4, 3), ('S12', 3, 4)]
('S4', 3, 2) -> [('S3', 2, 2), ('S5', 4, 2), ('S8', 3, 3)]
('S11', 2, 4) -> [('S12', 3, 4)]
('S9', 4, 3) -> [('S10', 5, 3), ('S13', 4, 4)]
('S5', 4, 2) -> [('S4', 3, 2)]
('S10', 5, 3) -> [('S9', 4, 3), ('S17', 5, 5)]
最終状態,パス,コスト,探索数を確認してみましょう. 初期状態$S1$から目的状態$S17$までのパスは, $S1, S7, S8, S12, S13, S9, S10, S17$であり, そのコストは$10$となっています. ここでのコストはステップ数ではなく, 得られたパスの実際のコスト(距離)となっていることに注意してください.
print(result.state)
print(result.path())
print(result.cost)
('S17', 5, 5)
[(None, ('S1', 1, 1)), (('S7', 1, 3), ('S7', 1, 3)), (('S8', 3, 3), ('S8', 3, 3)), (('S12', 3, 4), ('S12', 3, 4)), (('S13', 4, 4), ('S13', 4, 4)), (('S9', 4, 3), ('S9', 4, 3)), (('S10', 5, 3), ('S10', 5, 3)), (('S17', 5, 5), ('S17', 5, 5))]
10
課題
8パズルを A*アルゴリズム と 幅優先探索 で解き,その探索に掛かる時間を示せ. また,その時間の差について考察せよ.
このとき,初期状態と目的状態は下記に設定すること.
START = (
3, 1, 5,
0, 7, 4,
6, 8, 2
)
GOAL = (
0, 1, 2,
3, 4, 5,
6, 7, 8
)
状態間のコストとヒューリスティックスは下記のように実装する.
costは状態間のコストが常に1であることを表している.
また,heuristicは目的状態と異なるタイルの数をカウントしている.
def cost(self, state, action, state2):
return 1
def heuristic(self, state):
s = np.array(state)
g = np.array(GOAL)
h = 9 - np.sum(s == g)
return h
探索に掛かる時間を計測するには,次のように%timeを用いる.
実行結果のWall timeが探索に掛かった時間である.
problem = EightPuzzle(initial_state=START)
%time result = breadth_first(problem, graph_search=True) # 幅優先探索の時間を計測
problem = EightPuzzle(initial_state=START)
%time result = astar(problem, graph_search=True) # A*の時間を計測
Google Colaboratoryで作成した AI-7.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定