探索アルゴリズム・幅優先探索と深さ優先探索
ノートブックの作成
Google Colaboratory を起動し,新規にノートブックを作成してください. ノートブックのタイトルは AI-6 とします. ノートブックの作成方法は第1回の資料を参照してください.
最初に Simple AI をインストールします. セルで下記のコマンドを実行してください.
!pip install simpleai
迷路問題
今回は 迷路問題 を独自に設計します.
この問題を 状態空間モデル で表現します.
状態空間モデル
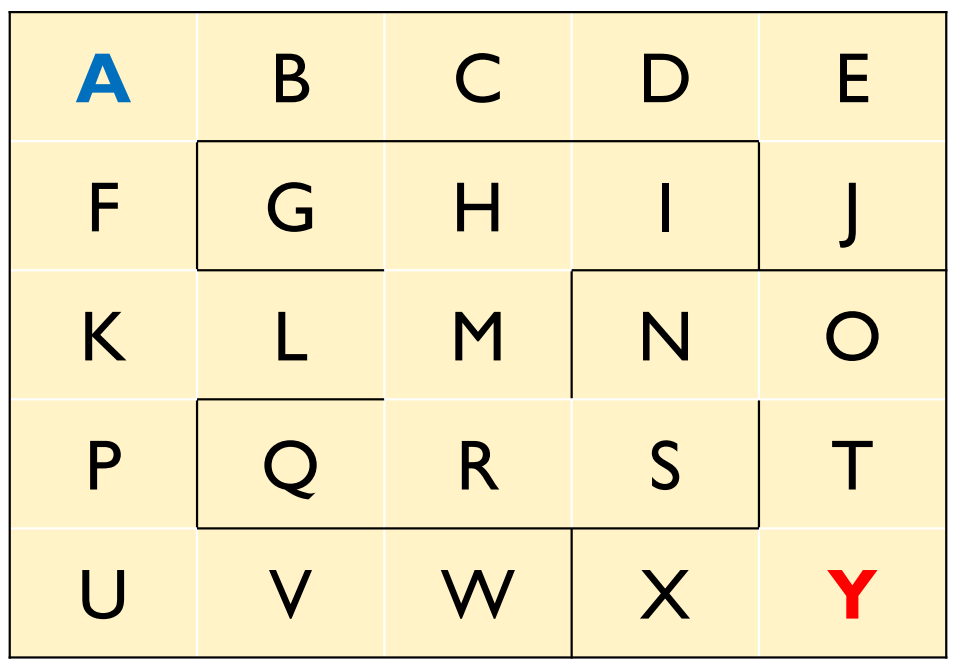
$A$から$Y$までの25の状態から,冗長な状態を取り除く.
例えば,$A \rightarrow B \rightarrow C \rightarrow D \rightarrow E$という経路においては,$B$,$C$,$D$に分岐は存在せず,通り抜けることしかしないため,これらの状態を省略する.
この結果,$S1$から$S17$までの,17通りの状態で問題を表現する.
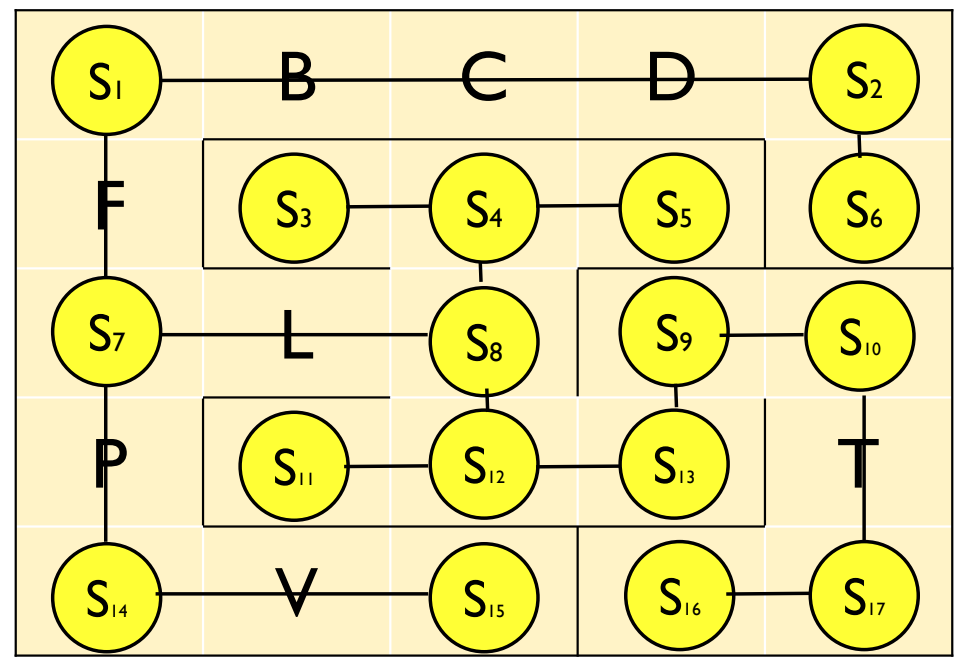 行動は移動可能な状態のペアとして定義する.
例えば,$S1$からは,$S2$と$S7$に移動可能なため,
下記のように表現できる.
行動は移動可能な状態のペアとして定義する.
例えば,$S1$からは,$S2$と$S7$に移動可能なため,
下記のように表現できる.
- $S1 \rightarrow S2$
- $S1 \rightarrow S7$
See the Pen Untitled by Naoto Mukai (@nmukai) on CodePen.
探索アルゴリズム
探索木を用いて初期状態から目的状態を探索するための アルゴリズム(探索する手順) について紹介します. ここでは,ヒューリスティックスと呼ばれる知識を用いないで探索する 幅優先探索 と 深さ優先探索 を取り上げます. これまでに取り上げた,水差し問題,8パズル,ハノイの塔では, 実は幅優先探索を用いていました.
幅優先探索(Breadth First Search)
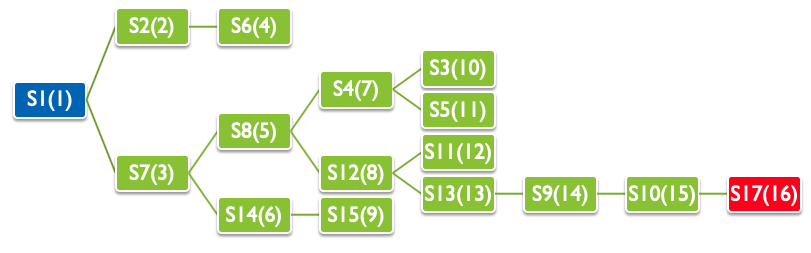
幅優先探索は,探索木の同じ深さの状態を探索してから, 次の深さの状態を探索する手法のことです. ここで,深さ とは初期状態からのコスト(ステップ数)を意味しています. 例えば,上記の迷路問題では,初期状態$S1$から 1ステップで到達可能な$S2$と$S3$を探索します. その次に,2ステップで到達可能な$S6$,$S8$,$S14$を探索します. これを目的状態$S17$に到達するまで繰り返します.
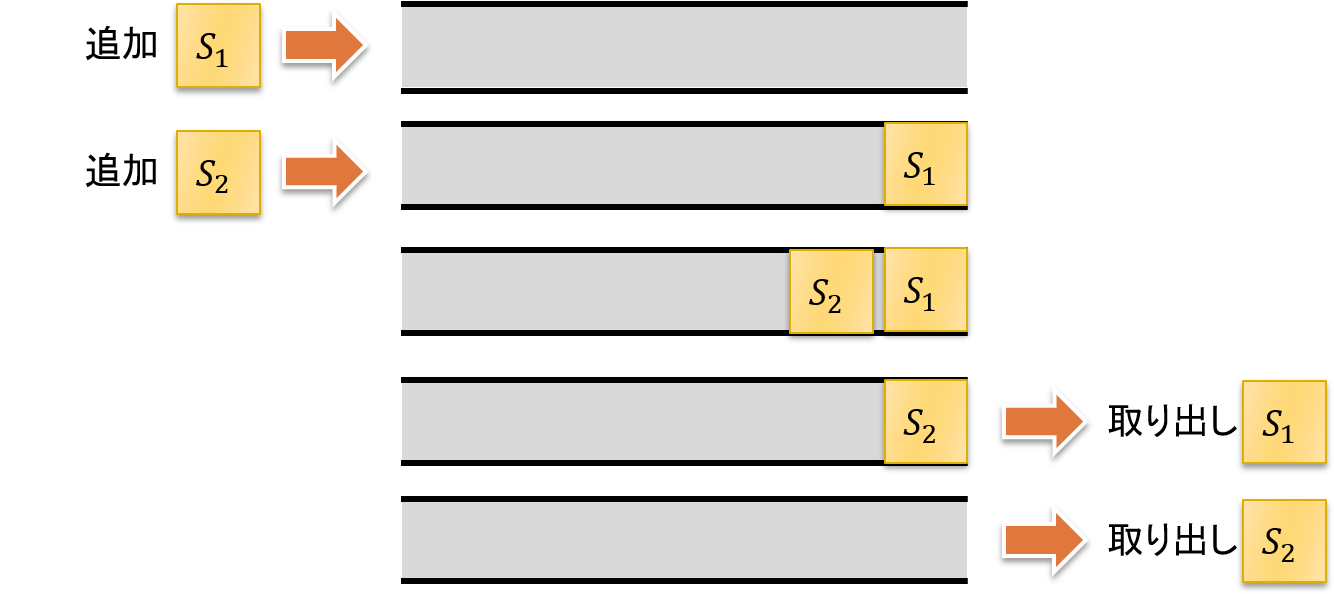
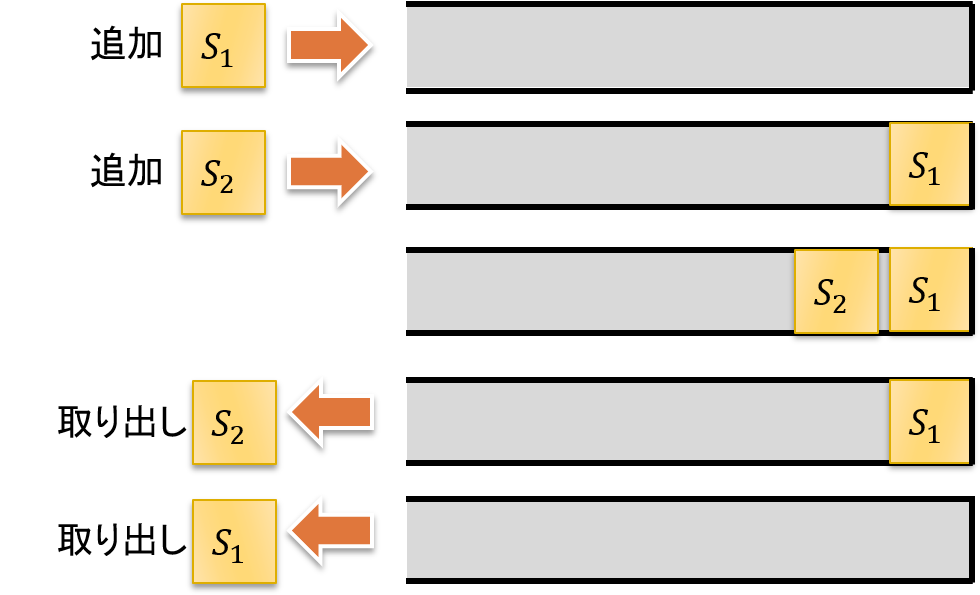
幅優先探索の探索順番は 待ち行列(Queue) で表すことが可能です. 待ち行列を考えるには,下図に示すような,蓋のない筒をイメージします. 筒の左から要素を追加し,筒の右から要素を取り出します. このため「先に入れた要素が,先に取り出される」ことになります. よって,待ち行列は First-In First-Out(FIFO) とも呼ばれます.
今回の迷路問題では,最初に状態$S1$を待ち行列に追加します.
$$ \{ \} \rightarrow \{ S1 \} $$
待ち行列から$S1$を取り出し,$S1$から到達可能な$S2$,$S7$を待ち行列に追加します.
$$ \{ S1 \} \rightarrow \{ S7, S2 \} $$
待ち行列から$S2$を取り出し,$S2$から到達可能な$S6$を待ち行列に追加します.
$$ \{ S7, S2 \} \rightarrow \{ S6, S7 \} $$
待ち行列から$S7$を取り出し,$S7$から到達可能な$S8$と$S14$を待ち行列に追加します.
$$ \{ S6, S7 \} \rightarrow \{ S14, S8, S6 \} $$
このように探索を繰り返すと,$S1$,$S2$,$S7$のように,初期状態に近い状態を優先して探索する 幅優先探索 となります.
深さ優先探索(Depth First Search)
深さ優先探索は,探索木の末端まで探索して目的状態を発見できなければ, 一つ前の分岐まで後戻りして探索する手法のことです. 例えば,上記の迷路問題では,初期状態$S1$から,$S2$,$S6$へと進み, 目的状態が発見できなかったため,$S1$まで戻り,$S7$,$S8$へと探索を進めます. これを目的状態$S17$に到達するまで繰り返します.
深さ優先探索の探索順番は スタック(Stack) で表すことが可能です. スタックを考えるには,下図に示すような,底がある筒をイメージします. 筒の左から要素を追加し,筒の左から要素を取り出します. このため「後に入れた要素が,先に取り出される」ことになります. よって,スタックは Last-In First-Out(LIFO) とも呼ばれます.
今回の迷路問題では,最初に状態$S1$をスタックに追加します.
$$ \{ \} \rightarrow \{ S1 \} $$
スタックから$S1$を取り出し,$S1$から到達可能な$S2$,$S7$をスタックに追加します.
$$ \{ S1 \} \rightarrow \{ S2, S7 \} $$
スタックから$S2$を取り出し,$S2$から到達可能な$S6$をスタックに追加します.
$$ \{ S2, S7 \} \rightarrow \{ S6, S7 \} $$
スタックから$S6$を取り出しますが,$S6$から到達可能な状態はありません.
$$ \{ S6, S7 \} \rightarrow \{ S7 \} $$
このように探索を繰り返すと,$S1$,$S2$,$S6$のように,初期状態から遠い状態を優先して探索する 深さ優先探索 となります.
実装
最初にライブラリをインポートします.
探索問題の型 を表すSearchPrblemと
幅優先探索 を表すbreadth_first,そして,
深さ優先探索 を表すdepth_firstをインポートします.
from simpleai.search import SearchProblem, breadth_first, depth_first
次に 初期状態 と 目的状態 を定義します. 初期状態は$S1$,目的状態は$S17$です.
START = 1
GOAL = 17
インポートしたSearchProblemクラスをオーバライドして,
迷路問題を表すMazeProblemを定義します.
オーバライドするメソッドは,actions,result,is_goalの3種類です.
class MazeProblem(SearchProblem):
def actions(self, state):
...
def result(self, state, action):
...
def is_goal(self, state):
...
actions(self, state)
実行可能な行動のリストを返します. 行動は全部で31パターンが存在します.
def actions(self, state):
list = []
if state == 1: #S1からS2,S7
list = [2, 7]
if state == 2: #S2からS1,S6
list = [1, 6]
if state == 3: #S3からS4
list = [4]
if state == 4: #S4からS3,S5,S8
list = [3, 5, 8]
if state == 5: #S5からS4
list = [4]
if state == 6: #S6からS2
list = [2]
if state == 7: #S7からS1,S8,S14
list = [1, 8, 14]
if state == 8: #S8からS4,S7,S12
list = [4, 7, 12]
if state == 9: #S9からS10,S13
list = [10, 13]
if state == 10: #S10からS9,S17
list = [9, 17]
if state == 11: #S11からS12
list = [12]
if state == 12: #S12からS8,S11,S13
list = [8, 11, 13]
if state == 13: #S13からS9,S12
list = [9, 12]
if state == 14: #S14からS7,S15
list = [7, 15]
if state == 15: #S15からS4
list = [14]
if state == 16: #S16からS17
list = [17]
if state == 17: #S17からS10,S16
list = [10, 16]
print(f"{state} -> {list}")
return list
result(self, state, action)
行動actionを,そのまま次の状態として扱います.
def result(self, state, action):
return action
is_goal(self, state)
状態stateがGOALと一致すれば目的状態に達したと判断します.
def is_goal(self, state):
return state == GOAL
解の探索
幅優先探索
まずは,幅優先探索breadth_firstを用いて探索します.
探索順番は$S1,S2,S7,\cdots,S9,S10$となっており,
初期状態に近い状態を優先して探索していることがわかります.
problem = MazeProblem(initial_state=START)
result = breadth_first(problem, graph_search=True)
1 -> [2, 7]
2 -> [1, 6]
7 -> [1, 8, 14]
6 -> [2]
8 -> [4, 12]
14 -> [7, 15]
4 -> [3, 5, 8]
12 -> [8, 11, 13]
15 -> [14]
3 -> [4]
5 -> [4]
11 -> [12]
13 -> [9, 12]
9 -> [10, 13]
10 -> [9, 17]
最終状態,パス,コストを確認してみましょう. 初期状態$S1$から目的状態$S17$までのパスは, $S1, S7, S8, S12, S13, S9, S10, S17$であり, そのコスト(ステップ数)は$7$となっています.
print(result.state)
print(result.path())
print(result.cost)
17
[(None, 1), (7, 7), (8, 8), (12, 12), (13, 13), (9, 9), (10, 10), (17, 17)]
7
深さ優先探索
次は,深さ先探索depth_firstを用いて探索します.
ここでは,探索順番を揃えるため,actionsの最後を次のように修正します.
行動のリストlistの順番をreverse関数で反転しています(複数の選択肢があるときは若い番号を優先するため).
def actions(self, state):
list = []
...省略...
# この1文を追加
list.reverse() #リストの順番を反転
print(f"{state} -> {list}")
return list
探索順番は$S1,S2,S6,\cdots,S9,S10$となっており, 探索状態が発見できなくなるまで深く探索していることがわかります.
problem = MazeProblem(initial_state=START)
result = depth_first(problem, graph_search=True)
1 -> [7, 2]
2 -> [6, 1]
6 -> [2]
7 -> [14, 8, 1]
8 -> [12, 7, 4]
4 -> [8, 5, 3]
3 -> [4]
5 -> [4]
12 -> [13, 11, 8]
11 -> [12]
13 -> [12, 9]
9 -> [13, 10]
10 -> [17, 9]
最終状態,パス,コストを確認してみましょう. 初期状態$S1$から目的状態$S17$までのパスは, $S1, S7, S8, S12, S13, S9, S10, S17$であり, そのコスト(ステップ数)は$7$となっています. これは幅優先探索と同じ結果です.
print(result.state)
print(result.path())
print(result.cost)
17
[(None, 1), (7, 7), (8, 8), (12, 12), (13, 13), (9, 9), (10, 10), (17, 17)]
7
課題
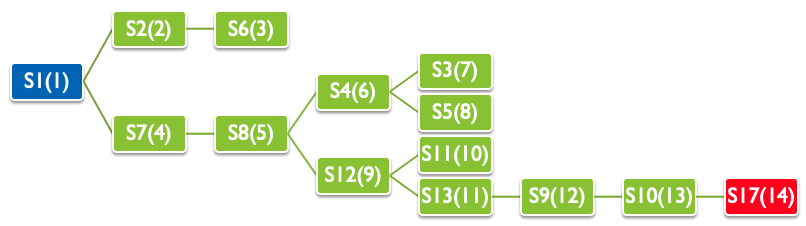
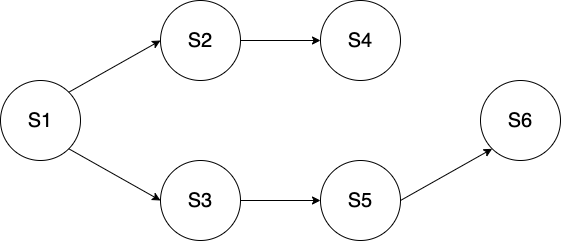
次のネットワークを表す迷路問題を実装し,幅優先探索と深さ優先探索の結果を示せ. また,その差を考察せよ. ただし,初期状態は$S1$,目的状態は$S6$とする.
Google Colaboratoryで作成した AI-6.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定