探索木・「ハノイの塔」
ノートブックの作成
ノートブックのタイトルは AI-5 とします. Google Colaboratory を起動し,新規にノートブックを作成してください. ノートブックの作成方法は第1回の資料を参照してください.
最初に Simple AI をインストールします. セルで下記のコマンドを実行してください.
!pip install simpleai
ハノイの塔
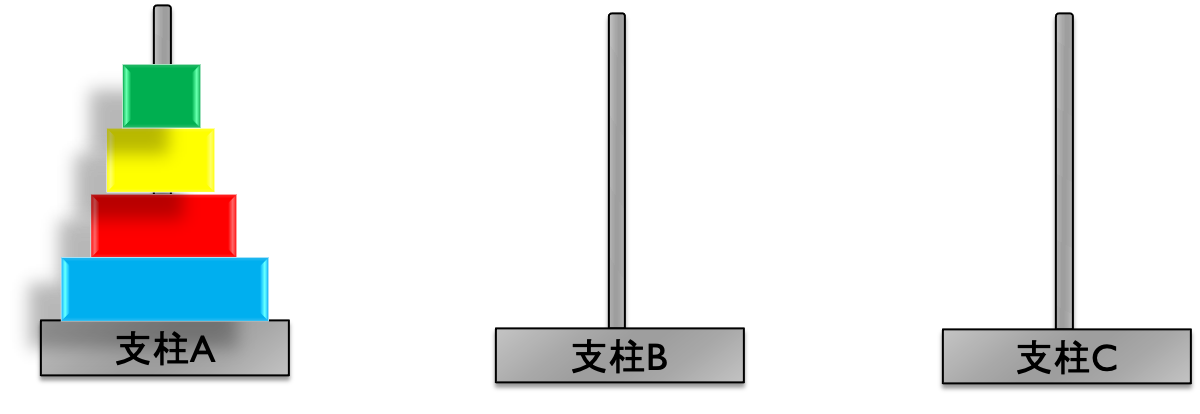
今回は ハノイの塔(Tower of Hanoi) を取り上げましょう.
ハノイの塔
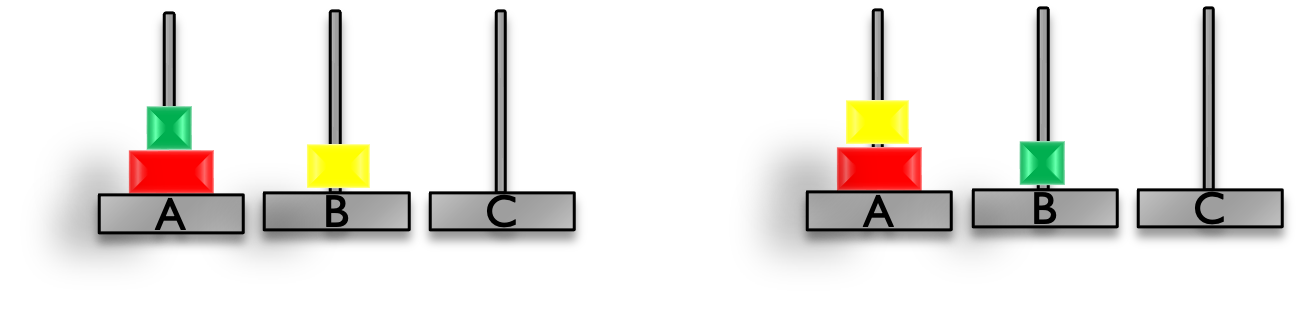
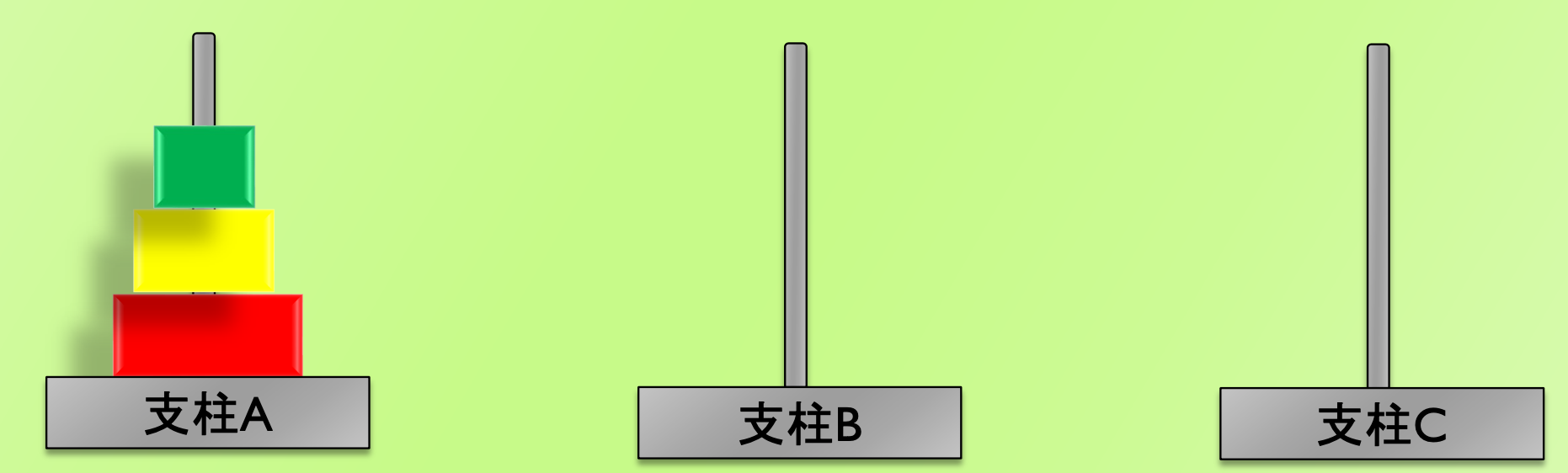
3本の支柱(A,B,C)があり,支柱Aに3枚の円盤(小,中,大)が重なっている.
円盤を他の支柱に移動させることができるが,
必ず大きい円盤の上に小さい円盤が積まれる状態でなければいけない.
支柱Aにある全ての円盤を支柱Cに移すにはどうすれば良いか.
See the Pen Tower of Hanoi by Naoto Mukai (@nmukai) on CodePen.
この問題を 状態空間モデル で表現します. ここでは,モデルAとモデルBの2種類の状態空間モデル検討してみましょう.
モデルAの状態定義
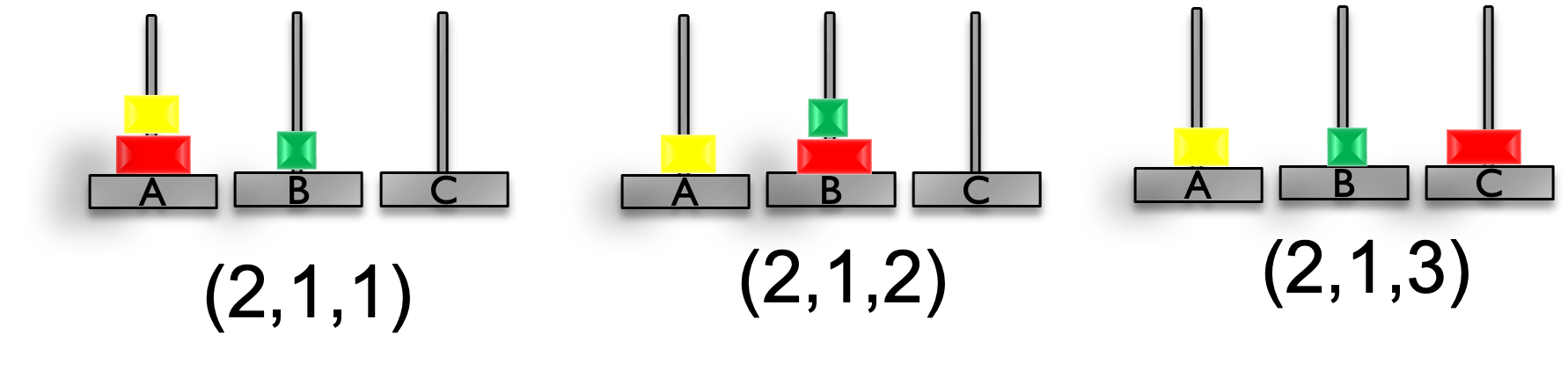
支柱に積まれている円盤の数が1枚のとき1,2枚のとき2,3枚のとき3と表す. この状態を,$(支柱A,支柱B,支柱C)$の順に並べる. 例えば,初期状態は全ての円盤が支柱Aにあるため$(3, 0, 0)$と表す. 同様に,目的状態は全ての円盤が支柱Cにあるため$(0, 0, 3)$と表す. $$ 初期状態:(3, 0, 0) $$ $$ 目的状態:(0, 0, 3) $$
モデルBの状態定義
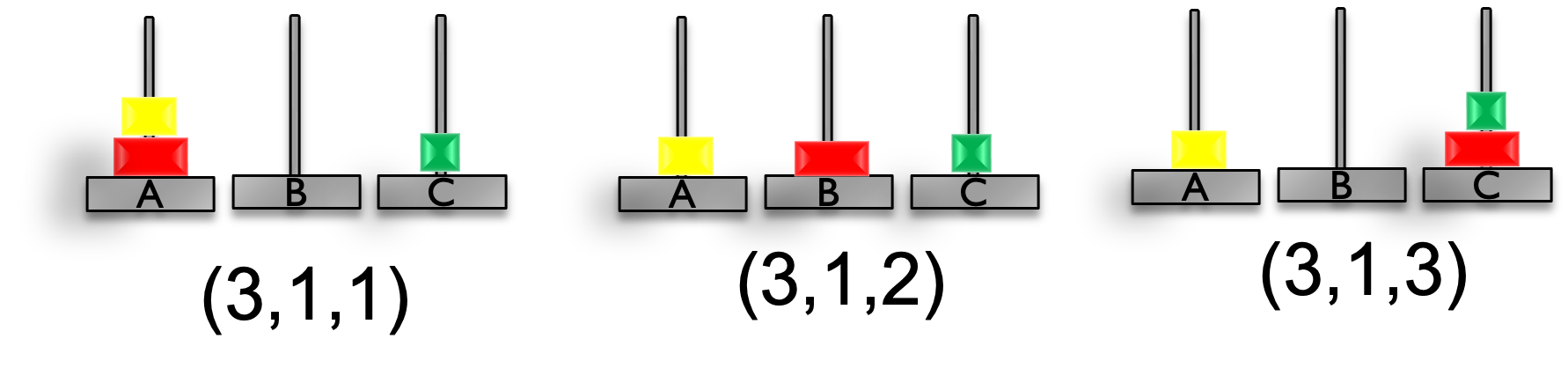
円盤が支柱Aにあるとき1 ,支柱Bにあるとき2, 支柱Cにあるとき3と表す. この状態を,$(円盤(小), 円盤(中), 円盤(大))$の順に並べる. 例えば,初期状態は全ての円盤が支柱Aにあるため$(1, 1, 1)$と表す. 同様に,目的状態は全ての円盤が支柱Cにあるため$(3, 3, 3)$と表す. $$ 初期状態:(1, 1, 1) $$ $$ 目的状態:(3, 3, 3) $$
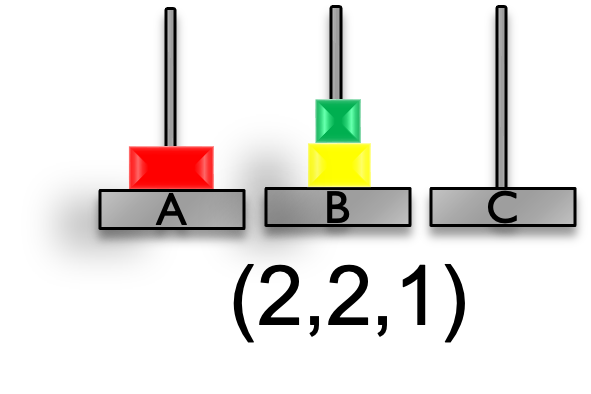
上記のモデルA,モデルBのどちらが適しているでしょうか. 次の2つの状態を例に考えてみましょう. 左の状態は,円盤(小)と円盤(大)が支柱A,円盤(中)が支柱Bにあります. 右の状態は,円盤(中)と円盤(大)が支柱A,円盤(小)が支柱Bにあります. これらを,モデルAとモデルBで表現してみましょう.
| モデル | 左の状態 | 右の状態 |
|---|---|---|
| A | $(2, 1, 0)$ | $(2, 1, 0)$ |
| B | $(1, 2, 1)$ | $(2, 1, 1)$ |
モデルAで表現すると,いずれの状態も$(2, 1, 0)$となって区別できません. これはモデルAが,支柱の位置は表現できる一方で,円盤の大きさを表現できていないことが原因です. 一方,モデルBであれば,支柱の位置と,円盤の大きさの両方を表現できるため,異なる状態として区別することが可能です. よって,ここではハノイの塔の状態空間モデルとして モデルBを採用する ことにします. 次にモデルBの行動を考えましょう.
状態空間モデルBの行動定義
行動(操作)は,円盤を現在の支柱から,他の支柱へ移動することで与えられる.
ただし,大きい円盤を小さい円盤の上に移動させることはできない.
円盤(小)に対する行動は下記の6通りである.
ここで,$y$と$z$は円盤(中)と円盤(大)の状態である.
- A1: $(1, y, z) \rightarrow (2, y, z)$ #支柱Aから支柱Bへ
- A2: $(1, y, z) \rightarrow (3, y, z)$ #支柱Aから支柱Cへ
- A3: $(2, y, z) \rightarrow (1, y, z)$ #支柱Bから支柱Aへ
- A4: $(2, y, z) \rightarrow (3, y, z)$ #支柱Bから支柱Cへ
- A5: $(3, y, z) \rightarrow (1, y, z)$ #支柱Cから支柱Aへ
- A6: $(3, y, z) \rightarrow (2, y, z)$ #支柱Cから支柱Bへ
- A7: $(x, 1, z) \rightarrow (x, 2, z)$ #支柱Aから支柱Bへ
- A8: $(x, 1, z) \rightarrow (x, 3, z)$ #支柱Aから支柱Cへ
- A9: $(x, 2, z) \rightarrow (x, 1, z)$ #支柱Bから支柱Aへ
- A10: $(x, 2, z) \rightarrow (x, 3, z)$ #支柱Bから支柱Cへ
- A11: $(x, 3, z) \rightarrow (x, 1, z)$ #支柱Cから支柱Aへ
- A12: $(x, 3, z) \rightarrow (x, 2, z)$ #支柱Cから支柱Bへ
- A13: $(x, y, 1) \rightarrow (x, y, 2)$ #支柱Aから支柱Bへ
- A14: $(x, y, 1) \rightarrow (x, y, 3)$ #支柱Aから支柱Cへ
- A15: $(x, y, 2) \rightarrow (x, y, 1)$ #支柱Bから支柱Aへ
- A16: $(x, y, 2) \rightarrow (x, y, 3)$ #支柱Bから支柱Cへ
- A17: $(x, y, 3) \rightarrow (x, y, 1)$ #支柱Cから支柱Aへ
- A18: $(x, y, 3) \rightarrow (x, y, 2)$ #支柱Cから支柱Bへ
円盤(小)の行動を適用するための条件
円盤(小)の上に円盤(中),円盤(大)があることはありえないため,常に円盤(小)の全ての行動が適用可能です. 例えば円盤(小)が支柱Aにある場合, 円盤(中)と円盤(大)の位置に関わらず ,常にA1,A2を適用することが可能です.
- A1: $(1, y, z) \rightarrow (2, y, z)$ #支柱Aから支柱Bへ
- A2: $(1, y, z) \rightarrow (3, y, z)$ #支柱Aから支柱Cへ
円盤(中)の行動を適用するための条件
上記の円盤(中)に対する行動に注目してみましょう. 円盤(中)が支柱Aにある場合,候補となる行動は下記の2種類です.
- A7: $(x, 1, z) \rightarrow (x, 2, z)$ #支柱Aから支柱Bへ
- A8: $(x, 1, z) \rightarrow (x, 3, z)$ #支柱Aから支柱Cへ
円盤(小)が支柱Bにあるときは, 円盤(大)の位置に関わらず,行動A8は適用できますが,A7は適用することができません. つまり,$(2, 1, z)$のときは,A8だけが適用可能な行動となります.
円盤(小)が支柱Cにあるときは, 円盤(大)の位置に関わらず,行動A7は適用できますが,A8は適用することができません. つまり,$(3, 1, z)$のときは,A7だけが適用可能な行動となります.
円盤(中)の上に,円盤(小)があるときは,円盤(大)の位置に関わらず,行動A7,A8のいずれも適用することができません. つまり,$(1, 1, z)$のときは,選択可能な行動は存在しないことになります.
円盤(大)の行動を適用するための条件
次に円盤(大)に対する行動に注目してみましょう. 円盤(大)が支柱Aにある場合,候補となる行動は下記の2種類です.
- A13: $(x, y, 1) \rightarrow (x, y, 2)$ #支柱Aから支柱Bへ
- A14: $(x, y, 1) \rightarrow (x, y, 3)$ #支柱Aから支柱Cへ
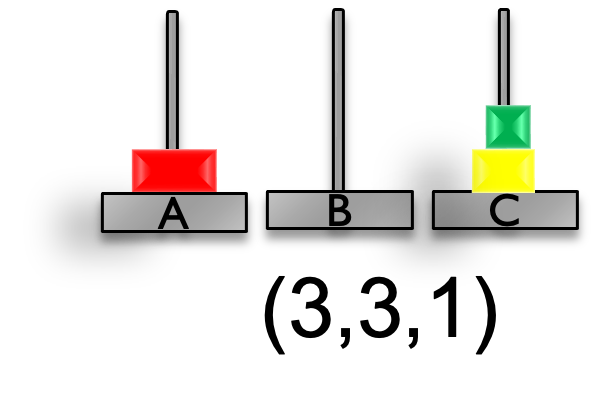
A13が適用な状態は,円盤(小)と円盤(大)が支柱Cにあるときだけです. つまり,$(3, 3, 1)$のときだけ,A13が適用可能です.
A14が適用な状態は,円盤(小)と円盤(大)が支柱Bにあるときだけです. つまり,$(2, 2, 1)$のときだけ,A13が適用可能です.
実装
クラスの定義
最初にライブラリをインポートします.
前回と同様に,探索問題の型 を表すSearchPrblemと
幅優先探索 を表すbreadth_firstをインポートします.
from simpleai.search import SearchProblem, breadth_first
次に 初期状態 と 目的状態 を定義します. 初期状態は$(1, 1, 1)$,目的状態は$(3, 3, 3)$です.
START = (1, 1, 1)
GOAL = (3, 3, 3)
インポートしたSearchProblemクラスをオーバライドして,
ハノイの塔を表すHanoiProblemを定義します.
オーバライドするメソッドは,actions,result,is_goalの3種類です.
class HanoiProblem(SearchProblem):
def actions(self, state):
...
def result(self, state, action):
...
def is_goal(self, state):
...
actions(self, state)
実行可能な行動のリストを返します. 行動は全部で18パターンが存在します. 円盤小は,他の円盤の位置に関係なく移動が可能です. 円盤中は,円盤小が上にない状態で,移動先の支柱に円盤小がなければ移動が可能です. 円盤大は,円盤小と円盤中が上にない状態で,移動先の支柱に円盤小と円盤中がなければ移動が可能です.
def actions(self, state):
actions = []
s = state[0]
m = state[1]
l = state[2]
# 円盤小
if s == 1:
actions.extend(["A1", "A2"])
elif s == 2:
actions.extend(["A3", "A4"])
elif s == 3:
actions.extend(["A5", "A6"])
# 円盤中
if s == 3 and m == 1:
actions.append("A7")
elif s == 2 and m == 1:
actions.append("A8")
elif s == 3 and m == 2:
actions.append("A9")
elif s == 1 and m == 2:
actions.append("A10")
elif s == 2 and m == 3:
actions.append("A11")
elif s == 1 and m == 3:
actions.append("A12")
# 円盤大
if s == 3 and m == 3 and l == 1:
actions.append("A13")
elif s == 2 and m == 2 and l == 1:
actions.append("A14")
elif s == 3 and m == 3 and l == 2:
actions.append("A15")
elif s == 1 and m == 1 and l == 2:
actions.append("A16")
elif s == 2 and m == 2 and l == 3:
actions.append("A17")
elif s == 1 and m == 1 and l == 3:
actions.append("A18")
return actions
result(self, state, action)
行動actionに応じて,円盤を他の支柱に移動させます.
def result(self, state, action):
s = state[0]
m = state[1]
l = state[2]
if action == "A1":
s_ = (2, m, l)
elif action == "A2":
s_ = (3, m, l)
elif action == "A3":
s_ = (1, m, l)
elif action == "A4":
s_ = (3, m, l)
elif action == "A5":
s_ = (1, m, l)
elif action == "A6":
s_ = (2, m, l)
elif action == "A7":
s_ = (s, 2, l)
elif action == "A8":
s_ = (s, 3, l)
elif action == "A9":
s_ = (s, 1, l)
elif action == "A10":
s_ = (s, 3, l)
elif action == "A11":
s_ = (s, 1, l)
elif action == "A12":
s_ = (s, 2, l)
elif action == "A13":
s_ = (s, m, 2)
elif action == "A14":
s_ = (s, m, 3)
elif action == "A15":
s_ = (s, m, 1)
elif action == "A16":
s_ = (s, m, 3)
elif action == "A17":
s_ = (s, m, 1)
elif action == "A18":
s_ = (s, m, 2)
return s_
is_goal(self, state)
状態stateがGOALと一致すれば目的状態に達したと判断します.
def is_goal(self, state):
return state == GOAL
解の探索
幅優先探索(探索木)breadth_firstを用いて解を探索します.
problem = HanoiProblem(initial_state=START)
result = breadth_first(problem, graph_search=True)
探索が終了したら,最終状態,パス,コストを表示します.
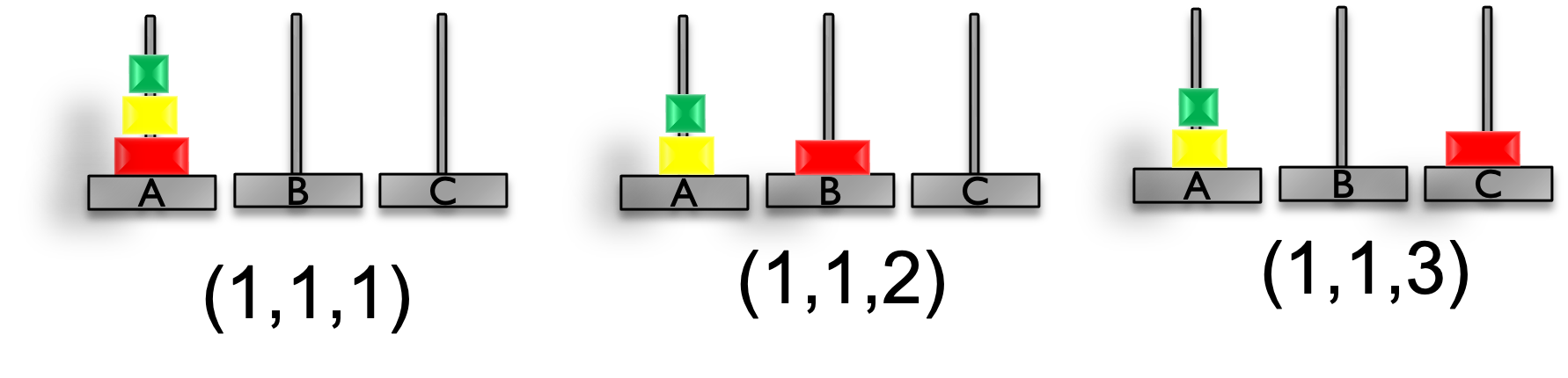
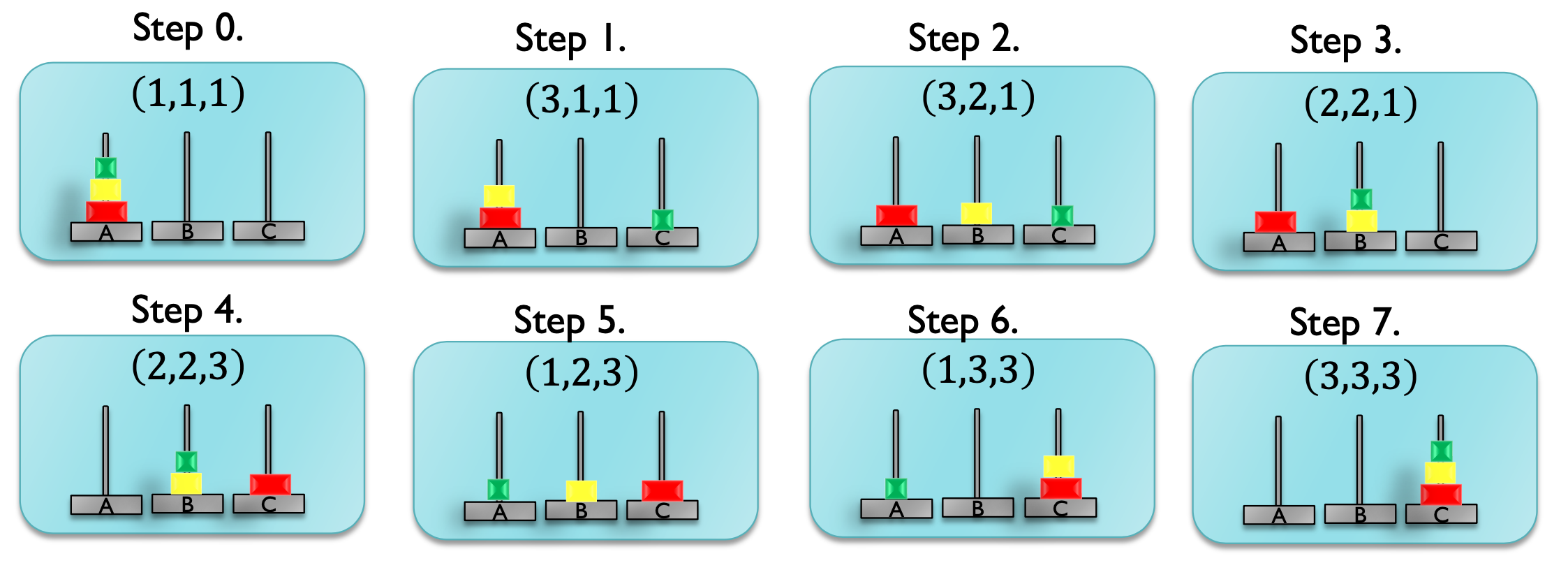
最終状態は(3, 3, 3)となっており目的状態に到達できたことがわかります.
このとき,初期状態から目的状態までのコスト(ステップ数)は7です.
print(result.state)
print(result.path())
print(result.cost)
(3, 3, 3)
[(None, (1, 1, 1)), ('A2', (3, 1, 1)), ('A7', (3, 2, 1)), ('A6', (2, 2, 1)), ('A14', (2, 2, 3)), ('A3', (1, 2, 3)), ('A10', (1, 3, 3)), ('A2', (3, 3, 3))]
7
上記の結果は下図と一致します.
分割統治法
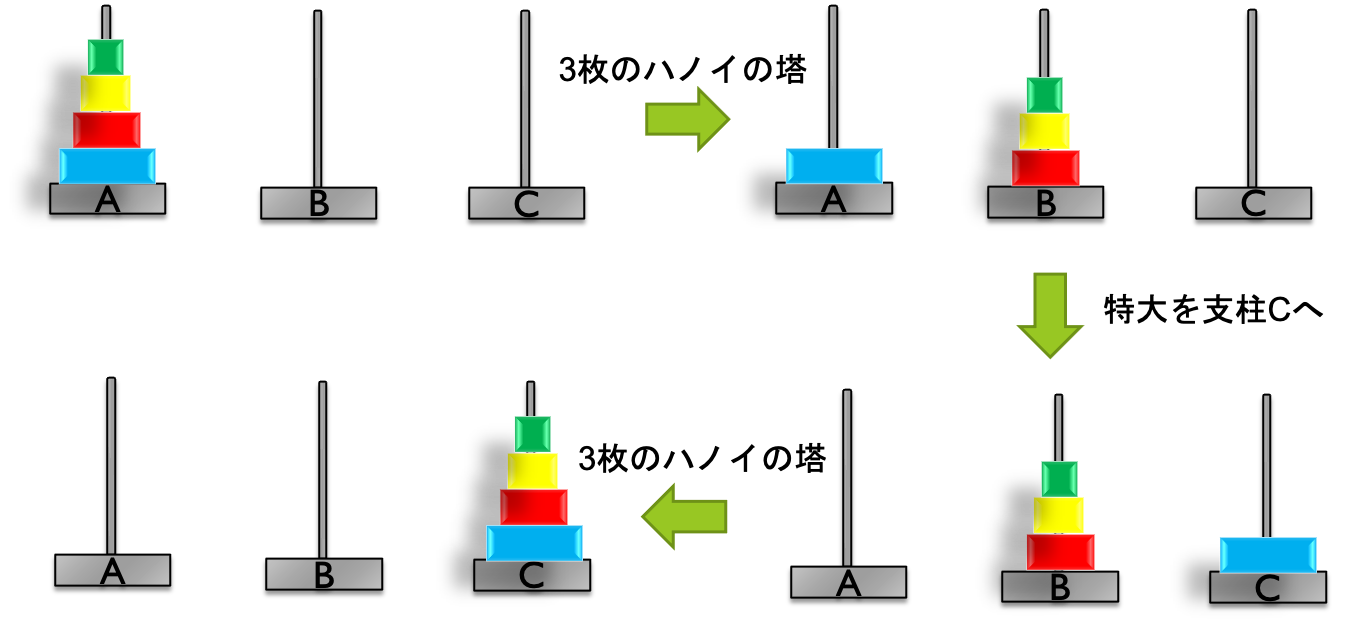
分割統治法 は,大きな問題を小さな問題に分割し,全ての小さな問題の解を導出することで,大きな問題の解を得るという手法です. ハノイの塔は,この分割統治法で効率的に解を導出することが可能です.
例えば,4枚の円盤(小,中,大,特大)のハノイの塔を考えます. 初期状態は$(1,1,1,1)$,目的状態は$(3,3,3,3)$で与えられます.
「4枚の円盤のハノイの塔」は,2つの「3枚の円盤のハノイの塔」に分割することができます.
- 小,中,大の円盤を支柱Bに移動 $(2, 2, 2, 1)$
- 特大の円盤を支柱Cに移動 $(2, 2, 2, 3)$
- 小,中,大の円盤を支柱Cに移動 $(3, 3, 3, 3)$
この手続きを一般化すると,「$n$枚の円盤のハノイの塔」は,「$n-1$枚の円盤のハノイの塔」に分割すれば良いため, 円盤が何枚あっても解を導出することが可能になります. また,ハノイの塔における,円盤の移動回数(コスト)は下記のように表すことが出来ます. ここで,$H(n)$は,$n$枚の円盤のハノイの塔のコストを表します.
ハノイの塔のコスト
$n=1$のときのコストは, $$ H(1) = 1 $$ $n>1$のときのコストは,$n-1$の2回分のコストと,最も大きな円盤の移動コストの和であるため, $$ H(n) = H(n-1) + 1 + H(n-1) = 2 \cdot H(n-1) + 1 $$ よって,次の漸化式が得られる. $$ H(n) + 1 = 2(H(n-1) + 1) $$ 漸化式を解くと,$n$枚のコストは, $$ H(n) = 2^n - 1 $$
課題
下記の初期状態から目的状態まで探索しなさい.
START = (2, 2, 2)
Google Colaboratoryで作成した AI-5.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定