探索木・8パズル

ノートブックの作成

Google Colaboratory を起動し，新規にノートブックを作成してください．ノートブックのタイトルは AI-4 とします．ノートブックの作成方法は第1回の資料を参照してください．

最初に Simple AI をインストールします．セルで下記のコマンドを実行してください．

!pip install simpleai

8パズル

今回は 8パズル（8 Puzzle） を取り上げましょう． 8パズルは，前回の水差し問題に比べ，状態の組み合わせが多く，よい難易度の高い問題であると言えます．水差し問題では，次に示す14通りの状態にしか遷移できません（$(1,1)$などの状態には到達不可能）．

$(0, 0)$ $(0, 1)$ $(0, 2)$ $(0, 3)$ $(0, 4)$ $(1, 0)$ $(1, 4)$ $(2, 0)$ $(2, 4)$ $(3, 0)$ $(3, 1)$ $(3, 2)$ $(3, 3)$ $(3, 4)$

一方で，8パズルはマス目にブランクを含めた9通りのタイルを配置することができるため，状態数は$9!=362,880$通りとなります．この状態空間において，初期状態から目的状態を探索することになります．

$$ 9! = 9 \times 8 \times \cdots \times 1=362880 $$

8パズル

1から8の数字が書いてあるタイルが不規則に3 $\times$ 3のマス目に並べてある．タイルをスライドさせ，左上から順番に1から8まで並び替えるにはどうしたらよいか．

See the Pen Tower of Hanoi by Naoto Mukai (@nmukai) on CodePen.

この問題を 状態空間モデル で表現します．

状態空間モデル

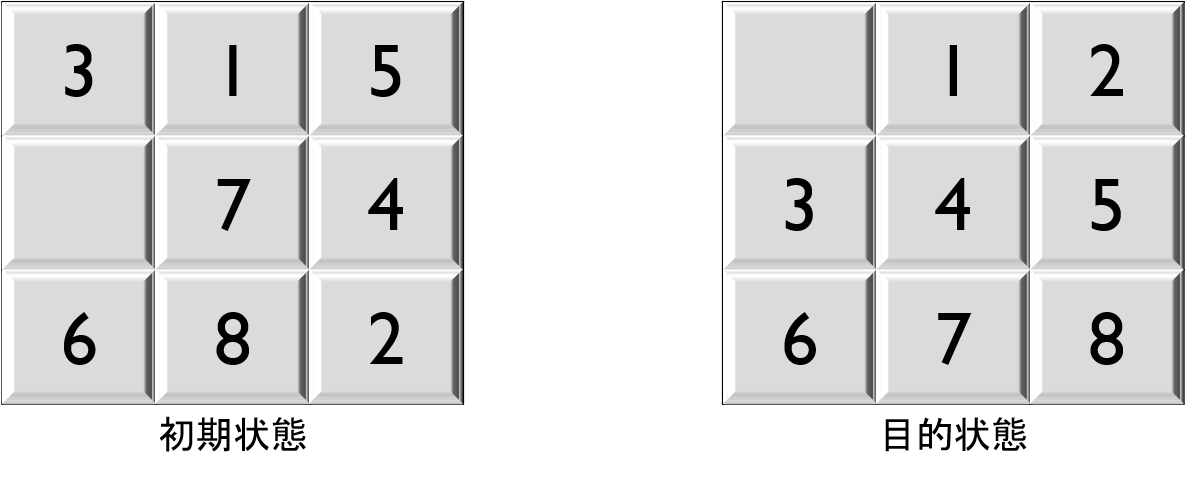
タイルの数字を$x_i$で表す（$i$はタイルの位置）．例えば初期状態と目的状態を下記で与える．タイルがないマスは$b（ブランク）$と表していることに注意すること． $$ 初期状態: (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9) = (3, 1, 5, b, 7, 4, 6, 8, 2) $$ $$ 目的状態: (x_1, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9) = (b, 1, 2, 3, 4, 5, 6, 7, 8) $$ タイルに対する行動（操作）はブランクの位置に応じて決まる．例えば，ブランクが 左上（$x_1$） にあるときは，上（$x_2$）と左（$x_4$）のタイルと入れ替えることができる．

A1: $(b, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9) \rightarrow (x_2, b, x_3, x_4, x_5, x_6, x_7, x_8, x_9)$
A2: $(b, x_2, x_3, x_4, x_5, x_6, x_7, x_8, x_9) \rightarrow (x_4, x_2, x_3, b, x_5, x_6, x_7, x_8, x_9)$

同様に，ブランクが 上（$x_2$） にあるときは，左上（$x_1$），右上（$x_3$），中央（$x_5$）と入れ替えることができます．

A3: $(x_1, b, x_3, x_4, x_5, x_6, x_7, x_8, x_9) \rightarrow (b, x_1, x_3, x_4, x_5, x_6, x_7, x_8, x_9)$
A4: $(x_1, b, x_3, x_4, x_5, x_6, x_7, x_8, x_9) \rightarrow (x_1, x_3, b, x_4, x_5, x_6, x_7, x_8, x_9)$
A5: $(x_1, b, x_3, x_4, x_5, x_6, x_7, x_8, x_9) \rightarrow (x_1, x_5, x_3, x_4, b, x_6, x_7, x_8, x_9)$

上記に沿って全てを列挙すると24の行動が定義できる．

実装

クラスの定義

最初にライブラリをインポートします．前回と同様に，探索問題の型 を表すSearchPrblemと 幅優先探索 を表すbreadth_firstをインポートします．

from simpleai.search import SearchProblem, breadth_first

次に 初期状態 と 目的状態 を定義します．初期状態は$(3, 1, 5, b, 7, 4, 6, 8, 2)$，目的状態は$(b, 1, 2, 3, 4, 5, 6, 7, 8)$です．ここでは，$b$を$0$で表現していることに注意してください．

START = (
    3, 1, 5,
    0, 7, 4,
    6, 8, 2
)

GOAL = (
    0, 1, 2,
    3, 4, 5,
    6, 7, 8
)

インポートしたSearchProblemクラスをオーバライドして， 8パズルを表すEightPuzzleを定義します．オーバライドするメソッドは，actions，result，is_goalの3種類です．

class EightPuzzle(SearchProblem):

    def actions(self, state):
        ...

    def result(self, state, action):
        ...

    def is_goal(self, state):
        ...

actions(self, state)

ブランクの位置に応じた行動のリストを返します．行動は全部で24パターンが存在します．また，状態stateのインデックスは0番から始まることに注意してください．例えば，state[0]は$x_1$を表しています．

def actions(self, state):

  if state[0] == 0: #左上
    actions = ["A1", "A2"]
  if state[1] == 0: #上
    actions = ["A3", "A4", "A5"]
  if state[2] == 0: #右上
    actions = ["A6", "A7"]
  if state[3] == 0: #左
    actions = ["A8", "A9", "A10"]
  if state[4] == 0: #中央
    actions = ["A11", "A12", "A13", "A14"]
  if state[5] == 0: #右
    actions = ["A15", "A16", "A17"]
  if state[6] == 0: #左下
    actions = ["A18", "A19"]
  if state[7] == 0: #下
    actions = ["A20", "A21", "A22"]
  if state[8] == 0: #右下
    actions = ["A23", "A24"]

  return actions

result(self, state, action)

行動actionに応じて，タイルを入れ替えます．例えば，行動A1のときは，左上と上のタイルを入れ替えます．

def result(self, state, action):

	# タプルをリストに変換
    state = list(state)

    if action == "A1": #左上と上を入れ替え
      state[0], state[1] = state[1], state[0]
    elif action == "A2": #左上と左を入れ替え
      state[0], state[3] = state[3], state[0]
    elif action == "A3": #上と左上を入れ替え
      state[1], state[0] = state[0], state[1]
    elif action == "A4": #上と右上を入れ替え
      state[1], state[2] = state[2], state[1]
    elif action == "A5": #上と中央を入れ替え
      state[1], state[4] = state[4], state[1]
    elif action == "A6": #右上と上を入れ替え
      state[2], state[1] = state[1], state[2]
    elif action == "A7": #右上と右を入れ替え
      state[2], state[5] = state[5], state[2]
    elif action == "A8": #左と左上を入れ替え
      state[3], state[0] = state[0], state[3]
    elif action == "A9": #左と中央を入れ替え
      state[3], state[4] = state[4], state[3]
    elif action == "A10": #左と左下を入れ替え
      state[3], state[6] = state[6], state[3]
    elif action == "A11": #中央と上を入れ替え
      state[4], state[1] = state[1], state[4]
    elif action == "A12": #中央と左を入れ替え
      state[4], state[3] = state[3], state[4]
    elif action == "A13": #中央と右を入れ替え
      state[4], state[5] = state[5], state[4]
    elif action == "A14": #中央と下を入れ替え
      state[4], state[7] = state[7], state[4]
    elif action == "A15": #右と右上を入れ替え
      state[5], state[2] = state[2], state[5]
    elif action == "A16": #右と中央を入れ替え
      state[5], state[4] = state[4], state[5]
    elif action == "A17": #右と右下を入れ替え
      state[5], state[8] = state[8], state[5]
    elif action == "A18": #左下と左を入れ替え
      state[6], state[3] = state[3], state[6]
    elif action == "A19": #左下と下を入れ替え
      state[6], state[7] = state[7], state[6]
	elif action == "A20": #下と中央を入れ替え
      state[7], state[4] = state[4], state[7]
    elif action == "A21": #下と左下を入れ替え
      state[7], state[6] = state[6], state[7]
    elif action == "A22": #下と右下を入れ替え
      state[7], state[8] = state[8], state[7]
    elif action == "A23": #右下と右を入れ替え
      state[8], state[5] = state[5], state[8]
    elif action == "A24": #右下と下を入れ替え
      state[8], state[7] = state[7], state[8]

	# リストをタプルに変換
    return tuple(state)

is_goal(self, state)

状態stateがGOALと一致すれば目的状態に達したと判断します．

def is_goal(self, state):
    return state == GOAL

解の探索

幅優先探索（探索木）breadth_firstを用いて解を探索します．

problem = EightPuzzle(initial_state=START)
result = breadth_first(problem, graph_search=True)

探索が終了したら，最終状態，パス，コストを表示します．最終状態は(0, 1, 2, 3, 4, 5, 6, 7, 8)となっており目的状態に到達できたことがわかります．このとき，初期状態から目的状態までのコスト（ステップ数）は13です．

print("State:", result.state)
print("Path:", result.path())
print("Cost:", result.cost)

State: (0, 1, 2, 3, 4, 5, 6, 7, 8)
Path: [(None, (3, 1, 5, 0, 7, 4, 6, 8, 2)), ('A8', (0, 1, 5, 3, 7, 4, 6, 8, 2)), ('A1', (1, 0, 5, 3, 7, 4, 6, 8, 2)), ('A4', (1, 5, 0, 3, 7, 4, 6, 8, 2)), ('A7', (1, 5, 4, 3, 7, 0, 6, 8, 2)), ('A17', (1, 5, 4, 3, 7, 2, 6, 8, 0)), ('A24', (1, 5, 4, 3, 7, 2, 6, 0, 8)), ('A20', (1, 5, 4, 3, 0, 2, 6, 7, 8)), ('A11', (1, 0, 4, 3, 5, 2, 6, 7, 8)), ('A4', (1, 4, 0, 3, 5, 2, 6, 7, 8)), ('A7', (1, 4, 2, 3, 5, 0, 6, 7, 8)), ('A16', (1, 4, 2, 3, 0, 5, 6, 7, 8)), ('A11', (1, 0, 2, 3, 4, 5, 6, 7, 8)), ('A3', (0, 1, 2, 3, 4, 5, 6, 7, 8))]
Cost: 13

探索木（解の探索過程）

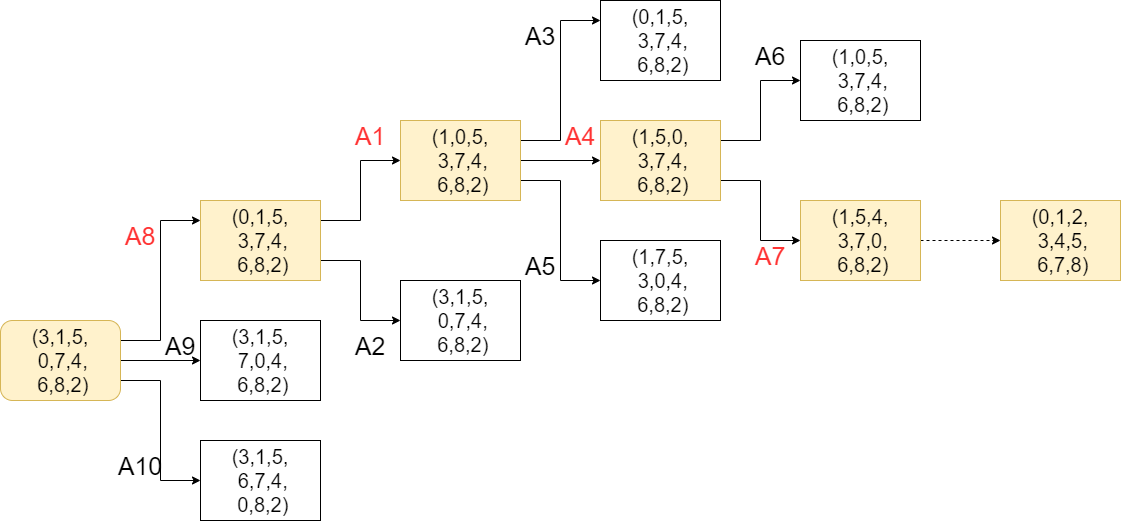
8パズルの探索木は次の図のようになります．初期状態(3, 1, 5, 0, 7, 4, 6, 8, 2)から目的状態(0, 1, 2, 3, 4, 5, 6, 7, 8)までの探索過程は次の図で表すことができます．初期状態(3, 1, 5, 0, 7, 4, 6, 8, 2)は，左にブランクがあるため，適用可能な行動は，A8，A9，A10のいずれかです． A8を適用すると，左と左上を交換するため，状態は(0, 1, 5, 3, 7, 4, 6, 8, 2)になります． A9を適用すると，左と中央を交換するため，状態は(3, 1, 5, 7, 0, 4, 6, 8, 2)になります． A10を適用すると，左と左下を交換するため，状態は(3, 1, 5, 6, 7, 4, b, 8, 2)になります．この新しく生成された状態に対し，さらに適用可能な行動を繰り返し，目的状態(0, 1, 2, 3, 4, 5, 6, 7, 8)に到達すると探索は終了です．水差し問題では探索した状態数が 12 であったことに対し，8パズルで探索した状態数は 2115 となり，探索空間が大きくなっていることがわかります．

課題

下記の初期状態から目的状態まで探索しなさい．

START = (
    1, 5, 0,
    3, 7, 4,
    6, 8, 2
)

Google Colaboratoryで作成した AI-4.ipynb を保存し， ノートブック（.ipynb） をダウンロードして提出しなさい．提出の前に必ず下記の設定を行うこと．

ノートブックの設定で「セルの出力を除外する」のチェックを外す
ノートブックの変更内容を保存して固定

Top Back

愛知県名古屋市にある椙山女学園大学文化情報学部向研究室の公式サイトです．専門は情報科学であり，人工知能やデータベースなどの技術要素を指導しています．この公式サイトでは，授業で使用している教材を公開すると共に，ベールに包まれた女子大教員のミステリアスな日常を４コマ漫画でお伝えしていきます．サイトに関するご意見やご質問はFacebookまたはTwitterでお問い合わせください．