探索木・ゲーム木
ゲーム木
これまでは8パズルやハノイの塔など1人のプレイヤーが解く問題を対象にしていました. ここでは,プレイヤーとコンピュータが対戦するオセロや将棋などの対戦形式のゲームについて考えましょう.
人間とコンピュータとの対戦
対戦形式のゲームは,従来から人工知能の研究テーマとして取り組まれています. これまでに,人間(プロ棋士)とコンピュターとの対戦がメディアにも取り上げられています. 1997年には,IBMのDeep Blueが当時のチェスのチャンピオンに勝利しました, 2013年には,山本一成氏が開発したPonanzaがプロ棋士に勝利したことが注目されました. さらに,2016年には,ディープラーニングを取り入れたDeepMindのAlphaGoがプロ棋士に勝利しました. このように,対戦形式のゲームでは,既にコンピュータ(AI)が人間を超えるようになっています.
| ゲーム | 年 | 状況 |
|---|---|---|
| オセロ | 1980年 | ムーアが世界チャンピオンの井上博に勝利 |
| チェス | 1997年 | IBMのDeepBlueが世界チャンピオンのガルリ・カスパロフに勝利 |
| 将棋 | 2013年 | 山本一成が開発したPonanzaがプロ棋士の佐藤慎一に勝利 |
| 囲碁 | 2016年 | DeepMindのAlphaGoがプロ棋士のイ・セドルに勝利 |
ゲーム木を利用した解の導出
対戦形式のゲームでは,プレイヤーの選択と,コンピュータの選択が交互に繰り返されます. このため,これまでの探索木では,適切な解を導出することができません. このような場合, ゲーム木(Game Tree) と呼ばれる手法が用いられます.
ゲーム木は次のような木構造で表されます.
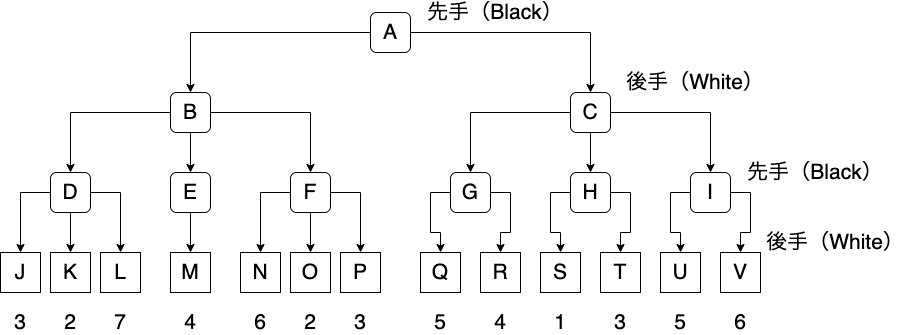
木のルート(根)であるAはゲームの初期状態(盤面)であり,先手(黒)が手を打つ場面です.
先手が手を打つとBまたはCに遷移します.
BとCは後手(白)が手を打つ場面です.
同様に,後手が手を打つと,BからD,E,F,また,CからG,H,I,のいずれかに遷移します.
DからIは先手が手を打つ場面です.
最終的には,後手が手を打つ場面であるJからVに遷移します.
JからVの状態(盤面)には,先手がどれぐらい有利かを表す評価が与えられます
(評価を決める評価関数はゲームによって異なり,開発者が最も頭を悩ませる部分です).
例えば,Jは3,Kは2,Lは7となっています.
先手にとっては,A - B - D - Lと遷移すると,最も評価の高い 7 になりますが,
後手は先手の評価を下げようと手を打つため,実際はLに到達することはできません.
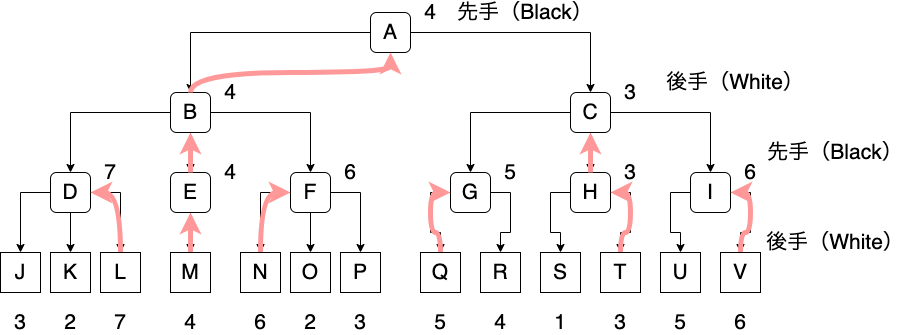
そこで,ミニマックス法(minimax) を用いて解を導出します.
先手は評価を 最大化 ,後手は評価を 最小化 することから名付けられました.
Dの場面では,先手が手を打つため,評価が最大となるLを選択します.
よって,Dの評価もLと同じ7に設定します.
同様に,EからIの評価も設定します.
Bの場面では,後手が手を打つため,評価が最小となるEを選択します.
よって,Bの評価もEと同じ4に設定します.
同様に,Cの評価は3に設定されます.
Aの場面では,先手が手を打つため,評価が最大なるBを選択します.
よって,Aの評価はBと同じ4に設定されます.
このため,A - B - E - Mに遷移することが先手にとって最良の選択となります.
1手ごとにミニマックス法による探索を実行し,先手は次の1手を決めます. 先の例では深さが3までの探索でした(先手 - 後手 - 先手 - 後手). これを深くすることで,より有利な手を導出することができます. しかし,探索する状態の組み合わせが爆発的に増加するため,効率良く探索することが求められます( アルファベータ法 など).
ノートブックの作成
Jupyter Notebook を起動し,新規にノートブックを作成してください. ノートブックのタイトルは AI-17 とします. ノートブックの作成方法は第1回の資料を参照してください.
最初に木構造を表現するtreelibをインストールします. treelibはゲーム木を表現するために用います. セルで下記のコマンドを実行してください.
> !pip install treelib
また,treelibに加え,下記のライブラリも導入しておきましょう.
from treelib import Node, Tree
import numpy as np
import itertools
実装
ゲーム木を実装してみましょう.
最初に状態(盤面)の評価を表す Evaluationクラスを定義します.
Evaluationクラスは,「プレイヤー(先手または後手)」,「盤面の状態」,「盤面の評価」を保持します.
# 盤面の評価
class Evaluation():
# 初期化
def __init__(self, player, board, value):
self.player = player #プレイヤー
self.board = board # 状態
self.value = value # 評価
self.text = self.__str__()
# 文字列化
def __str__(self):
return f"[{self.player} {self.board} {self.value}]"
# 評価の更新
def update(self, value):
self.value = value
self.text = self.__str__()
treelibでゲーム木を表現します.
先手はBlack,後手はWhiteで表現しています.
また,盤面の状態は,先の図に合わせて,AからVとしています(本来は駒の配置などを表現する).
盤面の評価も,先の図と同じ値に設定しています(本来は評価関数で計算する).
# ゲーム木
tree = Tree()
# Blackの盤面(先手)
tree.create_node("A", "A", data=Evaluation("Black", "A", None))
# Whiteの盤面(後手)
tree.create_node("B", "B", data=Evaluation("White", "B", None), parent="A")
tree.create_node("C", "C", data=Evaluation("White", "C", None), parent="A")
# Blackの盤面(先手)
tree.create_node("D", "D", data=Evaluation("Black", "D", None), parent="B")
tree.create_node("E", "E", data=Evaluation("Black", "E", None), parent="B")
tree.create_node("F", "F", data=Evaluation("Black", "F", None), parent="B")
tree.create_node("G", "G", data=Evaluation("Black", "G", None), parent="C")
tree.create_node("H", "H", data=Evaluation("Black", "H", None), parent="C")
tree.create_node("I", "I", data=Evaluation("Black", "I", None), parent="C")
# Whiteの盤面(後手)
# 評価は先手にとっての盤面の価値を表すことに注意
tree.create_node("J", "J", data=Evaluation("White", "J", 3), parent="D")
tree.create_node("K", "K", data=Evaluation("White", "K", 2), parent="D")
tree.create_node("L", "L", data=Evaluation("White", "L", 7), parent="D")
tree.create_node("M", "M", data=Evaluation("White", "M", 4), parent="E")
tree.create_node("N", "N", data=Evaluation("White", "N", 6), parent="F")
tree.create_node("O", "O", data=Evaluation("White", "O", 2), parent="F")
tree.create_node("P", "P", data=Evaluation("White", "P", 3), parent="F")
tree.create_node("Q", "Q", data=Evaluation("White", "Q", 5), parent="G")
tree.create_node("R", "R", data=Evaluation("White", "R", 4), parent="G")
tree.create_node("S", "S", data=Evaluation("White", "S", 1), parent="H")
tree.create_node("T", "T", data=Evaluation("White", "T", 3), parent="H")
tree.create_node("U", "U", data=Evaluation("White", "U", 5), parent="I")
tree.create_node("V", "V", data=Evaluation("White", "V", 6), parent="I")
作成したゲーム木を表示します.
末端以外の状態の評価はNoneとなっていることに注意してください.
先の図と同じ木構造になっていることを確認できます.
# ゲーム木の表示
tree.show(data_property="text")
[Black A None]
├── [White B None]
│ ├── [Black D None]
│ │ ├── [White J 3]
│ │ ├── [White K 2]
│ │ └── [White L 7]
│ ├── [Black E None]
│ │ └── [White M 4]
│ └── [Black F None]
│ ├── [White N 6]
│ ├── [White O 2]
│ └── [White P 3]
└── [White C None]
├── [Black G None]
│ ├── [White Q 5]
│ └── [White R 4]
├── [Black H None]
│ ├── [White S 1]
│ └── [White T 3]
└── [Black I None]
├── [White U 5]
└── [White V 6]
ミニマックス法で,木の末端から評価を伝播させて,全ての状態(盤面)の評価を設定します. 深さが奇数のときは最大値を選択し,偶数のときは最小値を選択します.
# ミニマックス法
def minimax(tree):
# ノードを取得
nodes = tree.all_nodes()
# 降順で並べ替え
nodes = sorted(nodes, key=lambda x: tree.depth(x), reverse=True)
for node in nodes:
if not(node.is_root()):
parent = tree.parent(node.identifier) # 親ノード
depth = tree.depth(node) # 深さ
if depth % 2 == 1:
if parent.data.value:
# 最大値を選択
parent.data.update(max(parent.data.value, node.data.value))
else:
parent.data.update(node.data.value)
else:
if parent.data.value:
# 最小値を選択
parent.data.update(min(parent.data.value, node.data.value))
else:
parent.data.update(node.data.value)
return tree
再度,ゲーム木を表示します. 全ての状態(盤面)に評価が設定されていることがわかります.
tree = minimax(tree)
tree.show(data_property="text")
[Black A 4]
├── [White B 4]
│ ├── [Black D 7]
│ │ ├── [White J 3]
│ │ ├── [White K 2]
│ │ └── [White L 7]
│ ├── [Black E 4]
│ │ └── [White M 4]
│ └── [Black F 6]
│ ├── [White N 6]
│ ├── [White O 2]
│ └── [White P 3]
└── [White C 3]
├── [Black G 5]
│ ├── [White Q 5]
│ └── [White R 4]
├── [Black H 3]
│ ├── [White S 1]
│ └── [White T 3]
└── [Black I 6]
├── [White U 5]
└── [White V 6]
先手はBまたはCの評価の高い方を選択します.
ここでは,評価4のBが選択されることになります.
この選択を1手ごとに繰り返します.
def getMax(tree):
# 降順で並べ替え
nodes = tree.children(tree.root)
nodes = sorted(nodes, key=lambda x: x.data.value, reverse=True)
# 評価が最大の状態を選択
max_node = nodes[0]
return max_node
max_node = getMax(tree)
print(max_node.data)
[White B 4]
課題
Google Colaboratoryで作成した AI-17.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定