遺伝的アルゴリズム・巡回セールスマン問題
ノートブックの作成
Google Colaboratory を起動し,新規にノートブックを作成してください. ノートブックのタイトルは AI-11 とします. ノートブックの作成方法は第1回の資料を参照してください.
最初に Simple AI と NetworkX をインストールします. NetworkXはネットワーク分析のためのライブラリです. セルで下記のコマンドを実行してください.
!pip install simpleai
!pip install network
巡回セールスマン問題
今回は 巡回セールスマン問題(Traveling Salesman Problem) を取り上げましょう.
巡回セールスマン問題
$A,B,C,D,E,F,G,H,I,J$で表される10の都市がある. 各都市の座標は次の表で与えられる.
| 都市 | A | B | C | D | E | F | G | H | I | J |
|---|---|---|---|---|---|---|---|---|---|---|
| X | 17 | 97 | 32 | 63 | 57 | 83 | 100 | 12 | 3 | 55 |
| Y | 72 | 8 | 15 | 97 | 60 | 48 | 26 | 62 | 49 | 77 |
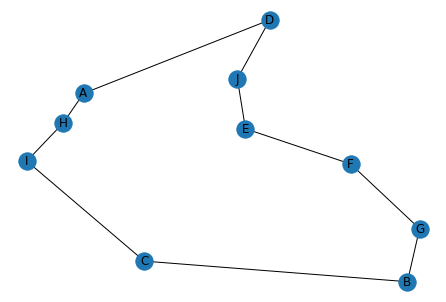
都市ネットワーク
10都市を巡る巡回路を,NetworkXライブラリを利用して,ネットワーク(グラフ)として表現します.
都市はnodes,経路はrouteで表します.
このとき,都市の座標は辞書型の pos に設定します.
また,経路は2都市間のタプル("A","B")を繋げて表現します.
import networkx as nx
import numpy as np
import random
import copy
from simpleai.search import SearchProblem
from simpleai.search.local import genetic
# グラフの初期化
graph = nx.Graph()
# ノード
nodes = ["A", "B", "C", "D", "E", "F", "G", "H", "I", "J"]
# ノードの位置
pos ={
"A": (17, 72),
"B": (97, 8),
"C": (32, 15),
"D": (63, 97),
"E": (57, 60),
"F": (83, 48),
"G": (100, 26),
"H": (12, 62),
"I": (3, 49),
"J": (55, 77)
}
# 経路
route = [("A", "B"), ("B", "C"), ("C", "D"), ("D", "E"), ("E", "F"), ("F", "G"), ("G", "H"), ("H", "I"), ("I", "J"), ("J", "A")]
graph.add_edges_from(route)
# 描画
nx.draw(graph, pos=pos, with_labels=True)
遺伝的アルゴリズム
前回に引き続き,巡回セールスマン問題を 遺伝的アルゴリズム(Genetic Algorithm) で解くことに挑戦します. まずは,巡回セールスマン問題における遺伝的アルゴリズムの個体(遺伝子)の定義を考えます.
都市を回る順番をそのまま個体として表現することを考えます. 例えば,$A,B,\cdots,E$の5つの都市の巡回路において,$1,2, \cdots, 5$の数字を割り当て, この数字の列を個体とする方法です.
$$ A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow A $$
$$ I_1 = (1, 2, 3, 4, 5) $$
$$ A \rightarrow D \rightarrow E \rightarrow B \rightarrow C \rightarrow A $$
$$ I_2 = (1, 4, 5, 2, 3) $$
この方法では,$I_1$と$I_2$に交叉を適用したとき,巡回路の条件を満たさない解が得られることがあります(致死解). 例えば,上記の$I_1$と$I_2$の3番目の遺伝子から交叉する場合を考えます. 同じ都市を2回訪れる経路や,全ての都市を巡らない経路が生成されることがわかります.
$$ A \rightarrow B \rightarrow E \rightarrow B \rightarrow C \rightarrow A $$
$$ I_{1}^{'} = (1, 2, 5, 2, 3) $$
$$ A \rightarrow D \rightarrow C \rightarrow D \rightarrow E \rightarrow A $$
$$ I_{2}^{'} = (1, 4, 3, 4, 5) $$
そこで,次のように個体を表現することにします.
この方法では,訪れる都市が,$A, B, C, D, E$の何番目にあるかを表します.
例えば,最初に訪れる都市が$A$であれば,$A$は$A, B, C, D, E$の0番目にあるため,遺伝子は0とします.
次に訪れる都市が$D$であれば,$D$は$B, C, D, E$の2番目にあるため,遺伝子は2とします.
この方法では致死解は生じません.
$$ A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow A $$
$$ I_{1}^{'} = (0, 0, 0, 0, 0) $$
| 訪問する都市 | 都市の順番 | 遺伝子 |
|---|---|---|
| A | ABCDE | 0 |
| B | BCDE | 0 |
| C | CDE | 0 |
| D | DE | 0 |
| E | E | 0 |
$$ A \rightarrow D \rightarrow E \rightarrow B \rightarrow C \rightarrow A $$
$$ I_2 = (0, 2, 2, 0, 0) $$
| 訪問する都市 | 都市の順番 | 遺伝子 |
|---|---|---|
| A | ABCDE | 0 |
| D | BCDE | 2 |
| E | BCE | 2 |
| B | BC | 0 |
| C | C | 0 |
上記の方法に従って,経路から個体(遺伝子)を生成するtoGene()を定義します.
初期経路の個体が$(0, 0, 0, 0, 0, 0, 0, 0, 0, 0)$となっていることがわかります.
# 経路から個体(遺伝子)へ
def toGene(route):
destinations = list(copy.deepcopy(graph.nodes))
gene = []
for edge in route:
index = destinations.index(edge[0])
destinations.pop(index)
gene.append(index)
return gene
gene = toGene(route)
print(gene)
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
逆に個体(遺伝子)から経路を生成するtoRoute()を定義します.
個体に対応する経路が下記であることがわかります.
$$ A \rightarrow B \rightarrow C \rightarrow D \rightarrow E \rightarrow F \rightarrow G \rightarrow H \rightarrow I \rightarrow J \rightarrow A $$
# 個体(遺伝子)から経路へ
def toRoute(gene):
destinations = list(copy.deepcopy(graph.nodes))
nodes = []
for index in gene:
node = destinations[index]
destinations.pop(index)
nodes.append(node)
route = []
for i, node in enumerate(nodes):
edge = ((nodes[i], nodes[(i+1) % len(nodes)]))
route.append(edge)
return route
route = toRoute(gene)
print(route)
[('A', 'B'), ('B', 'C'), ('C', 'D'), ('D', 'E'), ('E', 'F'), ('F', 'G'), ('G', 'H'), ('H', 'I'), ('I', 'J'), ('J', 'A')]
ランダムに個体を生成するrandomGene()を定義します.
生成された個体と対応する経路を合わせて確認しておきます.
# ランダムに個体を生成
def randomGene():
destinations = list(copy.deepcopy(graph.nodes))
gene = []
for i in range(len(destinations)):
node = random.choice(destinations)
index = destinations.index(node)
destinations.pop(index)
gene.append(index)
return gene
gene = randomGene()
print(gene)
print(toRoute(gene))
[9, 4, 4, 6, 0, 2, 1, 2, 1, 0]
[('J', 'E'), ('E', 'F'), ('F', 'I'), ('I', 'A'), ('A', 'D'), ('D', 'C'), ('C', 'H'), ('H', 'G'), ('G', 'B'), ('B', 'J')]
巡回セールスマン問題の目的関数となる経路コストを算出するdistance()を定義します.
この経路コストを 最小化 することが目的となります.
# 経路距離
def distance(route):
d = 0
for edge in route:
pos_head = np.array(pos[edge[0]])
pos_tail = np.array(pos[edge[1]])
d += np.linalg.norm(pos_tail - pos_head)
return d
d = distance(route)
print(f"distance={d}")
distance=557.6889363201603
実装
クラスの定義
それでは,遺伝的アルゴリズムを実装しましょう. 最初に初期状態を定義します.
START = toGene(route)
インポートしたSearchProblemクラスをオーバライドして,
巡回セールスマン問題を表す TSProblem を定義します.
オーバライドするメソッドは,value,generate_random_state,
crossover,mutate の4種類です.
class TSProblem(SearchProblem):
def value(self, state):
...
def generate_random_state(self):
...
def crossover(self, state1, state2):
...
def mutate(self, state):
...
value(self, state)
個体stateの経路コストを算出します.
巡回セールスマン問題は経路コストを最小化する必要がありますが,
ここでは目的関数を負の値で表し,最大化 を目的とした問題として扱います.
def value(self, state):
route = toRoute(state)
value = -1 * distance(route)
#--------------------
# 途中経過の出力
global max_state
global max_value
if max_value < value:
max_state = state
max_value = value
print(f"max state: {max_state}({max_value:.3f})")
#--------------------
return value
generate_random_state(self)
ランダムに個体geneを生成します.
def generate_random_state(self):
gene = randomGene()
return gene
crossover(self, state1, state2)
個体state1と個体state2を交叉し,新しい個体を生成します.
交叉する位置は乱数で決定します.
def crossover(self, state1, state2):
child = []
index = np.random.randint(0, len(state1))
for i in range(0, index):
child.append(state1[i])
for i in range(index, len(state2)):
child.append(state2[i])
return child
mutate(self, state)
個体stateを突然変異させ,新しい個体を生成します.
突然変異する位置は乱数で決定します.
位置に応じて設定する値の最大値が異なることに注意してください.
例えば,個体の最初の遺伝子は$0,1,\cdots,9$の10通りから選択しますが,
5番目の遺伝子は$0,1,\cdots,4$の5通りから選択します.
def mutate(self, state):
child = list(copy.deepcopy(state))
index = np.random.randint(0, len(child))
max = len(child) - index
child[index] = np.random.randint(0, max)
return child
解の探索
遺伝的アルゴリズムgeneticを用いて解を探索します
ここで,population_sizeは1世代の個体の数,mutation_chanceは突然変異の確率,iterations_limitは世代交代の数です.
経路コストは徐々に減少し,最終的に約$302$になりました.
max_state = START
max_value = -1000
problem = TSProblem(initial_state=START)
result = genetic(problem, population_size=300, mutation_chance=0.4, iterations_limit=100)
max state: [2, 7, 1, 0, 5, 4, 1, 0, 0, 0](-565.698)
max state: [6, 1, 6, 6, 5, 3, 0, 1, 0, 0](-540.774)
max state: [2, 1, 3, 1, 2, 4, 0, 2, 1, 0](-486.344)
max state: [2, 2, 0, 4, 5, 1, 3, 0, 1, 0](-478.315)
max state: [5, 7, 2, 3, 5, 0, 3, 1, 1, 0](-445.342)
max state: [5, 6, 6, 0, 1, 0, 2, 0, 1, 0](-405.025)
max state: [7, 7, 2, 5, 1, 4, 1, 2, 1, 0](-384.451)
max state: [3, 8, 0, 5, 1, 4, 0, 2, 1, 0](-381.537)
max state: [3, 0, 5, 5, 5, 3, 3, 0, 0, 0](-379.105)
max state: [2, 6, 0, 5, 1, 1, 3, 1, 1, 0](-372.361)
max state: [6, 1, 1, 0, 3, 3, 0, 2, 0, 0](-341.490)
max state: [2, 5, 1, 3, 2, 1, 3, 0, 0, 0](-327.178)
max state: [3, 0, 5, 5, 1, 3, 0, 1, 0, 0](-320.839)
max state: [5, 5, 1, 1, 4, 3, 0, 2, 0, 0](-309.094)
max state: [3, 0, 5, 5, 1, 0, 2, 1, 0, 0](-302.755)
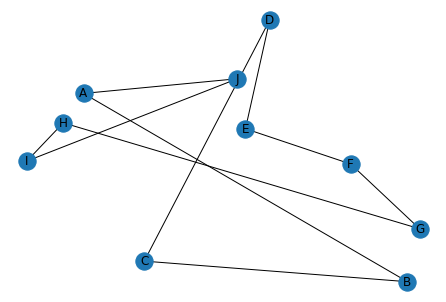
得られた経路を確認すると,経路コストが最短となっていることがわかります.
$$ D \rightarrow A \rightarrow H \rightarrow I \rightarrow C \rightarrow B \rightarrow G \rightarrow F \rightarrow E \rightarrow J \rightarrow D $$
route = toRoute(result.state)
print(route)
# グラフの初期化
graph.clear()
# ノードの設定
graph.add_nodes_from(nodes)
# 経路の設定
graph.add_edges_from(route)
# 描画
nx.draw(graph, pos=pos, with_labels=True)
[('D', 'A'), ('A', 'H'), ('H', 'I'), ('I', 'C'), ('C', 'B'), ('B', 'G'), ('G', 'F'), ('F', 'E'), ('E', 'J'), ('J', 'D')]
課題
ノード数を12まで増やして,最適な巡回路を探索してください. ノードの座標は自由に設定して構いません.
Google Colaboratoryで作成した AI-11.ipynb を保存し, ノートブック(.ipynb) をダウンロードして提出しなさい. 提出の前に必ず下記の設定を行うこと.
- ノートブックの設定で「セルの出力を除外する」のチェックを外す
- ノートブックの変更内容を保存して固定