標準正規分布を用いた検定

t検定とは

検定とは「標本から推定された母数が，確率的に正しいかどうか」を判断することを意味します． 検定は，統計的仮説検定とも呼ばれ，推測統計でも利用頻度の高い重要なテクニックです． 検定を行うための手順は下記のようになります．

1．母数に関する帰無仮説と対立仮説を立てる．
2. 検定統計量を選択する．
3. 信頼区間（棄却域）を決める．
4. 標本から検定統計量を計算する．
5. 検定統計量が棄却域に含まれれば，帰無仮説を棄却して，対立仮説を採用する．棄却域に含まれなければ，帰無仮説を採択する．

難しい単語がたくさん出てきましたが，これは追々説明していきます． ここでは，母集団が正規分布であり，母平均，母分散が既知であるときに適用可能な標準正規分布を用いた検定を考えます． この，標準正規分布を用いた検定 は Z検定 とも呼ばれます．

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します． 次に，[ファイル]-[保存]をクリックして，スクリプトを保存します． このとき，ファイル名はchapter9としてください． また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

検定の目的

まずは下記の具体例を考えていきましょう．

母集団は「文化情報学部の学生$X$」， 標本は「向研究室に所属する学生$x$」と考えることができます． また，「標本平均の分布」を$m$とします． いずれも正規分布に従うと仮定すると，母集団の分布と，標本平均の分布は下記のようになります．

$X \sim N(60,100)$

$m \sim N(60,100/5) = N(60,20)$

ここで，標本の平均を求めてみましょう．

x <- c(63,75,72,67,71)
> mean(x)
[1] 69.6

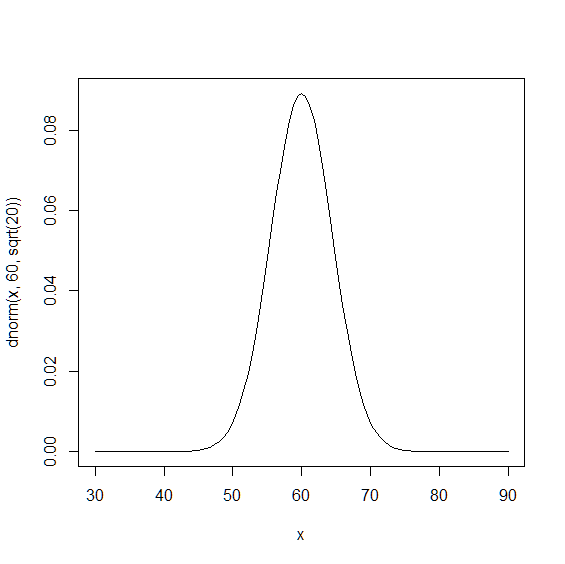
標本平均は69.6点とかなり高得点です． これは，どのくらい珍しいことなのでしょうか． 標本平均の分布のグラフで確認してみましょう．

> curve(dnorm(x,60,sqrt(20)),from=30,to=90)

グラフを確認すると，標本平均が69.6点以上になる確率は，非常に低いことが分かります． pnorm関数を利用して，標本平均が69.6点以上になる確率を計算してみましょう．

> 1-pnorm(69.6,60,sqrt(20))
[1] 0.01591156

よって，母集団からランダムサンプリングで抽出した標本の 平均が69.6点以上になる確率は 約1.6% という結果になりました． これは，「向研究室の学生は母集団とは異なる傾向を持っている」ということを意味します． ようするに凄く優秀な学生が向研究室に集まっているということです（本当にこうなるといいなぁ）．

上記が検定の基本的な考え方です． ここでは，検定に平均60，分散20の正規分布を利用しましたが， 平均0，分散1の標準正規分布を用いるのが Z検定 です．

Z検定

上記の問題を Z検定 で考えていきましょう． まずは，帰無仮説 と 対立仮説 を立てます．

• 帰無仮説：標本（向研究室に所属する学生）の母平均$\hat{\mu}$は60である
• 対立仮説：標本（向研究室に所属する学生）の母平均$\hat{\mu}$は60ではない

対立仮説が証明したい仮説であり，帰無仮説は本来証明したいことと逆の仮説になります． ここで，帰無仮説を正しいとすると，ありえない事象が起こっているとすれば， 帰無仮説は棄却され，対立仮説が採択されることになります．

次に，検定統計量 を選択しますが， ここではZ検定の検定統計量であるZスコアを利用します． Zスコアに関しては，後程，詳しく説明します．

次に，信頼度(棄却域) を定めます． これは，どの程度低い確率で事象が起こっていれば，帰無仮説を棄却するかを示す値です． 一般的には，「95%信頼度（5%棄却域）」，「99%信頼度（1%棄却域）」が用いられます． ここでは，「95%信頼度（5%棄却域）」を用いることにしましょう．

それでは，検定統計量であるZスコアを計算してみましょう． Zスコアは下記の式で求めます． この式は対象の分布を標準化しているにすぎません． 標準化とは平均を0，分散（標準偏差）を1にすることを意味します．

$Z = \frac{\mu - \hat{\mu}}{\sigma}$

• 標本平均$\mu=69.6$
• 標本平均の標準偏差$\sigma=\sqrt{20}$
• 母集団の平均$\hat{\mu}=60$

このとき，標本平均の標準偏差$\sigma$は 下記の式で求められることに注意してください．

$\sigma = \sqrt{ \hat{\sigma}^2 / n }$

• 母集団の標準偏差$\hat{\sigma}=10$
• 標本のサンプル数$n=5$

上記の式を基にZスコアを計算します．

> z <- (69.6 - 60)/ sqrt(20)
> z
[1] 2.146625

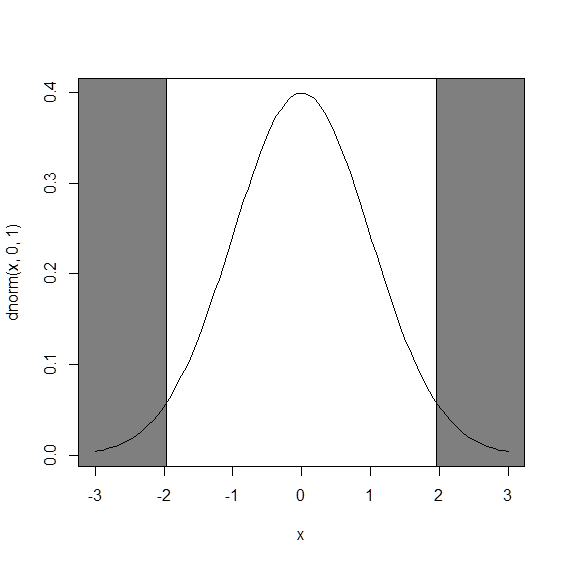
Zスコアは2.14という結果になりました． 標準正規分布を利用して，このZスコアが棄却域に含まれるかを確認しましょう． ここでは，5%棄却域を採用するため，下側確率 が0.025， 上側確率 が 0.975となるZスコアを探します． Zスコア（標準正規分布のパーセント点）を求めるにはqnorm関数を利用します．

> qnorm(0.025,0,1)
[1] -1.959964
> qnorm(0.975,0,1)
[1] 1.959964

上記より，z<-1.96，また，z>1.96 となる確率は5%ということが分かります． これは，下図の左端と右端のグレーの範囲を表しています．

今回の標本のZスコアは2.14だったため，棄却域に含まれ，その確率は5%以下であるということが分かります． よって，帰無仮説（向研究室に所属する学生の母平均は60である）は棄却され， 対立仮説（向研究室に所属する学生の母平均は60ではない）が採択されます． 結果として，先程と同様に，「向研究室の学生は母集団とは異なる傾向を持っている（母集団からランダムサンプリングした標本ではない）」という結論が導かれます． また，このときの母平均$\mu$の95％信頼度の信頼区間は，下記のように求めることができます．

$-1.96 < \frac{69.6 - \mu}{\sqrt{20}} < 1.96 = 60.83 < \mu < 78.36$

これは，「真の母集団から標本を抽出すると，95%の確率で信頼区間（今回は63.81～75.38）に，真の母平均 が含まれる」ということを意味しています． 帰無仮説が棄却されたことから，標本は$\hat{\mu} \neq 60$の真の母集団から抽出されたはずです． つまり，「この真の母集団の平均（母平均）が，この信頼区間にあるだろう」という意味です． よく分かりませんよね． 詳しくは滋賀大学の中川雅央先生の解説を確認しましょう．

課題

向研究室の学生の得点が{65,55,52,45,51}だったときのZスコアを求めなさい． また，検定を用いて，「95%信頼度（5%棄却域）」のときに， 「帰無仮説：標本の母平均$\hat{\mu}$は60である」は棄却されるか調べ，そのときの母平均の信頼区間も求めなさい． ソースはchapter9.Rに記述して提出すること．