正規分布
正規分布
正規分布 は,ガウス分布 とも呼ばれ,平均値に近い値の頻度が高く, 平均値から離れるほど頻度が低くなるという特徴を持った確率分布のことです. 例えば,「身長」や「体重」などの分布が正規分布に従うことが知られており, その他にも様々な社会現象や自然現象に当てはまると考えられています. また,分布が数学的に扱いやすい性質を持っていることから, 統計分析によく用いられ,最も重要な 確率分布 と言っても間違いありません. 今回は,サンプルデータを基に正規分布のグラフを描く事から始め,正規分布を利用して特定の区間の生起確率を求める方法を学びます.
スクリプトの作成
コードを入力し保存するためのスクリプトを作成しましょう. [ファイル]-[新しいスクリプト]をクリックし,Rエディタを表示します. 次に,[ファイル]-[保存]をクリックして,スクリプトを保存します. このとき,ファイル名はchapter7としてください. また,ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます.
正規分布のグラフ
気象庁が公開している 愛知県名古屋市の9月の最高気温のデータを対象に考えていきます. このデータは,1891年から2016年までの,愛知県名古屋市の9月の最高気温を表しています.
年,最高気温
1891,28.7
1892,28.1
1893,28.6
1894,28.4
1895,28.3
1896,27.7
1897,27.3
1898,28
1899,25.4
1900,28.9
...,...
2016,29.3
ファイルをダウンロードしたら,read.csv 関数を利用して, 変数tempにデータフレームとして読み込んでおきましょう(作業ディレクトリはデスクトップに変更).
temp <- read.csv("temperature.csv")
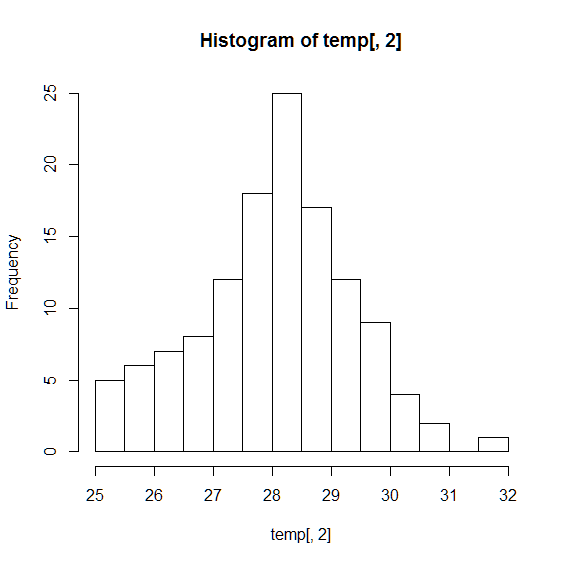
次に,hist関数を利用して,最高気温のヒストグラムを表示しましょう. 範囲は25から32までとし,区間は0.5とします. seq関数は,規則性のある数列ベクトルを生成する関数であり, ここでは,25から32まで,0.5ずつ増やした数列({25.0,25.5,26.0,26.5,…,32})を生成します.
hist(temp[,2],breaks=seq(25,32,0.5))
グラフを確認すると, 区間28-8.5 が最頻値となっていることが分かります. また,この区間から離れるにつれて緩やかに頻度が減り, 全体としては左右対称な 釣鐘型 と呼ばれる分布をしています. しかし,このグラフは,縦軸が頻度を表すヒストグラムであり,確率分布ではありません. そこで,hist 関数の引数にfreq=FALSE を設定し,縦軸を 確率密度 に変更します.
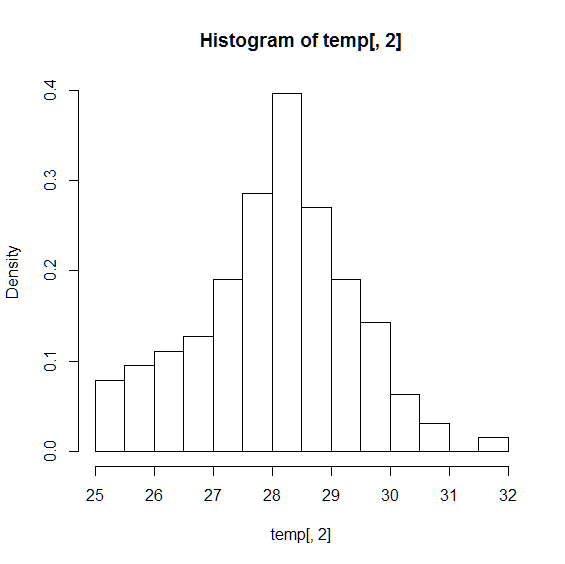
hist(temp[,2],breaks=seq(25,32,0.5),freq=FALSE)
ここでのポイントは,縦軸は 確率 ではなく 確率密度 を表しているということです. 前回の2項分布では,「コインの表が出る回数」は非連続の値をとることから,離散分布であり,縦軸が表す値は 確率 になります. 一方,「気温」は連続的な値をとることから, 連続分布 であり,縦軸が表す値は 確率密度 になります. このため,連続分布において 確率 は,グラフの面積で表されます(面積の和が1になる). 例えば,区間28-28.5の確率は,下記のように求めます. ここで,0.5は区間(幅)を表し,d$density[7]は区間28-28.5の確率密度(高さ)を表しています. これを掛け合わせることで確率(面積)になるということです.
> d <- hist(temp[,2],breaks=seq(25,32,0.5),freq=FALSE)
> 0.5 * d$density[7]
[1] 0.1984127
正規分布 は上記のような釣鐘型の連続グラフを近似する場合に利用されます.
正規分布の公式
それでは正規分布の公式を利用して,先程の最高気温のヒストグラムを近似してみます. 正規分布の 確率密度 は下記の式で定義されます.
2項分布に比べると,とても難しい式にみえます. しかし,正規分布は対象のデータの平均と 標準偏差が分かれば求めることができます. そこで,下記のように,mean 関数,sd 関数で平均と標準偏差を求めます.
mu <- mean(temp[,2])
sigma <- sd(temp[,2])
次に,この平均と 標準偏差に従う正規分布の確率密度を求めます. R言語では,dnorm関数を用いることで,正規分布の確率密度の計算が可能です. 例えば,x=28の確率密度を求めるには,下記のように入力します.
> dnorm(28,mu,sigma)
[1] 0.3013075
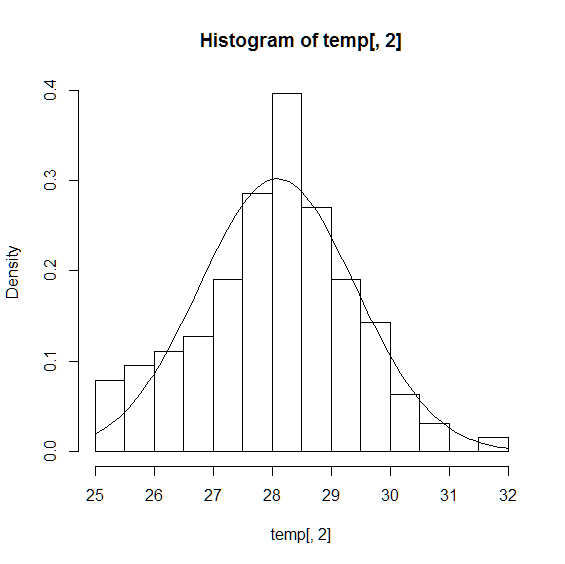
それでは,先程描いたヒストグラムに,正規分布の確率密度のグラフを重ねてみましょう. curve関数を利用することで,特定の関数のグラフを描くことができます. また引数のadd=TRUEはグラフを重ねて描くことを意味しています.
> hist(temp[,2],breaks=seq(25,32,0.5), freq=FALSE)
> curve(dnorm(x,mu,sigma),add=TRUE)
ヒストグラムと正規分布の形状がとても良く似ており,正規分布で近似できそうだということが分かります. では,先程と同様に,28.0-28.5の区間の確率,つまり 面積 を求めてみます. 正規分布は,ヒストグラムの区間を0に近づけた形状と考えられるため, 面積を求めるには対象区間の 積分 を求める必要があります. 積分された面積の値は pnorm関数で求めることができます. このような関数を 累積分布関数 といいます. 例えば,x=28以下となる確率は,下記のように入力します.
> pnorm(28,mu,sigma)
[1] 0.4726962
それでは,28.0-28.5の区間の確率を求めましょう. この確率は「28.5以下となる確率」から「28以下となる確率」を引くことで求められます.
> pnorm(28.5,mu,sigma) - pnorm(28,mu,sigma)
[1] 0.1490331
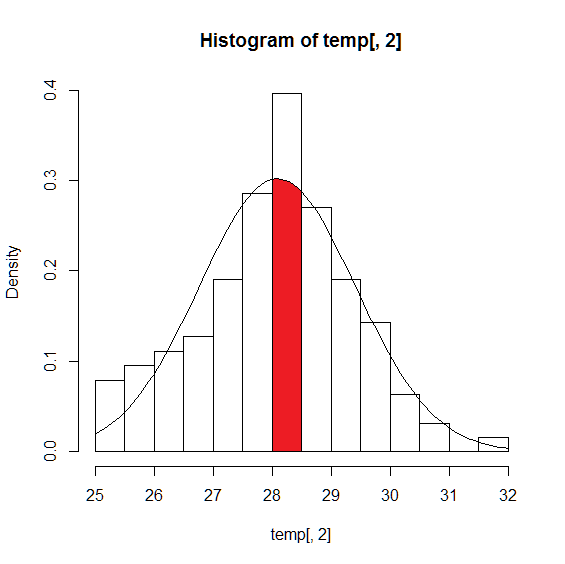
この結果,最高気温が28.0~28.5になる確率は, 正規分布に従うと**14.9%になるということが分かります. 下図では,赤色に塗り潰された箇所の面積が,全体に対して14.9%**ということになります.
課題
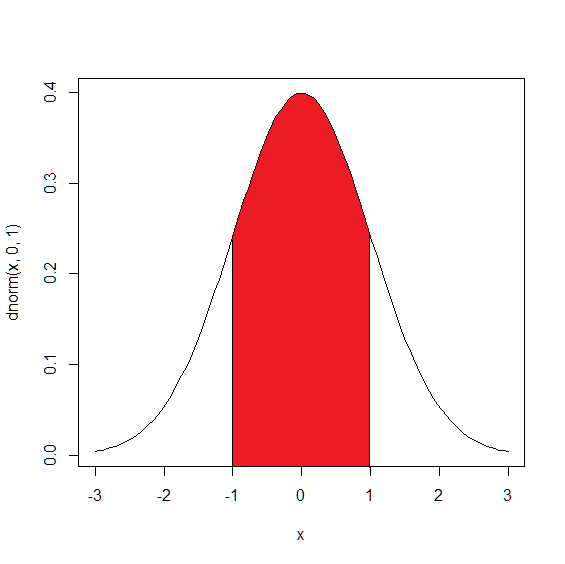
平均,標準偏差の 正規分布を 標準正規分布 と呼びます. xの範囲が-3から3までの,標準正規分布のグラフを描いてください(curve 関数で from=-3,to=3 を引数に設定). また,からまでの区間の確率をもとめてください. ソースはchapter7.Rに記述し,グラフ(標準正規分布)の画像ファイル,chapter7.R を提出すること.