2項分布
2項分布
2項分布とは,結果が2通り(例,成功・失敗)となる試行を複数回行ったときの確率分布です. 例えば,「コインを投げる」という試行の結果は,表,または,裏のどちらかになります. 他にも,「サイコロを投げる」という試行の結果は,偶数,または,奇数のどちらかになります. このような試行はベルヌーイ試行と呼ばれ,ベルヌーイ試行を複数回行ったときの結果が2項分布に従います. 今回は,サンプルデータを基に2項分布のグラフを描く事から始め,2項分布を利用して生起確率を求める方法を学びます.
スクリプトの作成
コードを入力し保存するためのスクリプトを作成しましょう. [ファイル]-[新しいスクリプト]をクリックし,Rエディタを表示します. 次に,[ファイル]-[保存]をクリックして,スクリプトを保存します. このとき,ファイル名はchapter6としてください. また,ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます. このとき,グラフ描画に必要なggplot2も読み込んでおきましょう.
library(ggplot2)
2項分布のグラフ
まずは「コインを投げる」という試行に注目しましょう. 試行の結果は,表 と 裏 の2通りですが,ここでは便宜的に,1 と 0 で表現します. このとき,1 が出る確率は50%と仮定します.当然,0 が出る確率も50%です. この試行を10回繰り返して行ない,1 が出た数をカウントします.
乱数を生成するsample関数を用いて,上記の試行の結果を生成してみましょう. 引数には,「取り得る値のベクトル(ここでは,0または1)」,「乱数の個数(ここでは10回)」,「重複の許可」を設定します. 結果は下記のようになりました(乱数なので結果は毎回変わる). 10回投げて,表が5回,裏も5回という結果です.
> sample(0:1,10,replace=TRUE)
[1] 0 1 1 1 0 0 1 0 0 1
さらに,この試行(「コインを10回投げる」)を1000回繰り返し,配列に変換して変数coinに代入しましょう.
coin <- matrix(sample(0:1,10000,replace=TRUE),1000,10)
coinは1000行,10列の配列になります. これが,試行を1000回繰り返した結果を表しています.
> coin[1:10,]
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 1 0 1 0 1 0 1 1 1
[2,] 0 0 1 1 1 0 0 1 1 0
[3,] 1 0 0 0 1 1 0 1 1 1
[4,] 0 0 1 0 0 1 1 1 0 0
[5,] 0 1 0 1 0 1 1 0 0 0
[6,] 0 1 1 0 0 0 1 1 1 1
[7,] 0 0 1 1 1 1 1 0 1 1
[8,] 1 1 0 0 1 0 1 0 1 1
[9,] 1 0 0 0 0 1 1 0 1 0
[10,] 0 0 0 0 1 1 1 1 0 1
次に,各試行の表の出た回数をカウントし,ベクトルcountに代入します. 各行の総和を求めるにはrowSums関数を用います.
count <- as.vector(rowSums(coin))
結果は下記のようになりました. このベクトルは,「コインを10回投げる」を1000回繰り返したときの「表が出た回数」を表しています.
> count[1:100]
[1] 6 5 6 4 4 6 7 6 4 5 4 5 6 5 5 6 6 3 6 7 4 5 7 2 5 6 5 7 6 4 5 4 5 7 6 4
[37] 4 5 6 4 5 5 4 4 5 5 8 4 4 5 4 5 7 7 6 4 7 5 4 4 4 5 5 6 6 4 5 5 9 9 3 6
[73] 5 9 5 4 2 6 4 5 3 7 5 5 7 6 6 6 5 4 8 6 7 3 2 6 6 6 5 6
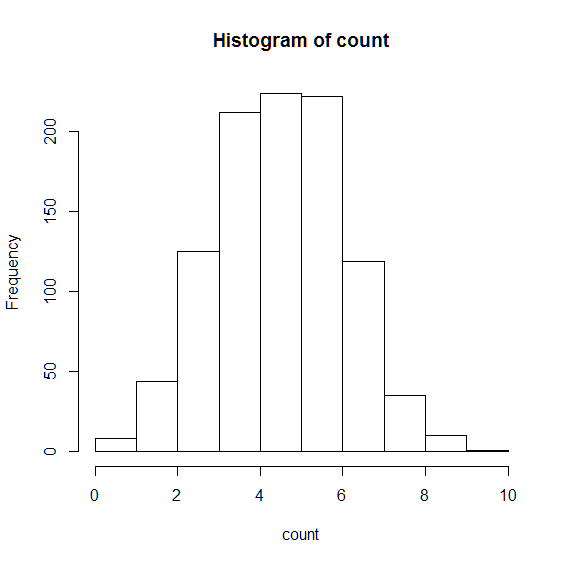
では,hist関数を利用してヒストグラムを作成しましょう. 引数のbreaksは描画するX軸の範囲をベクトルで指定しています.
hist(count,breaks=c(0:10))
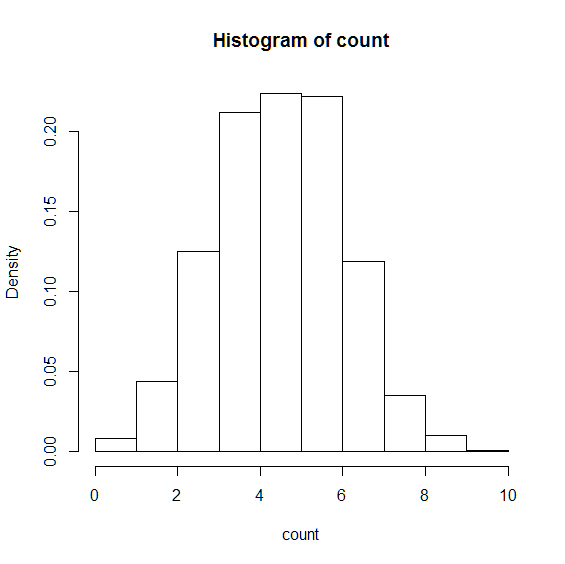
「表が5回出る」が最頻値となっており,0回や10回に近づく程,その発生頻度は下がっていくことが分かります. このグラフは,縦軸が頻度を表すヒストグラムであり,確率分布ではありません. そこで,hist 関数の引数に freq=FALSE を設定し,縦軸が確率を表す確率分布に変更します.
hist(count,breaks=c(0:10),freq=FALSE)
この確率分布が 2項分布 です. これは1000回の繰り返しの結果ですが,試行回数が増えるほどに,確率分布は理想の形状に近付いていきます.
2項分布の公式
理想的な2項分布はどのような形状でしょうか. 2項分布の公式を基に考えてみましょう. 1回の生起確率が p のベルヌーイ試行を,n 回行って, k回起こる確率は下記の式で与えられます. ここで, は「 n 個の中から k 個を選ぶ組み合わせの数を表しています.
先程のコインの例で考えると,生起確率p=0.5,試行回数 n=10 であり, 例えば, 表が k=5 回だけ出る確率は下記の式で計算されます.
この計算はR言語では,dbinom関数を用います. 引数には,k,n,pの順番で設定します.
> dbinom(5,10,0.5)
[1] 0.2460938
結果は0.246となり,上記の結果と一致することが分かります. dbinom関数は,k をベクトルとすることで,一度に複数の確率を計算することができます. ここでは,dbinom関数で得た確率のベクトルを,下記のようにデータフレームに変換します.
dist <- dbinom(c(0:10),10,0.5)
binom <- data.frame(k=c(0:10),p=dist)
コンソールでデータフレームbinomを確認します.
> binom
k p
1 0 0.0009765625
2 1 0.0097656250
3 2 0.0439453125
4 3 0.1171875000
5 4 0.2050781250
6 5 0.2460937500
7 6 0.2050781250
8 7 0.1171875000
9 8 0.0439453125
10 9 0.0097656250
11 10 0.0009765625
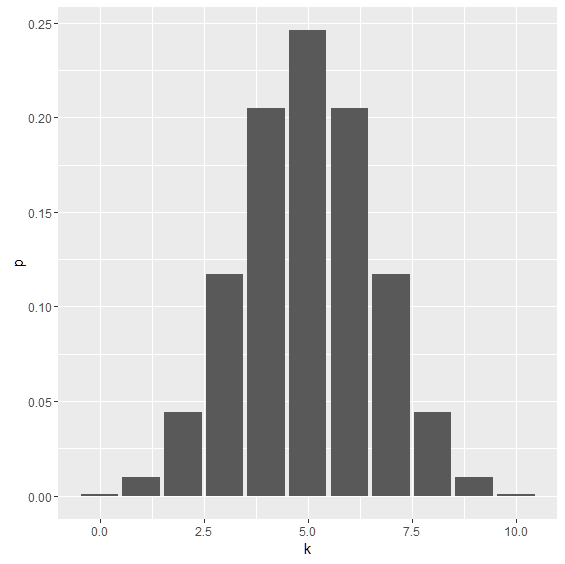
このデータフレームを,ggplot 関数を利用して,グラフにしましょう.
> ggplot(binom,aes(x=k,y=p))+geom_bar(stat="identity")
これが理想的な2項分布の形状です. 1000回の繰り返しのグラフと同様に,「表が5回出る」の確率が最も高く,0回や10回の確率は非常に低いことが分かります.
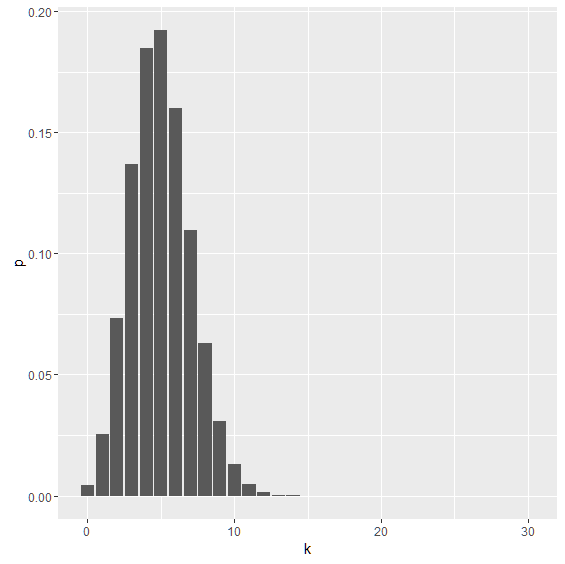
課題
「サイコロを30回投げる」という試行を考え,「1の目」が出る事象の2項分布のグラフを描きなさい. ただし,サイコロに細工はなく,1/6の確率で「1の目」が出るとする. ソースはchapter6.Rに記述し,グラフ(2項分布)の画像ファイル,chapter6.R を提出すること.