相関係数
相関分析
相関分析とは,2種類のデータの関係性を測るための方法を指します. 例えば,夏の熱い日には,アイスクリームがよく売れるとします. このとき,温度と,アイスクリームの売上には相関があると言えます. 今回は,このようなデータの相関を調べるに共分散と相関係数を学びましょう. 対象のデータは,前回と同じ成績のデータ(CSV形式)を使用します. このデータは15人の生徒の国語,算数,理科,英語,社会の得点で構成されています.
ファイルをダウンロードしたら,read.csv関数を利用して, 変数scoreにデータフレームとして読み込んでおきましょう(作業ディレクトリはデスクトップに変更).
score <- read.csv("score.csv")
変数scoreの出力は下記のようになります.
> score
氏名 国語 算数 理科 英語 社会
1 青木 達也 60 68 72 39 71
2 石井 健二 65 78 82 37 75
3 北村 真子 84 59 85 87 84
4 河野 尚子 50 65 65 39 78
5 高木 健 72 74 83 30 83
6 西川 知里 50 29 67 62 72
7 福島 萌子 84 40 65 86 66
8 古川 翔太 78 71 82 34 88
9 山内 香菜 77 33 65 73 88
10 渡辺 太郎 76 53 75 60 71
11 浅野 渉 68 46 77 66 86
12 星野 弘 61 27 74 70 67
13 中谷 章 86 57 72 73 65
14 小泉 美沙 68 48 73 51 68
15 木下 萌子 78 90 100 53 79
スクリプトの作成
コードを入力し保存するためのスクリプトを作成しましょう. [ファイル]-[新しいスクリプト]をクリックし,Rエディタを表示します. 次に,[ファイル]-[保存]をクリックして,スクリプトを保存します. このとき,ファイル名はchapter5としてください. また,ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます.
散布図
データの相関を視覚的に確認するには散布図を利用するのが最も簡単です. X軸に算数,Y軸に理科として,散布図を描いてみましょう. まずは,グラフ描画のためのライブラリであるggplot2を読み込みます.
library(ggplot2)
次に,プロンプトでqplot関数を利用して散布図を描きます.
> qplot(算数,理科,data=score)
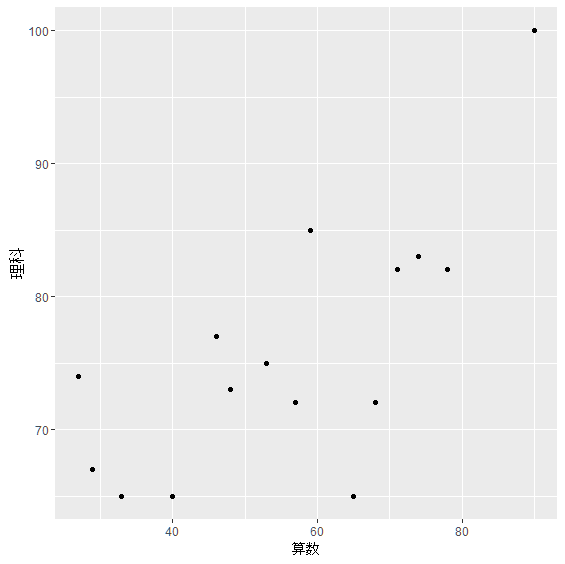
すると下記のような散布図がプロットされます. 算数と理科にはどのような関係があるでしょうか. どちらかといえば,数学が高得点であるほど,理科も高得点となっており, 右上がりの傾向がありそうではないでしょうか. このような関係を正の相関といいます.
次に,X軸に算数,Y軸に英語として,散布図を描いてみましょう.
プロンプトでqplot関数を利用して散布図を描きます.
> qplot(算数,英語,data=score)
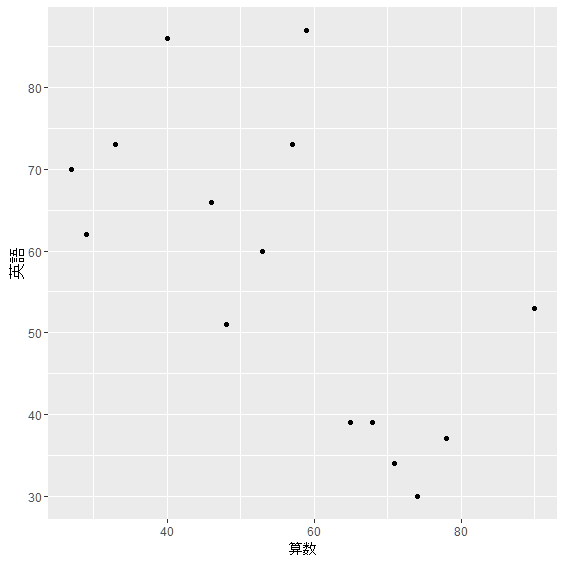
こんどは,数学が高得点であるほど,英語は低い得点となっており, 右下がりの傾向がありそうではないでしょうか. このような関係を負の相関といいます.
最後に,X軸に算数,Y軸に国語として,散布図を描いてみましょう.
プロンプトでqplot関数を利用して散布図を描きます.
> qplot(算数,国語,data=score)
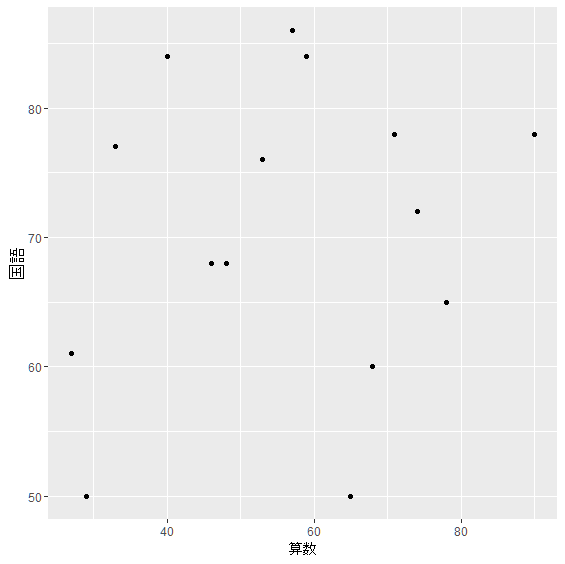
先程と比べると,特に傾向が見当たりませんね. このような関係を無相関といいます.
共分散
次に,データの相関を定量的に計算して求めてみましょう. まずは共分散という指標を用います. 共分散は「偏差の積の平均」を表します. 例えば,算数と理科の共分散は下記の式で求めます.
まずは,この式に忠実に,下記のようにスクリプトを記述して計算してみましょう.
#算数の偏差
hensa_sansu = score[,3] - mean(score[,3])
#理科の偏差
hensa_rika = score[,4] - mean(score[,4])
#共分散
kyo_bunsan <- sum(hensa_sansu * hensa_rika) / length(score[,3])
プロンプトで共分散の値を確認してみましょう.
> source("chapter5.R")
> kyo_bunsan
[1] 119.1067
共分散の値は約119.1になりました. R言語では,covという関数で共分散を求めることができます. 今度は,cov関数で共分散を計算してみましょう.
> cov(score[,3],score[,4])
[1] 127.6143
先程とは異なる結果になりました. これは,前回と同じように,標本分散と不偏分散の違いが原因です 今回も下記のように分母をn-1に変更します.
#共分散
kyo_bunsan <- sum(hensa_sansu * hensa_rika) / (length(score[,3]) - 1)
プロンプトで共分散の値を確認してみましょう.
> kyo_bunsan
[1] 127.6143
今度は共分散が約127.6となり,cov関数で求めた値と一致しました. 同様に,算数と英語,算数と国語の共分散を計算してみましょう.
> cov(score[,3],score[,5])
[1] -219.5238
> cov(score[,3],score[,2])
[1] 36.49524
まとめると,共分散は下記のようになります.
| 科目1 | 科目2 | 共分散 |
|---|---|---|
| 算数 | 理科 | 127.6143 |
| 算数 | 英語 | -219.5238 |
| 算数 | 国語 | 36.49524 |
散布図で確認したように,算数と理科は大きな正の値,算数と英語は大きな負の値 ,算数と国語は小さな正の値になっていることが確認できます. このように,共分散を求めることで,2種類のデータの相関を定量的に表すことができます. しかし,共分散は,対象となるデータのスケール(縮尺) に依存するという問題があります. 例えば,100点満点と200点満点の試験では,相関を比較することができません. そこで,次節で説明する相関係数が登場します.
相関係数
スケールに依存しない相関を計算するには,まずは相関係数を用います. 相関係数は,先に求めた共分散を,2変数の標準偏差の積で割って求めます. 例えば,算数と理科の標準偏差は下記の式で求めます.
下記のようにスクリプトを記述して計算してみましょう.
#相関係数
soukan <- kyo_bunsan / (sd(score[,3]) * sd(score[,4]))
プロンプトで相関係数の値を確認してみましょう.
> soukan
[1] 0.7128868
相関係数は約0.71になります. R言語では,corという関数で相関係数を求めることができます. 今度は,cor関数で共分散を計算してみましょう.
> cor(score[,3],score[,4])
[1] 0.7128868
先程の値と一致しました. 同様に,算数と英語,算数と国語の共分散を計算してみましょう.
> cor(score[,3],score[,5])
[1] -0.6243508
> cor(score[,3],score[,2])
[1] 0.1676487
まとめると,相関係数は下記のようになります.
| 科目1 | 科目2 | 相関係数 |
|---|---|---|
| 算数 | 理科 | 0.7128868 |
| 算数 | 英語 | -0.6243508 |
| 算数 | 国語 | 0.1676487 |
このように,相関係数の値は0から1の範囲をとります. 算数と理科は1に近く強い正の相関,算数と英語は-1に近く負の相関, 算数と国語は0に近く無相関ということが読み取れます.
課題
2016年度の中日ドラゴンズの打撃成績のデータ(CSV形式)から, 盗塁と強い相関(相関係数が0.7以上)を示す項目を探してください (出典:プロ野球ヌルデータ置き場). ソースはchapter5.Rに記述し,chapter5.R を提出すること.