因子分析

因子分析とは

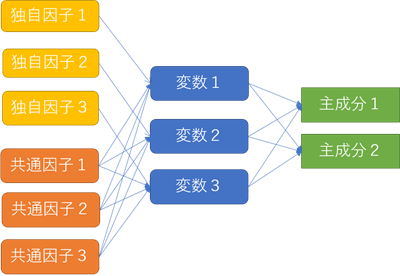
因子分析は，主成分分析と同じ多変量解析の手法の一つです．主成分分析は観測された変数を合成することが目的であるのに対し，因子分析は観測された変数そのものが 潜在変数（因子） の合成であるとみなします．下図は，主成分分析と因子分析の違いを表しています．主成分は，全ての変数を合成することで求められます．一方，因子は，独自因子 と 共通因子 に分かれており， 独自因子 は特定の変数に影響するのに対し，共通因子 は複数の変数に影響を与えます．

主成分分析は，次元を圧縮することで，データを可視化することに向いていますが，変数間の関係を分析することは苦手です．一方，因子分析は得られた因子は変数間の関係を表しており，データの分析に適しています．しかし，因子分析は，主成分分析より数学的に難解であり，その仕組を完全に理解することは容易ではありません．因子分析だけで本が一冊書けてしまう程であり，統計だけではなく，行列，ベクトルなどの知識が不可欠です．今回も，理解より 使える ことを重要視して，因子分析を学びましょう．対象のデータとして，５教科の 成績のデータ（CSV形式） を使用するので，事前にダウンロードしておきましょう．

ファイルをダウンロードしたら，read.csv 関数を利用して，変数scoreにデータフレームとして読み込んでおきましょう．

score <- read.csv("score.csv")

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタ を表示します．次に，[ファイル]-[保存]をクリックして，スクリプトを保存します．このとき，ファイル名はchapter14としてください．また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

主成分得点と因子

ここで，もう一度，主成分分析と因子分析の違いを整理しておきましょう．主成分得点は下記の式で表すことができます．ここで， $x_1，x_2$ は，国語や算数の得点など変数を表しており，

$w_1，w_2$ は，

それら変数の重みであると共に，主成分を表すベクトルでした．

$f(X) = w_1 \times x_1 + w_2 \times x_2$

一方，因子分析は下記の式で表すことができます．ここで， $f_1(X)，f_2(X)$ は因子得点と呼ばれます．この因子得点は，共通因子の影響を得点に換算した推定値であり，個体ごとに得点が決まります．また， $w_1，w_2$ は，因子得点の重みであり，因子負荷量 と呼びます．主成分を表すベクトルとは異なり， $||w|| = 1$ という条件は満たしません（ベクトルの長さにも意味があります）．注意すべきは，独自因子の $e$ であり，これが主成分分析との大きな違いを生みます（ $e=0$ とすると主成分分析と同じアプローチになる）．

$x = w_1 \times f_1(X) + w_2 \times f_2(X) + e$

データの標準化

因子分析を始める前にデータを標準化します．標準化とは，対象となるデータの平均 $\mu$ を0，分散 $\sigma^2$ を1にすることを意味します．

$x^{,} = \frac{x - \mu}{\sigma}$

R言語では，scale関数で簡単に標準化が可能です．標準化すると下記のように得点が変換されます．

> data <- scale(as.matrix(score[2:6]))
> data
		国語    算数   理科   英語   社会
 [1,] -0.904  0.6452 -0.399 -0.981 -0.616
 [2,] -0.472  1.1769  0.651 -1.088 -0.130
 [3,]  1.169  0.1666  0.967  1.587  0.965
 [4,] -1.768  0.4856 -1.135 -0.981  0.235
 [5,]  0.132  0.9642  0.756 -1.462  0.843
 [6,] -1.768 -1.4286 -0.925  0.250 -0.494
 [7,]  1.169 -0.8437 -1.135  1.533 -1.224
 [8,]  0.651  0.8047  0.651 -1.248  1.451
 [9,]  0.564 -1.2159 -1.135  0.838  1.451
[10,]  0.478 -0.1524 -0.084  0.143 -0.616
[11,] -0.213 -0.5246  0.126  0.464  1.208
[12,] -0.818 -1.5349 -0.189  0.678 -1.102
[13,]  1.342  0.0603 -0.399  0.838 -1.346
[14,] -0.213 -0.4183 -0.294 -0.339 -0.981
[15,]  0.651  1.8149  2.542 -0.232  0.357
attr(,"scaled:center")
国語 算数 理科 英語 社会 
70.5 55.9 75.8 57.3 76.1 
attr(,"scaled:scale")
 国語  算数  理科  英語  社会 
11.58 18.81  9.52 18.70  8.22

因子数の決定

最初に抽出する 因子数 を決める必要があります．原理的には変数と同じだけ因子の抽出が可能ですが（後述する回転をしない場合），主成分分析のように説明力（分散の大きさ）のある因子のみを抽出します． 因子数 を決めるには対象のデータの 相関行列 の固有値と固有ベクトルを計算します．

相関行列 は，各科目間の相関係数を行列で表現したもので，cor関数で求めることができます．下記が相関行列であり，対角成分の値を境に，対象な行列となっていることが分かります（例，国語と算数の相関係数は0.168）．

> correlation <- cor(data)
> correlation
	  国語   算数   理科   英語   社会
国語 1.000  0.168  0.332  0.448  0.117
算数 0.168  1.000  0.713 -0.624  0.272
理科 0.332  0.713  1.000 -0.244  0.340
英語 0.448 -0.624 -0.244  1.000 -0.210
社会 0.117  0.272  0.340 -0.210  1.000

この相関行列の固有値と固有ベクトルを求めます．固有値と固有ベクトルの意味は割愛しますが，行列を複数のベクトルに分解すると考えてください．詳しく知りたい場合は，kenmatsu4氏の「固有値・固有ベクトルとは何かを可視化してみる」が分かりやすいです．例えば，３行３列のベクトル $A$ の固有値と固有ベクトルを求めると，下記のように３組の固有値と固有ベクトルが抽出されます．このとき， $\lambda_1，\lambda_2，\lambda_3$ が固有値（スカラー値），

$\vec{b}=(b_1,b_2,b_3)，\vec{c}=(c_1,c_2,c_3)，\vec{d}=(d_1,d_2,d_3)$ が固有ベクトルです．

実は，固有ベクトルは，主成分分析における主成分を表すベクトルと一致し，その長さは1となります．一方，固有値は，固有ベクトルに射影されたデータ分散を表しています．主成分分析と同様に，分散が大きいほどデータの特徴を表していると考え，一般に $\lambda \geq 1$ の固有値のみを採用し，その数を抽出する因子数と考えます．

$A = \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix}$

$\lambda_1 \begin{pmatrix} b_1 \\ b_2 \\ b_3 \end{pmatrix} ， \lambda_1 \begin{pmatrix} c_1 \\ c_2 \\ c_3 \end{pmatrix} ， \lambda_1 \begin{pmatrix} d_1 \\ d_2 \\ d_3 \end{pmatrix}$

固有値と固有ベクトルを求めるには，eigen関数を利用します． 5つの固有値が抽出され，1以上となるのは，2.268と，1.468の2つであることが分かります．よって，因子数は２が適切だと考えます．

eigen <- eigen(correlation)
> eigen$value
[1] 2.268 1.468 0.811 0.341 0.112
> eigen$vector
	   [,1]    [,2]    [,3]    [,4]    [,5]
[1,] -0.107 -0.7609 -0.1268  0.5411 -0.3175
[2,] -0.611  0.0304 -0.3094  0.2508  0.6833
[3,] -0.550 -0.2685 -0.1830 -0.7069 -0.3035
[4,]  0.428 -0.5802  0.0649 -0.3776  0.5771
[5,] -0.359 -0.1068  0.9222  0.0448  0.0847

共通因子の推定

因子数を基に共通因子を推定していきましょう．ここで，ポイントとなるのは独自因子 $e$ です．この独自因子の平均を0，分散を $d^2$ と仮定します．また，因子得点の平均を0，分散を1とし，因子間の相関は0と仮定します．相関行列が対称行列であることを利用すると，相関行列は下記のように表すことができます（この計算は非常に難解なので割愛）．ここで， $r$ は独自因子を考慮しないときの相関係数です．

$\begin{pmatrix} 1-d_{1}^{2} & r_{12} & r_{13} \\ r_{21} & 1-d_{2}^{2} & r_{23} \\ r_{31} & r_{32} & 1-d_{3}^{2} \end{pmatrix} = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix} \begin{pmatrix} a_{11} & a_{21} & a_{31}\\ a_{12} & a_{22} & a_{32} \end{pmatrix}$

上記の $a$ が因子負荷量であり，独自因子を考慮した相関行列の固有値の平方根と固有ベクトルを掛けて求めることができます．固有値は分散を表すため，平方根をとれば標準偏差を表すことになります．

$\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix} = \begin{pmatrix} \sqrt{\lambda_1}b_1 & \sqrt{\lambda_2}c_2 \\ \sqrt{\lambda_1}b_2 & \sqrt{\lambda_2}c_2 \\ \sqrt{\lambda_1}b_3 & \sqrt{\lambda_2}c_2 \end{pmatrix}$

このとき， $1-d^2$ は，共通因子で説明可能な分散を表し，共通性と呼ばれます．対照的に， $d^2$ は，独自因子で説明可能な分散を表し，独自性と呼ばれます．独自性 $d^2$ は，削った3つの固有値・固有ベクトルの影響を，まとめて表していると考えることができます．ここで，理想の因子負荷量を導出するために， 1を超えない範囲で，共通性 $1-d^2$ を最大化します．

それでは，factanal関数を利用して，因子負荷量を導出します．引数のfactorsは因子数，rotationは回転方法，scoresは因子得点の計算方法を表します（回転方法と因子得点の計算方法は後述）．

> result <- factanal(data,factors=2,rotation="none",scores="regression")
> print(result,cutoff=0)

Call:
factanal(x = data, factors = 2, scores = "regression", rotation = "none")

Uniquenesses:
 国語  算数  理科  英語  社会 
0.426 0.080 0.350 0.005 0.898 

Loadings:
	 Factor1 Factor2
国語  0.431   0.623 
算数 -0.647   0.709 
理科 -0.267   0.761 
英語  0.997   0.029 
社会 -0.216   0.236 

			   Factor1 Factor2
SS loadings      1.716   1.526
Proportion Var   0.343   0.305
Cumulative Var   0.343   0.648

Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.74 on 1 degree of freedom.
The p-value is 0.39

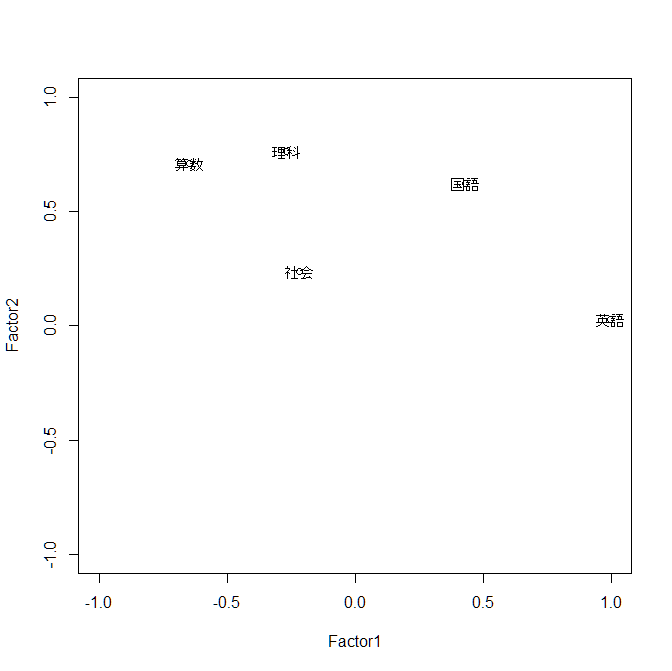
上記の結果から， 因子負荷量（Factor Loadings） を読み取ると， 因子1（Factor1） は，英語と算数の影響が強く， 因子2（Factor2） は，算数と理科の影響が強いことが分かります．また，独自性（Uniquenesses）を読み取ると，算数と英語の値が低く，共通因子で上手く説明できることが分かります．最後に，求めた因子負荷量をグラフで表しておきます．

> plot(result$loadings,xlim=c(-1,1),ylim=c(-1,1))
> text(result$loadings,rownames(result$loadings))

因子の回転

上記で求めた因子負荷量の特徴をより明確にするめに軸の回転を行います．軸の回転には直交回転のバリマックス法，斜向回転のプロマックス法がありますが，ここでは，バリマックス法を採用します．直交回転とは，因子の軸が互いに直交したまま，回転することを意味します．

> result2 <- factanal(data,factors=2,rotation="varimax",scores="regression")
> print(result2,cutoff=0)

Call:
factanal(x = data, factors = 2, scores = "regression", rotation = "varimax")

Uniquenesses:
 国語  算数  理科  英語  社会 
0.426 0.080 0.350 0.005 0.898 

Loadings:
	 Factor1 Factor2
国語  0.233   0.721 
算数  0.956  -0.083 
理科  0.767   0.250 
英語 -0.583   0.809 
社会  0.319  -0.028 

			   Factor1 Factor2
SS loadings      1.996   1.245
Proportion Var   0.399   0.249
Cumulative Var   0.399   0.648

Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.74 on 1 degree of freedom.
The p-value is 0.39

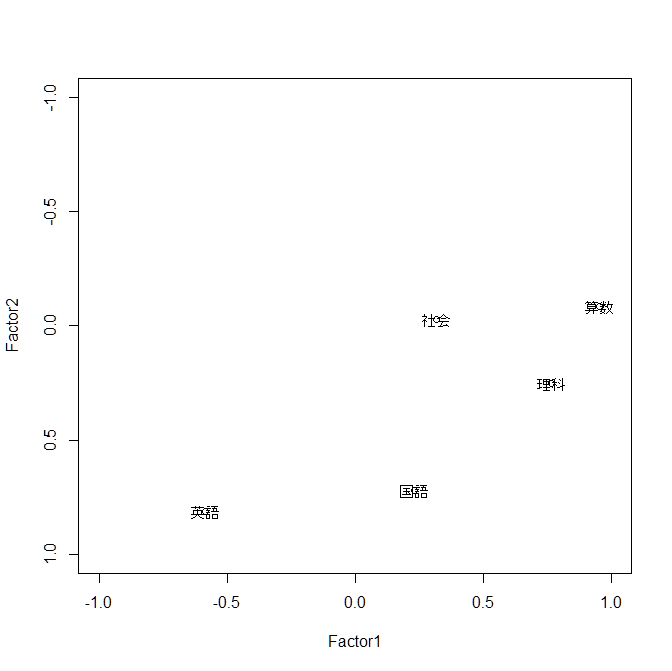
上記の結果から，因子負荷量（Factor Loadings） を読み取ると， 因子1（Factor1） は，算数と理科の影響が強く， 因子2（Factor2） は，国語と英語の影響が強いことが分かります．また，独自性（Uniquenesses）に関しては，回転前と同じ値です．ここで，各因子に意味付けをしておきましょう．因子1は，理系分野の能力を表すことから「理系因子」，一方，因子2は，文系分野の能力を表すことから「文系因子」と考えることができそうです．このとき，社会は独自性が強く，理系因子，文系因子のどちらの影響も弱いことが分かります．最後に，求めた因子負荷量をグラフで表しておきます．先程のグラフと比べると，軸の直交を保ちながら，回転していることが分かります．

> plot(result2$loadings,xlim=c(-1,1),ylim=c(1,-1))
> text(result2$loadings,rownames(result2$loadings))

因子得点

最後に因子得点 $f(X)$ を推定します．因子得点は上記で意味付けをした理系因子と文系因子の得点を表します．因子得点を求めるには回帰法， バートレット法 ， アンダーソン・ルビン法 などがありますが，いずれも推定値であり，正確な値を求めることはできません．ここでは回帰法を採用し，データ，相関行列の逆行列，因子負荷行列を掛けて因子得点を算出します．因子得点は平均0，分散1で標準化されていることに注意してください．

> data %*% solve(correlation) %*% result2$loadings
		  Factor1    Factor2
 [1,]  0.41451018 -0.9142532
 [2,]  1.05474389 -0.5843555
 [3,]  0.22592718  2.1020917
 [4,]  0.09254249 -1.1557858
 [5,]  1.05882559 -1.0257496
 [6,] -1.43614656 -0.7290921
 [7,] -0.90884192  1.2319116
 [8,]  0.96771712 -0.8236710
 [9,] -1.09443243  0.2522387
[10,] -0.10346988  0.1067041
[11,] -0.41795516  0.2682362
[12,] -1.34922263 -0.1318741
[13,] -0.01703708  1.0186440
[14,] -0.35255045 -0.6608092
[15,]  1.86538968  1.0457642

factanal関数と同時に求められた因子得点（result2$scores）と比較してみましょう．値が一致していることが確認できます．

> result2$scores
	  Factor1 Factor2
 [1,]  0.4145  -0.914
 [2,]  1.0547  -0.584
 [3,]  0.2259   2.102
 [4,]  0.0925  -1.156
 [5,]  1.0588  -1.026
 [6,] -1.4361  -0.729
 [7,] -0.9088   1.232
 [8,]  0.9677  -0.824
 [9,] -1.0944   0.252
[10,] -0.1035   0.107
[11,] -0.4180   0.268
[12,] -1.3492  -0.132
[13,] -0.0170   1.019
[14,] -0.3526  -0.661
[15,]  1.8654   1.046

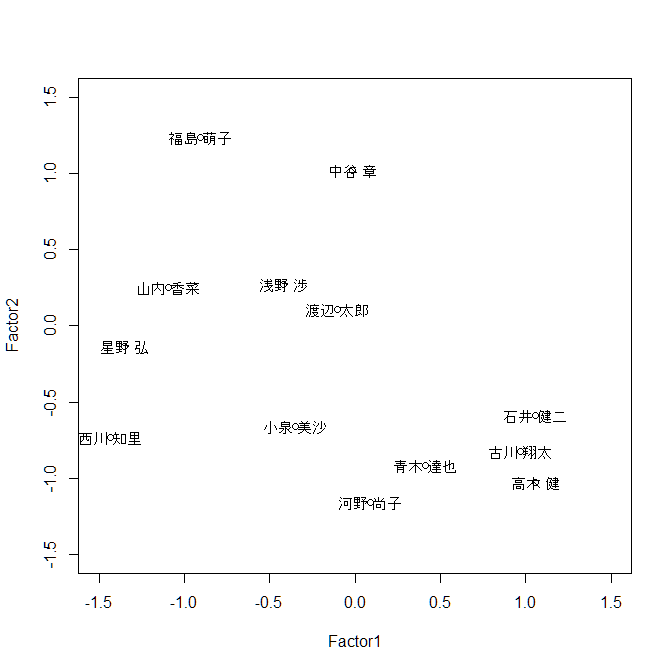
因子得点をグラフで表しましょう．横軸が理系因子，縦軸が文系因子を表しています．グラフから，石井健二や高木健は理系要素が強く，福島萌子や中谷章は文系要素が強いことが読み取れます．

> plot(result2$scores,xlim=c(-1.5,1.5),ylim=c(-1.5,1.5))
> text(result2$scores,labels=score[,1])

因子負荷量と因子得点から独自因子を推定してみましょう．下記のように，標準化されたデータから，因子負荷量と因子得点の積を引いた値（共通因子）が独自因子です．

> common <- result2$scores %*% t(result2$loadings)
> unique <- data - common
> unique
		国語    算数    理科      英語    社会
 [1,] -0.342  0.1731 -0.4883  0.001046 -0.7737
 [2,] -0.297  0.1204 -0.0110  0.000226 -0.4820
 [3,] -0.399  0.1254  0.2676  0.016967  0.9515
 [4,] -0.956  0.3011 -0.9165  0.008880  0.1732
 [5,]  0.625 -0.1329  0.2014 -0.014525  0.4770
 [6,] -0.907 -0.1168  0.3587  0.002645 -0.0575
 [7,]  0.493  0.1272 -0.7461  0.006390 -0.9000
 [8,]  1.019 -0.1885  0.1156 -0.017252  1.1197
 [9,]  0.638 -0.1491 -0.3588 -0.004140  1.8067
[10,]  0.425 -0.0447 -0.0314 -0.004049 -0.5801
[11,] -0.309 -0.1030  0.3794  0.002813  1.3485
[12,] -0.408 -0.2566  0.8781 -0.002201 -0.6764
[13,]  0.611  0.1612 -0.6409  0.003507 -1.3117
[14,]  0.346 -0.1363  0.1413 -0.009367 -0.8871
[15,] -0.538  0.1194  0.8510  0.009060 -0.2082

次に，独自因子の分散が，独自性と一致することを確認しましょう．データの分散から，共通因子の分散を引いた値が，独自性を表します．因子得点は推定値のため，完全には一致しませんが，おおよそ同じ値となることが分かります．

> apply(data,2,var) - apply(common,2,var)
   国語    算数    理科    英語    社会 
0.46521 0.13185 0.40771 0.00991 0.90352 
> result2$uniquenesses
 国語  算数  理科  英語  社会 
0.426 0.080 0.350 0.005 0.898

課題

斜向回転を表すプロマックス法の結果と比べなさい．プロマックス法を適用するには，引数rotationにpromaxを指定します．ソースはchapter14.Rに記述し，因子負荷量と因子得点のグラフの画像ファイルと，chapter14.Rを提出すること．

Top Back

愛知県名古屋市にある椙山女学園大学文化情報学部向研究室の公式サイトです．専門は情報科学であり，人工知能やデータベースなどの技術要素を指導しています．この公式サイトでは，授業で使用している教材を公開すると共に，ベールに包まれた女子大教員のミステリアスな日常を４コマ漫画でお伝えしていきます．サイトに関するご意見やご質問はFacebookまたはTwitterでお問い合わせください．