主成分分析

主成分分析とは

展開演習２の多変量解析と呼ばれる手法を取り上げます． その名が示すように複数の変数を対象に相関や共通性を見つけることが目的となります． 今回は，その中でも，複数の変数を合成して，次元（要素数）を圧縮する主成分分析に注目します． 主成分分析を完全に理解するには数学的な知識が必要となりますが，ここではR言語を利用して直観的に理解することを目指します． このような分析手法は，理解 も重要ですが，使える ことが最も重要です． 対象のデータとして，算数と理科の成績のデータ（CSV形式）を使用するので，事前にダウンロードしておきましょう．

ファイルをダウンロードしたら，read.csv関数を利用して， 変数scoreにデータフレームとして読み込んでおきましょう．

score <- read.csv("score2.csv")

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します． 次に，[ファイル]-[保存]をクリックして，スクリプトを保存します． このとき，ファイル名はchapter13としてください． また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

合成変数

主成分分析では，分散を最大化するような合成変数を求めることが目的となります． 合成変数$f(X)$は，算数の得点を$x_1$， 理科の得点を$x_2$とすると， 下記の式で与えられます．

$f(X) = w_1 \times x_1 + w_2 \times x_2$

それぞれの得点に，重み$w_1，w_2$を掛けただけの簡単な式です． それでは，この重みの意味を考えていましょう． まずは，$w_1=1，w_2=0$の場合はどうでしょうか．

x <- as.matrix(score[,2:3])
w1 <- matrix(c(1,0),nrow=2,ncol=1)
> x %*% w1
	  [,1]
 [1,]   68
 [2,]   78
 [3,]   59
 [4,]   65
 [5,]   74
 [6,]   29
 [7,]   40
 [8,]   71
 [9,]   33
[10,]   53
[11,]   46
[12,]   27
[13,]   57
[14,]   48
[15,]   90

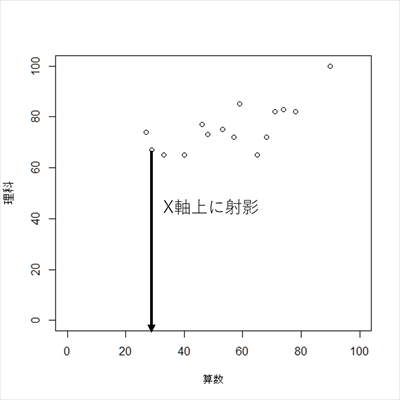
結果は算数の得点となります． これは理科の得点という情報を削って，新しい合成変数を生成したと考えることができます． これは，下記のように，本来は２次元のデータを，算数という１次元の軸に射影したとみなせます．

次に，$w_1=0.5，w_2=0.5$の場合はどうでしょうか．

w2 <- matrix(c(0.5,0.5),nrow=2,ncol=1)
> x %*% w2
	  [,1]
 [1,] 70.0
 [2,] 80.0
 [3,] 72.0
 [4,] 65.0
 [5,] 78.5
 [6,] 48.0
 [7,] 52.5
 [8,] 76.5
 [9,] 49.0
[10,] 64.0
[11,] 61.5
[12,] 50.5
[13,] 64.5
[14,] 60.5
[15,] 95.0

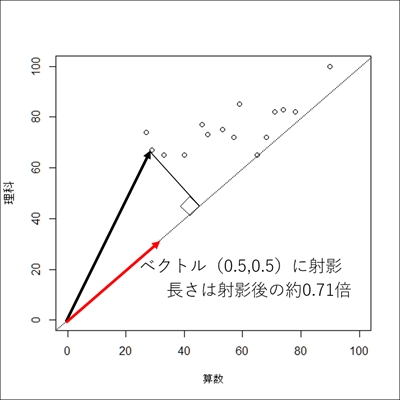
結果は算数と理科の平均値$(x_1 + x_2)/2$を示します． 一方で，この値は，ベクトル$\vec{x}=(x_1,x_2)$と， ベクトル$\vec{w_2} = (0.5,0.5)$の内積と考えることができます． つまり，下図のように，ベクトル$\vec{x}$を， ベクトル$\vec{w_2}$上に射影し， 長さを$||w_2|| \times ||x|| \times \cos(\theta)$とする変換とみなすことができます． このとき，ベクトル$\vec{w_2}$の長さは，

ベクトル$\vec{x}$を射影した長さを，0.71倍したと考えることも可能です．

よって，合成変数とは射影する１次元の軸を回転させることを意味します． では，どのように軸を回転させる方が良いでしょうか． 合成変数は，対象のデータ間の差異を明確にすることが狙いのため， 分散が大きくなるようにベクトル$\vec{w}$を定めます． ここで，上記の合成変数の分散を求めます．

> var(x %*% w1)
		 [,1]
[1,] 353.6952
> var(x %*% w2)
		[,1]
[1,] 174.881

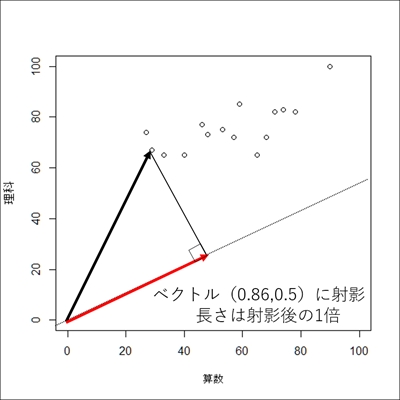
すると，ベクトル$\vec{w_1}$との内積の方が ベクトル$\vec{w_2}$との内積より大きく， 合成変数として適した回転であることがわかります． しかし，$\vec{w}$の値を大きくとれば， それに合わせて，分散が大きくなるため$\vec{w}$はどんな値でも良いというわけではありません． そこで，$||w|| = 1$という条件を加えます． 例えば，軸を30度回転するのであれば，$w = (cos(30),sin(30)) = (0.86,0.5)$と設定します．

w3 <- matrix(c(cos(pi * 1/6),sin(pi * 1/6)),nrow=2,ncol=1)  
> x %*% w3
		   [,1]
 [1,]  94.88973
 [2,] 108.54998
 [3,]  93.59550
 [4,]  88.79165
 [5,] 105.58588
 [6,]  58.61474
 [7,]  67.14102
 [8,] 102.48780
 [9,]  61.07884
[10,]  83.39935
[11,]  78.33717
[12,]  60.38269
[13,]  85.36345
[14,]  78.06922
[15,] 127.94229
[15,] 131.60254
> var(x %*% w3)
		 [,1]
[1,] 398.4386

ベクトル$\vec{w_3}$との内積の分散は約398となり， 他と比べて最も適した回転であることが分かります． 主成分分析は，上記のように軸を回転させて，最も分散が大きくなるベクトル（主成分）を探します． また，その内積（合成）した値を主成分得点と呼び，対象のデータの特徴を表す新しい軸とみなします．

関数を利用した主成分分析

それでは主成分分析を，prcomp 関数を利用して行なってみましょう． この関数を利用すると，対象のデータを標準化（中心を座標(0,0)に移動）することに注意してください．

> result<-prcomp(x)
> result
Standard deviations:
[1] 20.135140  6.234691

Rotation:
			PC1        PC2
算数 -0.9267567  0.3756621
理科 -0.3756621 -0.9267567

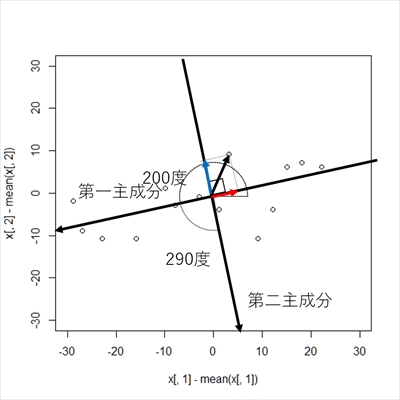
結果を確認すると，$\vec{w}=(-0.93,-0.38)$が 最も分散の大きいベクトルとして導出されました． これは，おおよそ200度の回転を表しています． これを第一主成分と呼びます． このとき，分散の値は$20.14^2=405$です．

また，次点として$\vec{w}=(0.38,-0.93)$が導出されています． これは，おおよそ290度の回転を表しています． 下記のようにベクトル同士の内積は0になることから， 先程のベクトルとは直交する関係にあることが分かります．

> result$rotation[,1]
	  算数       理科
-0.9267567 -0.3756621
> result$rotation[,2]
	  算数       理科
 0.3756621 -0.9267567
> result$rotation[,1] %*% result$rotation[,2]
	 [,1]
[1,]    0

このように，第一主成分と直交するベクトルを第二主成分と呼びます． このとき，分散の値は$6.23^2=39$です． 第一主成分 と 第二主成分 の関係は下図のようになります．

主成分は対象となる変数と同じだけ導出可能ですが，次元を圧縮するという目的から， 第一主成分 と 第二主成分を導出できれば十分なケースが多いです．

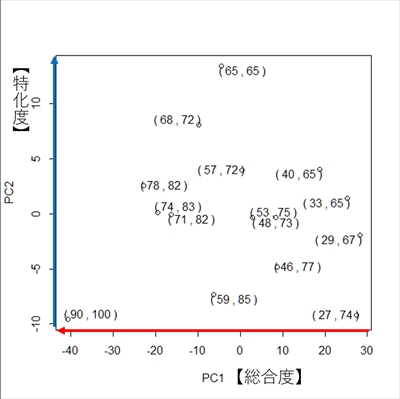
それでは，第一主成分 と 第二主成分 の主成分得点をプロットしてみましょう． 横軸が第一主成分，縦軸が第二主成分を表します．

> result$x
			 PC1         PC2
[1,]  -9.8171320  8.07970897
[2,] -22.8413200  2.56876297
[3,]  -6.3599290 -7.34908707
[4,]  -4.4072272 13.44001958
[5,] -19.5099553  0.13935786
[6,]  28.2046899 -1.93732950
[7,]  18.7616904  4.04846703
[8,] -16.3540231 -0.06087174
[9,]  25.2489873  1.41883232
[10,]   2.9572322 -0.33549266
[11,]   8.6932049 -4.81864078
[12,]  27.4285686 -9.17595062
[13,]   0.3771917  3.94742585
[14,]   8.3423399 -0.36028977
[15,] -40.7243183 -9.60491244

> plot(result$x)
> text(result$x[,1],result$x[,2],labels=paste("(",x[,1],",",x[,2],")"))

この結果から，第一主成分 と 第二主成分 の意味を考えてみましょう． 第一主成分 は，算数と理科の合計が高い人が左，低い人が右に配置されていることから，２科目の総合度 を表していると考えられます． 一方で，第二主成分 は，算数に比べ理科が得意な人が下，算数と理科にあまり差がない人が上に配置されていることから，科目の特化度 を表していると考えられます． このように，主成分分析を適用することで，対象のデータを新たな側面から分析することが可能になります．

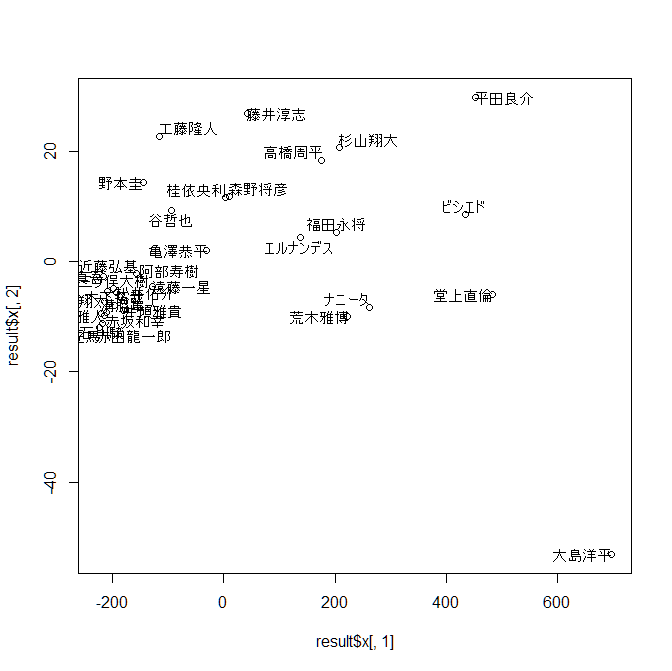
課題

2016年度の中日ドラゴンズの打撃成績のデータ（CSV形式）を対象に主成分分析を適用しなさい． また，第一主成分を横軸，第二主成分を縦軸として主成分得点の散布図を描き，第一主成分と第二主成分の意味を考察すること． ソースはchapter13.Rに記述し，グラフ（散布図）の画像ファイルと，chapter13.R提出すること．