対応のある2群のt検定

0001年1月1日

対応のある2群とは

前回は独立な2群（対応のない2群）の検定を考えました．今回は，対応のある2群 の検定に注目します． 対応のある2群 とは，2つの標本に含まれる対象に，何らかの対応関係があることを意味しています．例えば，下記のように，同じ4人の被験者に対して，2種類の条件下で測定された2群のデータは，「対応のある2群」です．

$条件1: x_1 = \{a,b,c,d\} \\ 条件2: x_2 = \{a',b',c',d'\}$

「独立な2群の検定」には，新しい検定統計量が必要でしたが，「対応のある2群の検定」では，2群のデータの「変化量」に着目することで，標準的なt検定の検定統計量を適用することが可能です．

スクリプトの作成

コードを入力し保存するためのスクリプトを作成しましょう． [ファイル]-[新しいスクリプト]をクリックし，Rエディタを表示します．次に，[ファイル]-[保存]をクリックして，スクリプトを保存します．このとき，ファイル名はchapter12としてください．また，ファイルの保存場所と作業ディレクトリをデスクトップに変更しておきます．

対応のある2群のt検定

それでは，下記の問題について考えていきましょう．

向研究室の学生を対象に実施した情報数学に関するテストの得点は $x_1$ であった．その後，向による熱心な指導を行い，再度，情報数学に関するテストを実施したところ，その得点は $x_2$ となった．指導の前後における得点の平均値に有意な差はあるか．（どちらも同じ母集団からランダムサンプリングした標本だろうか）．

$指導前: x_1 = \{63,75,72,67,71\} \\ 指導後: x_2 = \{82,70,78,81,79\}$

ここでは，指導の前後という対応関係があることから，得点の 変化量 に注目します．変化量は $D = X_2 - X_1$ で与えられます．

$変化量の母集団: D = X_2 - X_1\\ 変化量の標本: d = x_2 - x_1 = \{19,-5,6,14,8\}$

この変化量が，平均 $\hat{\mu}$ ，分散 $\hat{\sigma}^2$ の正規分布に従うと仮定します．

$D \sim N(\hat{\mu},\hat{\sigma}^2)$

すると，この変化量（標本）の平均の分布 $\bar{d}$ は，平均 $\hat{\mu}$ ，分散 $\frac{\hat{\sigma}^2}{n}$ の正規分布に従うことになります．これは，「母集団」と「標本平均の分布」の関係ですね．

$\bar{d} \sim N(\hat{\mu},\frac{\hat{\sigma}^2}{n})$

これを標準化することで，t分布の検定統計量になります．このとき，母集団の標準偏差 $\hat{\sigma}$ は未知のため，代わりに標本の標準偏差 $\sigma_d$ を用いることに注意してください．

$t = \frac{\mu_D - \hat{\mu}}{\sqrt{ \sigma_D^2 / n }}$

母平均 $\hat{\mu}$
標本の平均 $\mu_d$
標本の標準偏差 $\sigma_d$
標本のサンプル数 $n=5$

また，対象が変化量であることから，帰無仮説は $\hat{\mu}=0$ とおくため，上記の式は下記のようになります．随分とスッキリした検定統計量になりました．

$t = \frac{\mu_d}{\sqrt{ \sigma_d^2 / n }}$

それでは，検定の手順に従って，上記の問題を解いていきましょう．まずは，帰無仮説 と 対立仮説 を立てます．

帰無仮説：変化量の母平均は0である $\hat{\mu} = 0$
対立仮説：変化量の母平均は0ではない $\hat{\mu} \neq 0$

次に，検定統計量 と，信頼区間(棄却域) を定めます．今回は，検定統計量は上記のtスコアとし，信頼度には「95%信頼度（5%棄却域）」を用いることにしましょう．

それでは，検定統計量であるtスコアを計算してみましょう．まずは，標本の平均 $\mu_d$ と標準偏差 $\sigma_d$ を求めます．

x1 <- c(63,75,72,67,71)
x2 <- c(82,70,78,81,79)
d <- x2 - x1
mu <- mean(d)
sigma <- sd(d)

> d
[1] 19 -5  6 14  8
> mu
[1] 8.4
> sigma
[1] 9.071935

上記の計算結果を基ににtスコアを求めます．

n = length(d)
t <- mu / sqrt(sigma^2 / n)
> t
[1] 2.070448

最後に，自由度 $n-1=4$ のt分布を利用して，帰無仮説が採択か棄却かを調べましょう． qt関数を用いると，95%信頼度のとき，t<-2.77，また，t>2.77 が棄却域となることが分かります．

> qt(0.025,4)
[1] -2.776445
> qt(0.975,4)
[1] 2.776445

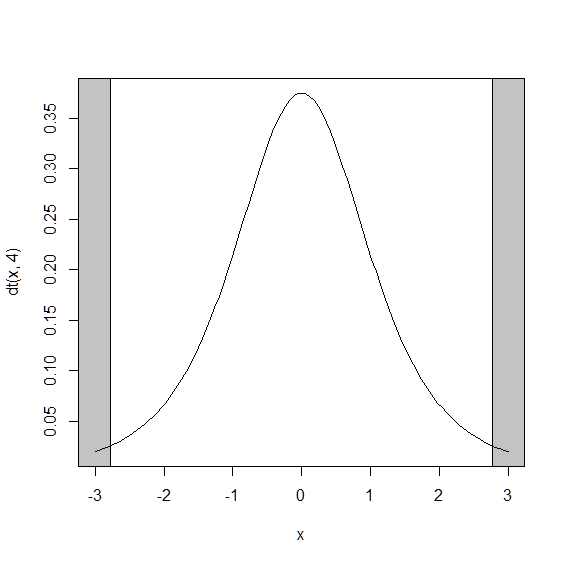
合わせてt分布をグラフにして確認してみましょう．

> curve(dt(x,4),-3,3)
> abline(v=qt(0.025,4))
> abline(v=qt(0.975,4))

上記の結果から，tスコアの2.07は棄却域に含まれないので，帰無仮説「変化量の母平均は0である」が採択されます．これは，指導の前後の得点には有意な差がないということを意味しています．明確に指導の効果があったとは言えないということです．悲しいですね．

関数を利用したt検定

上記の検定はt.test関数でも可能です．引数には「母平均が0である」ことを意味するmu=0を与えます．

> t.test(d,mu=0)

		One Sample t-test

data:  d
t = 2.0704, df = 4, p-value = 0.1072
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -2.864295 19.664295
sample estimates:
mean of x 
	  8.4

tスコアが求めた2.07に一致していることが分かります． p値が0.107（10%）であることから，信頼区間に含まれていることが分かります．また，母集団の平均値の信頼区間は -2.86 から 19.66 となっており，帰無仮説である $\hat{\mu}=0$ が含まれていることが分かります．

課題

指導後の得点が{83,93,75,84,85}だったときのtスコアを求めなさい．また，t検定 を用いて，「95%信頼度（5%棄却域）」のときに，「帰無仮説：変化量の母平均は0である $\hat{\mu} = 0$ 」は棄却されるか調べ，そのときの母集団の平均値の信頼区間も求めなさい．ソースはchapter12.Rに記述して提出すること．